If the Sun Were Suddenly to Explode

In the overview of general relativity contained in the popular book “The Elegant Universe”, Brian Greene discusses the speed with which gravity propagates. He writes

Newton’s theory of gravity claims that if the sun were suddenly to explode, the earth – some 93 million miles away – would instantaneously suffer a departure from its usual elliptical orbit. Even though it would take light from the explosion eight minutes to travel from the sun to the earth, in Newton’s theory knowledge that the sun had exploded would be instantaneously transmitted to the earth through the sudden change in the gravitational force governing its motion.

It might be worth mentioning that Greene’s assertion is based on the premise that the sun would explode in a non-symmetrical way. If, on the other hand, the sun were to explode in a way that maintains its spherical symmetry (i.e., if it expands outward equally in all directions), then the above would not be an accurate description of what Newton’s theory predicts. One of the most fundamental theorems about Newtonian gravity is that a spherical shell of mass exerts (on objects outside the shell) a force of attraction identical to what would be the case if all the mass was concentrated at a point at the center of the shell. Indeed this was the key proposition that enabled Newton to correlate the acceleration of gravity at the Earth’s surface with the acceleration of the Moon in orbit around the Earth. Furthermore, the very fact that Newtonian gravity is instantaneous ensures that the same theorem holds good even if the shell of mass is expanding or contracting. Now, if the Sun – which is more or less spherically symmetrical, and which rotates only very slowly – were to suddenly explode like a supernova, it is at least plausible that it would expand more or less equally in all directions, maintaining it’s spherical symmetry (roughly) about its center of mass, which of course would remain fixed due to conservation of momentum. For such an explosion, Newton’s theory of instantaneous force predicts that there would be no change at all in the gravity exerted on the Earth – at least not until the first wave of matter from the explosion had expanded past the Earth’s orbit.

Interestingly, the same is true in general relativity, because Birkhoff’s theorem proves that there is only one spherically symmetrical exterior solution to the Einstein field equations (namely, the Schwarzschild solution), regardless of whether the source matter is expanding, static, or contracting. Thus we find that Newton’s theory, in which changes in the force of gravity propagate instantaneously, and Einstein’s theory, in which changes in the gravitational field propagate at the speed of light, both predict that the gravitational effect of an exploding Sun (if spherically symmetrical) would not be felt on the Earth until mass-energy from the explosion reached the Earth. In fact, since the flash of electromagnetic energy (including visible light) would represent only a very small gravitational source, we can say that virtually no change in the Sun’s gravity would be felt on the Earth until matter from the exploding Sun passed outside the Earth’s orbit. For a typical supernova explosion the star’s matter expands outward at a speed of about (5)10⁶ meters/second, which is only 1/166 the speed of light. Hence, the first matter from the Sun would take about 22 hours to reach the Earth. During this time, according to both general relativity and Newton’s theory of instantaneous gravity, there would be no appreciable change in the Sun’s gravitational pull on the Earth. This contradicts the book’s claim that in the context of general relativity “we on earth would learn visually of the Sun’s destruction at the same moment that we would feel the gravitational consequences – about eight minutes after it explodes”.

Ironically, if we postulate a propagation delay for Newtonian gravity, we would predict that the exploding Sun’s gravitational pull on the Earth would change much sooner. For example, suppose we postulate that changes in Newton’s gravitational force propagate at the speed of light. On this basis we find that, beginning 8 minutes after the explosion, the effective (delayed) configuration of the Sun’s mass is no longer spherical, and the center of mass of this configuration has moved toward the Earth. The reason for this can be seen in the figure below.

When the Earth is at position E, none of the Sun’s matter has yet reached the Earth, but the gravitational pull of the Sun has already begun to change, because the pull is determined by the configuration of matter on the Earth’s past light cone. The near surface of the Sun is at point A whereas the far surface is at point B, so the effective shape of the Sun (for purposes of determining the gravitational pull on the Earth) is no longer spherical, and the center of the Sun’s mass has now moved in the direction of the Earth.

In summary, if the Sun were suddenly to explode in a spherically symmetrical way, then according to both general relativity and Newton’s theory of instantaneous force, the Sun’s gravitational “pull” on the Earth would not change appreciably until matter from the Sun passed the Earth’s orbit, which would be about 22 hours after the Sun exploded (for a typical supernova explosion). On the other hand, if Newtonian gravity were subject to a propagation delay equal to that of light, then the gravitational effects of the exploding Sun would begin to be felt just 8 minutes after the explosion.

The nearly exact equivalence between general relativity and Newton’s theory of instantaneous gravity sometimes surprises people, because changes in the gravitational field in general relativity propagate at the speed of light, not instantaneously. A similar comparison between the theories can be made with regard to aberration. Laplace determined that the force of Newtonian gravity must be virtually instantaneous (millions of times greater than the speed of light) to avoid unrealistic aberration effects in the planetary orbits, and yet we find (just as in the case of the exploding Sun) that general relativity gives essentially the same results as an instantaneous Newtonian force. The explanation for this is described in the note on aberration of forces and waves .

We should mention that Greene’s description of Newtonian gravity is valid if we assume the Sun explodes in a non-spherical way. Perhaps the Sun’s rotation would break the spherical symmetry, and result in an explosion with only axial symmetry. (It’s hard to imagine the explosion not being at least axially symmetrical.) To make the point clearly, we could consider (say) two metal hemispheres, initially bound together as a sphere, and then blown apart so that the two hemispheres maintain (by internal electromagnetic forces) their individual cohesions as they are propelled in opposite directions. According to Newton’s theory of instantaneous gravity the effect of this changed configuration of matter would be “felt” instantly at all distances. However, it would be difficult to arrange for this to occur for a large gravitating body, and it might be argued that this difficulty is more than just accidental. Nature seems to have a propensity for behaving in such a way that general relativity and instantaneous Newtonian gravity give nearly identical predictions.

Incidentally, later in Greene’s book there is a discussion of force-free motion in a gravitational field, where it states that

objects move through space (spacetime, more precisely) along the shortest possible paths…

Actually the opposite is true: unaccelerated objects move through spacetime along the longest possible paths. The geodesic paths on a manifold are, by definition, those along which the metrical distance is stationary, and in the case of spacetime, with it’s non-positive-definite metric, the proper interval along the worldline of a massive particle following a geodesic path is maximized. This is why the unaccelerated twin in the “twins paradox” undergoes a greater lapse of proper time than his accelerated sibling. Greene devotes a fair amount of text to an explanation of the twins paradox, but if unaccelerated objects really followed the shortest paths through spacetime (as he claims), then his conclusion about which twin ages more ought to be just the opposite of what he says.

One of the more interesting ideas in Greene’s book is introduced in Chapter 10, where he describes the energy of a closed string that is looped all the way around a cylindrical dimension in space. He says that (according to string theory) the energy of the string is the sum of two components – winding energy and vibrational energy – one proportional to the radius R of the cylindrical dimension and the other proportional to 1/R. By exchanging the identities of these two kinds of energy, a universe in which the cylindrical dimension has radius R is (in some sense) indistinguishable from a universe in which it has radius 1/R. This approach is evidently most coherent if all the spatial (but not the temporal?) dimensions are cylindrical – even though the current astronomical evidence actually favors an open universe. As for the possibility of two are more dimensions being spherical (rather than cylindrical), Greene acknowledges that the applicability of these ideas to spherical spaces has not been established. (“Establishing this expectation [of string theorists] is an important goal for further research…”)

From a historical perspective it’s interesting that the Wheeler-Feynman absorber theory of electrodynamics was abandoned partly because the theory could work only in a closed universe, whereas the astronomical evidence suggested (and still does) that the universe is actually open and infinite. This was regarded as a fatal objection to the theory, and yet today we find that string theory similarly requires a spatially closed universe (and may even require cylindrical rather than spherical dimensions), but this is not now regarded as a serious objection to the theory. (Of course, another reason the absorber theory was abandoned was that no one could figure out how to make it compatible with quantum mechanics, whereas string theory apparently does not have this problem.)

Although Greene doesn’t mention it, the inter-changeability between R and 1/R in the laws of physics was discussed long before the advent of string theory. For example, Harry Bateman wrote a paper in 1910 on the general transformations that leave Maxwell’s equations unchanged, and he pointed out that these transformations are precisely the ones that leave the equation

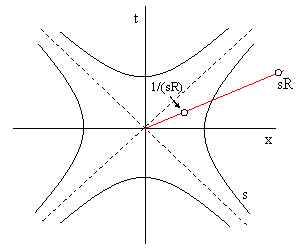
invariant. These are the conformal transformations, which naturally includes the translations, spatial rotations, and Lorentz boosts, but which also include reflections and inversions. In other words, taking any given event in spacetime as the origin, and for any given interval s, we can swap the events at the intervals sR and 1/(sR) along each ray through the origin, as illustrated below.

Maxwell’s equations continue to apply in the transformed spacetime, just as they do in the original spacetime. Felix Klein tried to interest Einstein in this fact, but Einstein didn’t think much of it. He wrote to Klein

I have already had Bateman’s paper in hand but must confess that I cannot quite imagine it possible that any physical meaning  be afforded to substitutions of reciprocal radii… It does seem to me that you are very much over-estimating the value of purely formal approaches… I am convinced that the covariance of Maxwell’s formulas under transformation according to reciprocal radii can have no deeper significance; although this transformation retains the form of the equations, it does not uphold the correlation between coordinates and the measurement results from measuring rods and clocks.

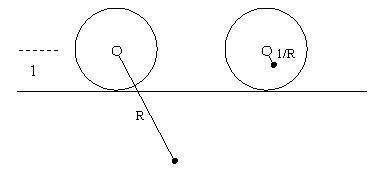
This discussion of the inter-changeability between R and 1/R brings to mind other (admittedly more mundane) circumstances in which physical phenomena don’t distinguish between reciprocal configurations. For example, the note on rocking chairs shows that the equations of motion (though not the energy levels) for two rolling cylinders with pendulum arms having reciprocal radii as shown below are identical.

Reciprocal pairs also arise when dealing with Fourier transforms and uncertainty . If f(x) is a normal density distribution with standard deviation s, then the Fourier transform of f(x) is also a normal distribution, but with standard deviation 1/s. This fact explains the Heisenberg uncertainty relation, because conjugate variables like position and momentum in quantum mechanics are Fourier transforms of each other. We also encounter reciprocal pairs in the study of palindromic polynomials, i.e., polynomials whose coefficients are symmetrical in powers of the variable. For example, the polynomial x⁵ + 7x⁴ – 2x³ – 2x² + 7x + 1 is palindromic. Obviously if R is a root of such a polynomial, then so is 1/R, so such polynomials do not discriminate between these two values. In geometry we often make use of inversion with respect to some specified circle. Each point at a distance R along a ray through the center of the circle is mapped to the point at a distance 1/R along that ray. Inversion transforms circles to circles, and preserves the angles of intersection between curves, i.e., it is a conformal mapping. Inversions (and, more generally, Mobius transformations) also preserve the cross-ratio of any four points.

Of course, the notion of associating the smallest radius of the universe with the largest is not new – and not unique to string theory. In fact, there has long been speculation that the universe might be closed in such a way that the outer and inner radii are literally identified with each other. One way of visualizing this is in terms of a torus as shown below.

According to this model, the universe is cylindrical in the radial direction, and if we depart from a small particle and continue in a straight line we eventually arrive back at the same particle, but we approach that particle from the inside. In this sense the inner and outer radii are literally identified with each other. Interestingly, the complete Schwarzschild solution for the spacetime manifold of a massive particle in general relativity gives an actual instance of precisely this arrangement (at least locally). The exterior manifold can be analytically continued through the “neck” at the Schwarzschild radius r = 2m, so each particle could be regarded as the connection between two separate regions of spacetime, in a multi-holed-torus topology.

The so-called “large number coincidence” has also been taken as the basis for speculation (e.g., Eddington, Dirac) regarding a connection between the largest and smallest spatial magnitudes in the universe, but it isn’t clear if the duality between R and 1/R in string theory accounts for this coincidence in a natural way.

Return to MathPages Main Menu