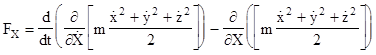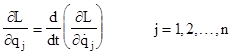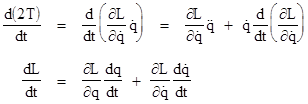Lagrangian and Hamiltonian Mechanics

Lagrange has perhaps done more than any other to give extent and harmony to such deductive researches by showing that the most varied consequences … may be derived from one radical formula, the beauty of the method so suiting the dignity of the results as to make his great work a kind of scientific poem.

                                                                                              W. R. Hamilton

According to Newton's laws, the incremental work dW done by a force f on a particle moving an incremental distance dx, dy, dz in 3-dimensional space is given by the dot product

Now suppose the particle is constrained in such a way that its position has only two degrees of freedom. In other words, there are two generalized position coordinates X and Y such that the position coordinates x, y, and z of the particle are each strictly functions of these two generalized coordinates. We can then define a generalized force F with the components F_X and F_Y such that

The total differentials of x, y, and z are then given by

Substituting these differentials into (1) and collecting terms by dX and dY, we have

Comparing this with (2), we see that the generalized force components are given by

Now, according to Newton's second law of motion, the individual components of force for a particle of mass m are

Substituting into the expression for F_X gives

and similarly for F_Y.  Notice that the first product on the right side can be expanded as

and similarly for the other two products. Since x and X are both strictly functions of t, it follows that partial differentiation with respect to t is the same as total differentiation, and so the order of differentiation in the right-most term of (4) can be reversed (because partial differentiation is commutative). Hence (4) can be written as

Substituting this (and the corresponding expressions for the other two products) into equation (3), we get

Variations in x,y,z and X at constant t are independent of t (since each of these variables is strictly a function of t), so we have

Making these substitutions into (5) gives

Each term now contains an expression of the form r(∂r/∂s), which can also be written as ∂(r²/2)/∂s, so the overall expression can be re-written as

The quantity inside the square brackets is simply the kinetic energy, conventionally denoted by T. Thus the generalized force F_X, and similarly the generalized force F_Y, can be expressed as

These are the Euler-Lagrange equations of motion, which are equivalent to Newton's laws of motion.  (Notice that if X is identified with x in equation (5), then F_X reduces to Newton's expression for f_x, and likewise for the other components.)

If the total energy is conserved, then the work done on the particle must be converted to potential energy, conventionally denoted by V, which must be purely a function of the spatial coordinates x,y,z, or equivalently a function of the generalized configuration coordinates X,Y, and possibly the derivatives of these coordinates, but independent of the time t. (The independence of the Lagrangian with respect to the time coordinate for a process in which energy is conserved is an example of Noether’s theorem, which asserts that any conserved quantity, such as energy, corresponds to a symmetry, i.e., the independence of a system with respect to a particular variable, such as time.) If the potential depends on the derivatives of the position coordinates it is said to be a velocity-dependent potential, as discussed in the note on Gerber’s Gravity. However, most potentials depend only on the position coordinates and not on their derivatives. In that case we have

Comparing this with equation (2), we see that

and therefore the Euler-Lagrange equations (6) for conservative systems can be written as

Rearranging terms, we have

Furthermore, since V is purely a function of the configuration variables, independent of their rates of change, we can just as well substitute (T–V) in place of T on the right sides of these equations, so in terms of the parameter L = T – V these equations can be written simply as

The quantity L is called the Lagrangian. This derivation was carried out for a single particle moving with two degrees of freedom in three-dimensional space, but the same derivation can be applied to collections of any number of particles. For a set of N particles there are 3N configuration coordinates, but the degrees of freedom will often be much less, especially if the particles form rigid bodies. Letting q₁, q₂, .., q_n denote a set of generalized configuration coordinates for a conservative physical system with n degrees of freedom, the equations of motion of the system are

where L is the Lagrangian of the system, i.e., the difference between the kinetic and the potential energies, expressed in terms of the generalized coordinates and their time derivatives. These equations are usually credited jointly to Euler along with Lagrange, because although Lagrange was the first to formulate them specifically as the equations of motion, they were previously derived by Euler as the conditions under which a point passes from one specified place and time to another in such a way that the integral of a given function L with respect to time is stationary. (Roughly speaking, "stationary" means that the value of the integral does not change for incremental variations in the path.) This is a fundamental result in the calculus of variations, and can be applied to fairly arbitrary functions L (i.e., not necessarily the Lagrangian). For a derivation of the Euler conditions, see Relatively Straight.

To illustrate the application of these equations, consider a simple mass-spring system, consisting of a particle of mass m on the x axis attached to the end of a massless spring with spring constant k and null point at x = 0.  For any position x, the spring exerts a force equal to F = kx, and the potential energy is the integral of force with respect to displacement. Similarly the kinetic energy is the integral of the inertial force F = ma with respect to displacement. Thus the kinetic and potential energies of the system are

Therefore the Lagrangian of the system is

The partial derivatives are

Substituting into Lagrange's equation, we get the familiar equation of harmonic motion for a mass-spring system

Of course, this simply expresses Newton's second law, F = ma, for the particle.  It's also equivalent to the fact that the total energy E = T + V is constant, as can be seen by differentiating E with respect to t and then dividing through by dx/dt. 

The equivalence between the Lagrangian equation of motion (for conservative systems) and the conservation of energy is a general consequence of the fact that the kinetic energy of a particle is strictly proportional to the square of the particle's velocity. Of course, in terms of the generalized parameters, it's possible for the kinetic energy to be a function of both q and  (see, for example, Time for a Rocking Chair), but since the transformation dx = (∂x/∂q)dq between x and q is equivalent to dx/dt = (∂x/∂q)dq/dt, it follows that for a fixed configuration the kinetic energy is proportional to the squares of the generalized velocity parameters. Therefore, in general, we have

where we've made use of the fact that the potential energy V (for conservative systems) is independent of .  Now, the total energy is E = T + V = 2T – L, so the conservation of energy can be expressed in the form

The two terms on the right hand side can be expanded as

Substituting into the previous equation and dividing through by  (applying analytic continuation to remove the singularity when  = 0), we see that the conservation of energy implies

which is just Lagrange's equation of motion. Of course, the same derivation applies to any number of particles, and their generalized coordinates.

The correspondence between the conservation of energy and the Lagrangian equations of motion suggests that there might be a convenient variational formulation of mechanics in terms of the total energy E = T + V (as opposed to the Lagrangian L = T – V). Notice that the partial derivative of L with respect to x' is the momentum of the particle. In general, given the Lagrangian, we can define the generalized momenta as

(The partial of V is zero, so it's inclusion and sign in this definition is a matter of convention.) Thus to each generalized configuration coordinate q_j there corresponds a generalized momenta p_j. In our simple mass-spring example with the single generalized coordinate q = x, the total energy H = T + V in terms of these conjugate parameters is

The function H(q,p) is called the Hamiltonian of the system. Taking the partial derivatives of H with respect to p and q, we have

Notice that, in this example, p/m equals q' (essentially by definition, since p = mv), and kq equals –p' (by the equation of motion). In general it can be shown that, for any conservative system with generalized coordinates q_j and the corresponding momenta p_j, if we express the total energy H in terms of the q_j and p_j, then we have

These are Hamilton's equations of motion. Although they are strictly equivalent to Lagrange's and Newton's equations, the equations of Hamilton have proven to be more suitable for adaptation to quantum mechanics. The Lagrangian and Hamiltonian formulations of mechanics are also notable for the fact that they express the laws of mechanics without reference to any particular coordinate system for the configuration space. Of course, in their original forms, they assumed an absolute time coordinate and perfectly rigid bodies, but with suitable restrictions they can be adapted to relativistic mechanics as well.

In quantum mechanics, a pair of conjugate variables q_j, p_j, such as position and momentum, generally do not commute, which means that the operation consisting of a measurement of q_j followed by a measurement of p_j is different than the operation of performing these measurements in the reverse order. This is because the eigenstates corresponding to the respective measurement operators are incompatible. As a result, the system cannot simultaneously have both a definite value of q_j and a definite value of p_j.  See Fourier Transforms and Uncertainty for more on this topic.

Return to MathPages Main Menu