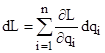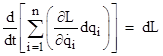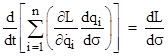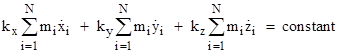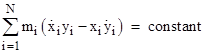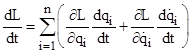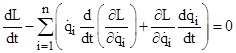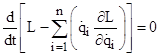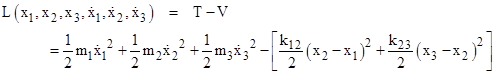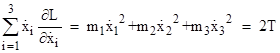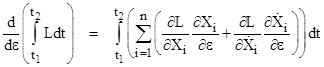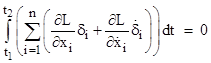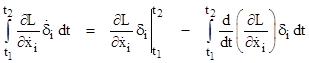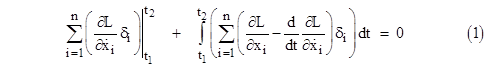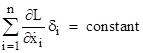Noether’s Theorem

The behavior of a physical system can often be expressed very elegantly in terms of a specific function, called the Lagrangian, of the system variables. The system follows a path through phase space such that the integral of the Lagrangian is stationary. (For more on this, see Lagrangian and Hamiltonian Mechanics.) For a simple system with Lagrangian L of the variables q and  = dq/dt the equation of motion is

This equation signifies that if the quantity on the right hand side is zero (meaning L is symmetrical over q), then the rate of change of the quantity in parentheses on the left side is also zero, so it is a conserved quantity. The same applies to more complicated systems; in general any symmetry of the Lagrangian corresponds to a conserved quantity, and vice versa. Despite the fact that the Euler-Lagrange equation is essentially an explicit statement of this proposition, it seems not to have been discussed and formalized as a theorem until 1915, by Emmy Noether (1882-1935), so it is now called Noether’s Theorem. As an example, the classical Lagrangian of a free particle of mass m is simply L = (1/2)m², which depends only on, not on x, so we have ∂L/∂x = 0, and it follows that  is constant, i.e., momentum is conserved.

More generally, consider a system with n coordinates q₁, q₂, ..., q_n. The Lagrangian L is a function of all n variables and their first derivatives with respect to time. The equations of motion are the n Euler equations, one for each of the variables. The total differential of L with respect to the coordinates q_i is

Multiplying each of the n Euler equations by the respective differential dq_i and adding them together, we get

Thus for any combination of differentials dq_i such that dL = 0, the summation on the left hand side is a constant, i.e., a conserved quantity. Of course, only the proportions between the differentials are significant, not their individual absolute values. Each set of coordinate differential proportions represents a direction in the coordinate space. Letting σ denote a path parameter along a given curve q_i(σ) in coordinate space, we can divide through the above expression by dσ to give in terms of derivatives instead of differentials the formulation

To illustrate, consider a set of N particles with masses m_j and positions x_i, y_i, z_i for i = 1 to N, with a potential energy that depends only on the pair-wise distances between the particles. Clearly that the Lagrangian is unaffected by any fixed displacement of the system, i.e., it is constant along any curve (in phase space) of the form x_i(σ) = k_xσ, y_i(σ) = k_yσ, z_i(σ) = k_zσ for any constants k_x, k_y, k_z. Thus Noether’s Theorem implies

Since the constants k_x, k_y, k_z are arbitrary, it follows that each summation is individually a constant, meaning that momentum is conserved in each of the three coordinate directions, and therefore in every spatial direction. For the same set of particles we could also consider the invariance of the Lagrangian under a fixed rotation (i.e., a re-orientation) of the system about the origin. For each mass with coordinates x,y,z a fixed rotation about the z axis preserves the quantity x² + y² for each point, from which we get xdx + ydy = 0. Thus we can represent the differentials for this symmetry by dx_i = dσ y_i , dy_i = -dσ x_i , and dz_i = 0, so by Noether’s Theorem we have the conserved quantity

This expresses the general conservation of angular momentum about the z axis, and in the same way we can show that the physical symmetry under re-orientations about the x or y axes implies conservation of angular momentum about those axes as well.

In addition to symmetry with respect to spatial displacement and orientation, another important symmetry of all known physical laws is with displacements in time. In this case too the Euler equations identify a conserved quantity. Assuming the Lagrangian L is not an explicit function of time (although the system variables may be), we have the total derivative

The Euler equations for the system enable us to substitute for the partials of L with respect to q_i on the right hand side, and we can express dq_i/dt in dot notation, so we have

Noting that the summand is the derivative with respect to time of a single product, this can also be written as

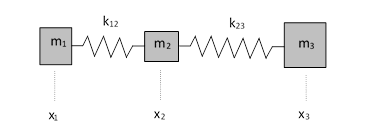
Thus the quantity in square brackets is constant. As an illustration, consider the mass-spring system shown below.

This system has the usual Lagrangian given by kinetic energy T minus potential energy V

We have

Since L = T – V the conserved quantity corresponding to time symmetry is

is the total energy of the system.

For as more formal proof of Noether’s Theorem, and to show how naturally it appears in the derivation of the Euler-Lagrange equation itself, suppose x₁, x₂,…, x_n are the dynamical variables describing the physical state of a system, and each of them is a function of the time t, and suppose the Lagrangian of the system is L(x₁,x₂,…,x_n). The usual way of deriving the equations of motion is to consider a set of perturbed variables

where the functions δ_i(t) are arbitrary variations, and then determine the conditions that must be satisfied in order for the integral of Ldt to be stationary, meaning that the integral is unaffected by an incremental value of the variational parameter ε. To do this we differentiate the integral with respect to ε as follows

Setting this to zero when ε = 0 and therefore X_i = x_i, and substituting for the partials with respect to ε, gives the condition

The second term in each summand can be integrated by parts as

so the preceding equation can be written in the form

At this point we usually focus on disturbing functions that equal zero at the endpoints of the interval from t₁ to t₂, in which case the first term in the above expression is identically zero, and we just need to ensure that the integral vanishes. Since the δ_i functions are independent and arbitrary (between the end points), this requires that each of the summands individually must vanish, so we arrive at the Euler-Lagrange equations of motion

However, Noether made the interesting observation that equation (1) applies to arbitrary disturbing functions, not just those that vanish at the endpoints, provided the function L is unaffected by the disturbances. Furthermore, if the system is evolving in accord with the equations of motion, the integral in (1) vanishes, and the remaining equation implies that the value of the summation is unchanged from t₁ to t₂, so we have the conserved quantity

Noether was primarily an algebraicist (as was her father, Max Noether), but in 1915 she was asked by David Hilbert for help in trying to understand the status of energy conservation in general relativity. As we’ve seen, the conservation of energy in classical physics is closely related to the time-invariance of physical laws, but in general relativity there is not necessarily a global time coordinate, so the classical invariance cannot be invoked to establish the conservation of energy. Nevertheless, if spacetime in the region of interest is regarded as asymptotically flat, it is possible to define a conserved energy. This important aspect of general relativity was greatly clarified by Noether’s Theorem. Subsequently the theorem has found important applications in many branches of physics. For example, in quantum mechanics the phase of the wave function can be incremented without affecting any observables, and this “gauge symmetry” corresponds to the conservation of electric charge. Moreover, Noether’s approach of identifying symmetries with conserved quantities forms the basis of the Standard Model of particle physics.

Return to MathPages Main Menu