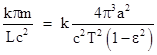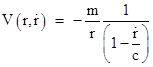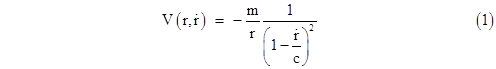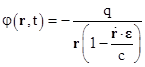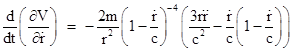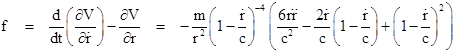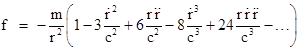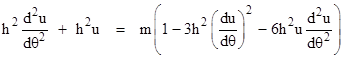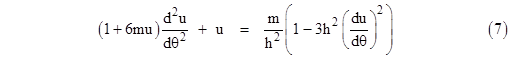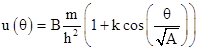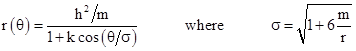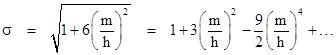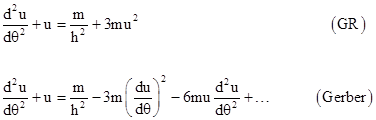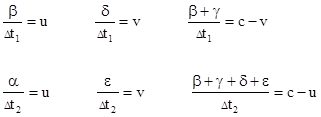Gerber's Gravity

In 1859 the French astronomer LeVerrier announced, based on many years of careful observations and calculations, that the perihelion of the planet Mercury evidently precesses at a slightly faster rate than can be accounted for by Newtonian mechanics given the known distribution of material in the solar system. This discovery led to two different avenues of research. Some people began to search for unknown material in the solar system (possibly even a new planet) that would account for the anomaly in Mercury's orbit within the context of Newton's laws. Others considered possible ways of modifying or re-interpreting Newton's law of gravitation so that it would give Mercury's precession for the currently accepted distribution of matter.

At about this same time, theoretical physicists such as Gauss and Weber were investigating modifications of the Coulomb inverse-square law by introducing a velocity-dependent potential to represent the electromagnetic field, consistent with the finite propagation speed of changes in the field (i.e., the speed of electromagnetic waves). It was found that this same type of law, when applied to gravitation, predicted perihelion advance for the two-body problem on the same order of magnitude as actually observed for Mercury. It became a fairly popular activity in the 1890s for physicists to propose various gravitational potentials based on finite propagation speed in order to account for some or all of Mercury's orbital precession. Oppenheim published a review of these proposals in 1895. The typical result of such proposals is a predicted non-Newtonian advance of orbital perihelia per revolution of kπm/(Lc²) where c is the posited speed of propagation, m is the Sun's mass, L is the semi-latus rectum of the orbit, and k is a constant depending on the precise form of the assumed potential. Of course, by Kepler's law, we can express the mass m of the Sun in terms of the semi-major axis "a" and the angular speed ω of an orbiting planet as m = a³ω². The angular speed can be expressed in terms of the orbital period T (revolutions per second) as ω = 2π/T. In addition, we know from elementary geometry that the semi-latus rectum of an ellipse is L = a(1 – ε²) where ε is the eccentricity. Making these substitutions, the angular precession per orbit can be written in the form

With k = 6 this formula gives the observed non-Newtonian precession for planetary orbits, most notably Mercury's 43 arc seconds per century, so the objective was to find a potential that gives k = 6. Of course, it's trivial to do this in an ad hoc manner, but scientists were attempting to find some rational basis for a potential with the required property. The most straightforward way of incorporating a finite propagation speed into the law of gravity is to simplistically substitute the retarded radial distance for the present distance, which leads to a velocity-dependent potential of the form

but this results in a value of k = 2, so it predicts only 14.1 arc seconds per century for the precession of Mercury's perihelion, one third of the observed value.

In 1898 a German school teacher named Paul Gerber wrote a paper in which he proposed a velocity-dependent potential that gives k = 6. Gerber prepared an expanded version of this paper in 1902, and this expanded paper was subsequently republished in 1917 in the Annalen der Physik at the urging of Ernst Gehrcke, who wished to call attention to Gerber's approach as a possible alternative to Einstein's general relativity. Roseveare gives a brief account of Gerber's ideas in his book on the history of attempts to explain the anomalous advance of Mercury's perihelion, but unfortunately the section of this book devoted to Gerber contains several typographical errors. In addition, Roseveare comments that "the derivations of [Gerber's] force law were not at all clear", so what the book presents is presumably what Roseveare believes is the most plausible line of reasoning. A critique of Roseveare's interpretation is presented below, following which, being dis-satisfied with Roseveare's account, we go back to Gerber's original paper of 1898 and the expanded paper of 1902 (as reprinted in 1917), and give an appraisal of the actual paper. We will find ample support for the complaints of previous reviewers, who characterized Gerber's paper as "unintelligible", "not sound", "incorrect", "wrong through and through", etc. We then conclude with a speculative re-construction of a semi-classical line of reasoning by which it is actually possible to derive Gerber’s potential, albeit in a way that evidently never occurred to Gerber.

To begin, recall that the Newtonian theory of gravity is based on a pure inverse-square force law, i.e., the force per unit mass on a test particle at a distance r from a gravitating body of mass m is f = –m/r². In terms of the gravitational potential V = –m/r the law of gravitation can be written in the form f = –dV/dr. (Note that Roseveare defines potential as positive, whereas we adopt the more usual convention.) In general, for any distribution of masses in space, the gravitational potential at any location is simply the sum of the contributions of the form m/r for each particle of mass m at a distance r from that location. Thus for any distribution of gravitating masses we have a potential field V[x,y,z], and the specific force (i.e., the force per unit mass) on a particle at any given location has the components f_x = –∂V/∂x, f_y = –∂V/∂y, f_z = –∂V/∂z.

The contribution to the Newtonian potential at a given location in space at a given instant due to a mass m is strictly a function of the distance of that mass from the given location at the same instant. In other words, if we let r[t] denote the distance from the given location to the mass particle at the time t, then the contribution of that mass to the gravitational potential V[t] at the given location at the time t is V[t] = –m/r[t]. Thus, Newtonian gravity represents instantaneous action at a distance, because the effect of changing the position of a gravitating mass is "felt" throughout the universe at the instant when the mass moves. Needless to say, for the simple two-body problem this potential gives stable elliptical orbits.

However, suppose the gravitational potential experienced by an object depends not only on the radial distance from the gravitating source but also on the derivative (with respect to time) of that distance. Specifically, suppose the potential has the form

Note that the quantity in parentheses is squared, whereas it appears only to the first power in the straightforward interpretation mentioned previously. This velocity-dependent potential results in elliptical orbits that precess by the same amounts as predicted by general relativity (to the lowest order of approximation), and of course these agree with the observed precession rates for the perihelia of the planets, including Mercury (see below.) The question, then, is whether we can justify the use of this particular velocity-dependent potential rather than the Newtonian potential –m/r.

According to Roseveare's interpretation, Gerber claimed that the form of the potential (1) follows from two assumptions. First, the gravitational potential of a mass source propagate(s) away from the source at a fixed speed (which turns out to be the speed of light) relative to the source, with the strength falling off in proportion to the reciprocal of the distance traveled (as does the amplitude of an electromagnetic wave). Second, the effective potential experienced by an object depends not only on the amplitude of the potential at that location, but also on the relative motion between the object and the potential. According to Roseveare, Gerber argued that each of these assumptions requires us to apply a factor of (1 – r′/c)^–1 to the Newtonian potential, so the combined effective potential is (1).

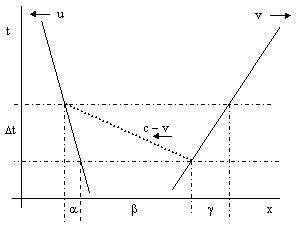
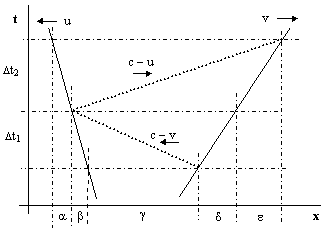
The first factor of 1/(1 – r′/c) is just the usual one, arising from the notion that the potential at any given location and instant depends on the positions of the surrounding masses not at that instant, but at the earlier time such that the potential had time to propagate from the source to the location in question. This is illustrated in the figure below for two point masses moving in opposite direction with speeds u and v.

From the relations

we immediately have

and this represents the ratio of the distance between the masses when the potential was "emitted" to distance between the masses at the present instant. (Needless to say, Gerber was working with pre-relativistic spacetime, so distant simultaneity is unambiguous.) Naturally the relation is reciprocal, so we can represent the potential "flowing" in both directions.

We should comment at this point that it's debatable whether the premises underlying this analysis make any sense. We have assumed that the effective potential is determined by the absolute distance between the masses at the moment the potential was "emitted" (whatever that means), but this is not the same as the distance traveled by the potential. Without invoking instantaneous comminication, it is not clear how the distance at the instant of emission could have this effect. We still need the potential to fall off roughly as 1/r, but the value of "r" is simply given a different interpretation. To address these kinds of problems for models involving "propagating potential" in electrodynamics, C. Neumann proposed a set of premises (1868) that seem to have been adopted by Gerber. (Gerber explicitly mentions Neumann's work in his review of velocity-dependent potential theories.) These premises were summarized by Maxwell in his Treatise on Electricity and Magnetism (1878):

There is the greatest possible difference between the transmission of potential, according to Neumann, and the propagation of light...  A particle sends forth a potential, the value of which depends not only on the charge of the emitting particle, but on the charge of the receiving particle, and on the distance r between the particles at the instant of their emission ... the emitted potential flows to the body on which it acts without the slightest alteration of its original value... the potential as received by the attracted body is identical with, or equal to, the potential which arrives at it...  the velocity of transmission of the potential is not, like that of light, constant relative to the aether or to space, but rather like that of a projectile, constant relative to the velocity of the emitting particle at the instant of emission.

It appears, therefore, that in order to understand the theory of Neumann, we must form a very different representation of the process of the transmission of potential from that to which we have been accustomed in considering the propagation of light.  Whether it can ever be accepted as the 'construirbar Vorstellung' [consistent representation] of the process of transmission, which appeared necessary to Gauss, I cannot say, but I have not myself been able to construct a consistent mental representation of Neumann's theory.

Maxwell was not alone in challenging the intelligibility of the idea of a "flowing" potential (as opposed to a flowing momentum). No one has ever proposed a realistic physical mechanism for such a thing. (Notice that Gerber did not claim to be presenting a mechanistic model; in fact he specifically stated his opinion that no mechanistic model could correctly represent gravity.) This is perhaps not surprising, since potential is not a conserved quantity. For any conserved substance in three-dimensional space the flux density must drop off in proportion to 1/r², whereas potential for an inverse square force drops off as 1/r. In order to reason in terms of a mechanistic flow of a conserved quantity, it would be necessary to work directly with the momentum or force, rather than with the potential. A force field can be modeled as a flow of momentum-carrying particles moving at a fixed speed, as in LaSage's model, but force laws in general do not necessarily have a corresponding potential, i.e., an arbitrary force law is generally not conservative. Also, a retarded force law operating between objects with comparable masses would lead to aberration effects, with the applied force pointing in a direction different from the present direction to the source. This leads to non-physical results. Gerber's 1902 paper contains a fairly lengthy discussion on the question of whether a retarded force or a retarded potential is more intelligible, and Gerber himself seems to have been somewhat ambivalent on the subject. Despite the obvious objections to such a theory, it's interesting to leave these objections aside, just to see how coherently gravity can be modeled along these lines of a temporally propagating potential corresponding to a conservative central force.

Incidentally, one point of confusion in Roseveare's account is that he says dr/dt is the relative velocity at which the source and the test particle "approach each other", which, strictly speaking, implies that the positive sense of this derivative represents decreasing r. However, his later usage of this quantity indicates that a positive value of dr/dt signifies increasing r. Another point of confusion is that he says "if c is the velocity of propagation with respect to the source and Δt is the time taken for the potential to travel from m₁ to m₂, then r = cΔt and the distance traveled by the two masses is r – Δr". Surely he doesn't mean this is the distance traveled by the two masses, but rather it is the distance traveled by the potential.

As for the second factor of (1 – v/c)^–1, Roseveare says "the faster the receiving mass travels, the less potential it receives in unit time". Presumably this is one of the points on which Roseveare felt that Gerber's derivations "were not at all clear". We are given no explanation of what it means for a mass to "receive" potential. We are simply told that there is a potential function, but that the effective potential is something different, depending on the rate at which a body "receives" the actual potential. To say this is "not at all clear" is an understatement. Notice that as v increases, the factor (1 – v/c)^–1 also increases, causing the potential to increase, contradicting the claim that this represents a reduction in the received potential. If we apply the correct factor of (1 – v/c), it would cancel out the retardation factor, leaving just the Newtonian potential m/r.

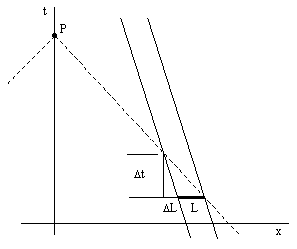
To clarify, it's useful to consider the well-known case of retarded potentials in electro-magnetism. The usual derivation is based on analyzing the potential contributed by a small object possessing some uniform charge density. For the one-dimensional case we can infer the potential at the origin at time t due to a charged object of length L from the diagram shown below.

The potential at the point P depends on how much of its past light cone (represented by the dashed line) contains a charged substance, as well as on the charge density and the distance. (The charged object is assumed to be small enough that the change in distance for the intersection points with the past light cone of P is negligible.) If the object was stationary, the length of time it intersects with the past light cone of P would be proportional to L, but if the object is approaching the origin, the length of time it intersects with the past light cone of P is proportional to L + ΔL. The total charge crossing the past light cone of P is the same, but the charge resides on the light cone for a longer time if the object is approaching P. Hence the static Coulomb potential must be increased by the factor (L + ΔL)/L. From the fact that v = ΔL/Δt and c = (L + ΔL)/Δt, we have (L + ΔL) = cΔt and L = (c–v)Δt, from which we get (L + ΔL)/L = 1/(1 – v/c). More generally, if we let r denote the radial position vector of the charged object, then clearly this potential factor is dependent on just the radial component of dr/dt, so if we let ε denote the unit vector directed from the charged object to the point Q, the Lienard-Wiechert potential is

This bears a superficial resemblance to Gerber's potential (1), and indeed Roseveare evidently thinks that one of Gerber's factors of 1/(1 – v/c) could be justified based on the idea of a retarded potential. The problem is that Gerber's potential does not correctly account for the directional vector ε. This dot product signifies that the retarded potential increases for charges moving toward the location in question, and decreases for charges moving away. The velocity-dependence of Gerber's potential is exactly the opposite. If his dr/dt is positive (meaning the objects are receding from each other), Gerber's potential is increased, and vice versa. Hence, contrary to Roseveare's account, we cannot justify an additional factor of 1/(1 – v/c) in Gerber's potential as an effectivity factor for a retarded potential.

There are other difficulties with Roseveare's interpretation of Gerber's model as well. For example, he suggests that Gerber's potential is "absorbed" by the body on which it acts, but the idea that objects absorb gravitational potential implies that the gravitational field of a mass could be shielded (to some extent) by enclosing it in a thin shell that absorbs all the potential, whereas in fact if we enclose a mass within a shell we increase the total gravitational potential in the surrounding region. The net potential flux emerging from the enclosing shell must equal the sum of the original flux for the enclosed mass plus the flux for the shell. Thus the shell cannot be absorbing any flux. Furthermore, if we are to maintain the idea of absorbed potential, we must follow the implications of this premise for tangential motion. Just as motion directly into the on-coming flow of potential would result in the object "receiving" (or encountering) more potential per unit time, so too would motion perpendicular to the flow. Hence if the effective potential really is proportional to the rate of receipt of actual potential, then the effective potential ought to have terms involving tangential as well as radial velocity. These terms would completely change the character of the solutions for orbital motion.

Overall, it does not seem to me that Roseveare presents a coherent account of the second factor of 1/(1 – r′/c) in Gerber's potential. To determine whether the incoherence is due to a misinterpretation of Gerber or to Gerber himself, we must go back to the source (see below). Of course, in Roseveare's defense, the general consensus among those who have reviewed Gerber's work is that, as von Laue put it, "what Gerber brings forward as physical considerations appears unintelligible". Likewise Bucherer decided that Gerber had justified his potential "by means of false inferences". Interestingly, Seeliger had criticized the notion of absorbed potential which, like Roseveare, he attributed to Gerber, as unintelligible, but he subsequently admitted that a consistent account could have been based on Neumann's conception of effective potential. Indeed from what has been said, it appears that Gerber's premises were essentially identical to Neumann's, but Seeliger insisted that "this is not what Gerber meant". Since Gerber was no longer living in 1917, he couldn't provide any further clarification for the reviewers, who were constrained to base their conclusions solely on the writings themselves. It will be interesting to see (below) what Gerber actually had to say, in his own words.

Before leaving Roseveare, we make a few more miscellaneous observations on his text. In addition to the misleading description of dr/dt as the rate of approach, and the erroneous identification of r – Δr as the distance traveled by the masses, and the erroneous claim that (1 – v/c)^–1 decreases as v increases, Roseveare's discussion of Gerber's theory also contains several other errata: Both of the equations on page 137 are identified as (6.23). Also, equation (6.24) has mis-matched curly and normal parentheses around the last expression. The subsequent equation should presumably be numbered (6.25), but the number is missing. The first term on the right hand side of this equation is given as dv/dt whereas it should be dV/dt. More seriously, there seems to be some confusion in Roseveare's book about the calculation of the precession from a given force law. He says (on page 145) in his discussion of Surdin's potential that "the coefficient [in the equivalent of equation (6)] of the term (r/c)² is the one which determines the magnitude of the perihelion motion". First, this is a typo, since the "r" should obviously be dotted, but more importantly, as will be demonstrated below, the secular precession is actually determined by the coefficient of r d²r/dt². Roseveare notes (correctly) that Surdin's potential gives just 2/3 of Mercury's precession, but he thinks this is because the coefficients of (dr/dt)² in Surdin's potential is -2, compared with -3 for Gerber's. The actual reason is that the coefficient of r d²r/dt² in Surdin is +4, compared with +6 for Gerber's. There also seems to be some confusion in Roseveare's book about his equation (6.31), which he says gives Gerber's potential if we set λ = 2. That's not the case, because the quantity dr/dt appears squared inside the parentheses of (6.31) whereas it is not squared in Gerber's potential (1). The fact that so many errata are packed into this particular section of Roseveare's excellent and useful book is, perhaps, partly due to the difficulty of rationalizing Gerber's reasoning. Before we turn to Gerber's own words, to see if any more rational interpretation can be discerned, it's worthwhile to first review the steps by which the orbital precession is inferred for a given potential, to show that in fact the correct precession is given by (1).

It was stated above that Gerber's velocity-dependent potential gives the same prediction for the precession of orbital perihelia (to the first order for weak fields) as does general relativity. To show this, it's useful to recall some basics of Lagrangian mechanics. (See also Orbits and Perturbations.) The kinetic energy T(x,v) of a particle (or system of particles) in generalized coordinates is a function of both the position x and velocity v. The generalized momentum is equal to p = ∂T/∂v, and Newton's second law is written as

Notice that the first term on the right side is just the rate of change of momentum, whereas the second term is a correction to account for the generalized coordinates. In ordinary Cartesian coordinates the kinetic energy is typically dependent only on the velocity, independent of position, so the second term vanishes.

Now, it is often the case that, from energy considerations, there is a function V(x) of position such that the force F can be expressed purely as the partial derivative

The function V, if it exists, is called the potential. It follows from this and the previous expression that if we define the Lagrangian function L(x,v) = T(x,v) – V(x) then we have

This is formally identical to Euler's equation from the calculus of variations, and as such it signifies that the system moves through phase space in such a way as to extremize the Lagrangian L = T – V. In effect, this is an alternative principle on which to base mechanics. It seems most natural for the effects of velocity to be represented in T, and for the potential function V to be strictly a function of position, but this need not be the case. We might hypothesize that the potential energy is a function not only of position but also of velocity. In that case, if equation (4) is still to be satisfied (in other words, if the behavior of the system is still to extremize the difference between the kinetic and potential energies), the velocity-dependent potential function V(x,v) must satisfy the equation

rather than (3). (Of course, if V is independent of v, then (3) and (5) are equivalent.) This shows that T and V are each individually related to the force(s) on the system by an equation of the same form, but they represent two physically different modes of energy.

On this basis, the proposal of a velocity-dependent potential function (1) corresponds to the proposal of a certain gravitational force law, given by substituting the potential function (1) into equation (5). Making the factor of 1/c explicit, we can write (1) in the form

Then we have the derivatives

and

Thus the force law corresponding to Gerber's potential (assuming the usual Lagrangian equations of motion are satisfied) is

Expanding this in powers of (dr/dt)/c, we get

Since this represents the force per unit mass, directed toward the central gravitating mass m, it is equal to the radial acceleration. To determine the acceleration of a point in the plane, consider a general point z(t) = re^–iθ in the complex plane, where θ is the angular position and r is the radial distance from the origin. Differentiating with respect to time gives

where ω = dθ/dt is the angular velocity. We can rotate these values so that the phase is zero, aligning the purely radial direction with the real axis. Hence the radial and tangential components of the point's acceleration are

There is no tangential force on the orbiting particle (according to Gerber's model), so we have

It follows that the quantity in parentheses is a constant, which we will denote as h = r²ω. Equating the radial acceleration with the radial specific force (up to second order), and reverting to units such that c = 1, we get

If we define u = 1/r, then we have

Therefore, the derivatives of r with respect to time can be expressed in terms of u and its derivatives with respect to the angular position θ as follows

Substituting these expressions for r and its derivatives into (6) and simplifying gives

Re-arranging terms, this can be written in the form

The quantities in parentheses are both nearly equal to unity, because the terms added to or subtracted from 1 are many orders of magnitude less than 1 (for astronomical orbits). Therefore, this equation is essentially a harmonic oscillator of the form

where A and B are taken to be nearly equal to unity. For a suitable choice of reference angle θ, the general solution of this equation can be expressed as

where k is a constant of integration. Notice that B merely scales the solution, so a small periodic variation in B around the value 1 will simply have the effect of superimposing a very slight periodic variation in u, synchronized with the orbital motion. This is not a cumulative effect. It merely alters the precise shape of the orbit (to a negligible extent). Therefore, we can take B = 1. In contrast, if the value of A is consistently greater than 1, even if only by a very small amount, there is a cumulative effect, because the angle θ must increase by more than 2π in order for the system to return to the same radial position. On each revolution this extra angular displacement accumulates, so the spatial path of the orbit undergoes a steady precession.

Reverting back to the parameter r = 1/u, the orbital equation is

If σ were equal to unity, this would be the polar equation of an ellipse with the pole at one focus, and with the constant k signifying the eccentricity and h²/m signifying the semilatus rectum L. The actual value of σ depends on r, but for orbital motion the mean value of r can be expressed in terms of the orbital constants. This is most easily seen for the case of a circular orbit, so the derivatives of u with respect to q are all zero, and equation (7) immediately gives r = h²/m (which of course is equivalent to Kepler's third law, m = r³ω², since h equals mωr²). Substituting for r in the expression for σ, we get

The value of m/h is quite small, so we can take just the first two terms of this expansion. Now, the orbital angle θ must increase by 2πσ in order for the argument of the ellipse to increase by 2π, so the precession per revolution is

This is the same as the first-order non-Newtonian precession predicted by general relativity for weak fields. (See Anomalous Precessions.) The gravitational radius of the Sun is m = 1.475 km and the semilatus rectum of Mercury's orbit is L = (5.544)10⁷ km, so the precession of Mercury's orbit due to this effect (excluding the perturbations of the other planets, etc.) is 0.1034 arc seconds per revolution. Mercury completes 414.93 revolutions per century, so its orbit precesses (due to this effect) by 42.9 arc seconds per century, in excellent agreement with what is observed. This formula also gives values for all other known bodies orbiting the Sun consistent with observation.

We should mention that although general relativity and Gerber's potential predict the same first-order precession (for weak fields), the respective equations of motion are not identical, even at the first non-Newtonian level of approximation. In terms of the parameter u = 1/r the equations of motion are

so the non-Newtonian terms are actually quite different. Of course, any non-Newtonian terms will lead to orbits that fail to close, so there will be some cumulative precession for the two-body problem. It just so happens that the term +3mu² in the GR equation of motion and the term –6mu d²u/dθ² in Gerber's equation of motion both result in a first-order precession of 6πm/L in the slow weak-field limit. Thus Gerber did not in any way anticipate the two-body equation of motion predicted by general relativity, let alone the field equations from which the relativistic equation of motion is derived. This is why the predictions of Gerber’s potential differ significantly from those of general relativity for other phenomena, such as light deflection, which falsifies Gerber’s model.

Nevertheless, we have verified that Gerber's potential (1) does indeed yield the observed non-Newtonian precession for planetary orbits, so we return to the question of the how Gerber arrived at this particular form, and whether it has any consistent representation. We first observe that Gerber presented his ideas not as a way of predicting the non-Newtonian precession of two-body orbits based on the premise that gravity propagates at the speed of light, but rather as a way of evaluating the propagation speed of gravity given the observed precession. Indeed the 1902/1917 paper (which is the fullest account of his ideas) is entitled "On the Speed of Propagation of Gravity". He harkens back to previous analyses (referring to Laplace, et al) based on the absence of aberration effects which seemed to suggest that gravity must propagate, if not instantaneously, then at least ten million times faster than light. On the other hand, he notes that other analyses, similar to his own, suggested a speed of gravity up to 3/5 that of light. He believed the importance of his idea was that it led to the prediction of equality between the speeds of electromagnetic and gravitational disturbances.

The 1902 paper begins with 20 pages of text in which Gerber writes in vague and qualitative terms about the idea that gravity has a finite speed of propagation, and reviews the previous attempts to infer the speed of gravity from observations of the solar system. Following Oppenheim's review article closely, he discusses Laplace, Weber, Reimann, Neumann, Lehmann-Filhes and Hepperger, Clausius, and Lorentz. It is not until Section IV that he begins to present his idea in precise form, giving his "derivation" of the potential (1). First he presents essentially the same argument as given above for the first factor of 1/(1 - r′/c), based on the finite propagation speed c (relative to the emitting body) of the gravitational potential for the interaction between two masses m and m′. Actually he gives this rather trivial derivation three times, once assuming m′ is at rest and m is in motion, once assuming m is at rest and m′ is in motion, and once assuming both are in motion. Of course, the third case subsumes the first two, but he perhaps thought it was more clear to introduce the argument with one of the bodies at rest. In any case, the single factor of 1/(1 - r′/c) was not new or original with Gerber (it was known to give just one third of the observed precession), so we need not dwell on it.

The real point of interest is in Gerber's justification for the second power of 1/(1 – r′/c). Unfortunately, Gerber devotes just two sentences to the introduction of this key element of his model, and neither of those sentences is abundantly clear. This is presented in the section where m′ is assumed to be at rest and m in motion. Prior to this he has arrived at the potential form μ′/(r – Δr + dr) where μ′ denotes the mass m times the gravitational constant, and he subsequently argues that this is essentially equal to μ′/[r(1 – r′/c)], so he has the first factor of 1/(1 - r′/c). Here is the relevant passage along with a (admittedly crude) literal English translation of how he introduces the second factor:

Auberdem aber geht der Zwangszustand nicht wie im Falle der Ruhe von m mit der Geschwindigkeit c, mit der er sich an und fur sich durch den Raum fortpflanzt, sondern noch mit der Geschwindigkeit –dr/dt, die m in C hat, also im ganzen mit der Geschwindigkeit c – dr/dt an m′ voruber.  Die Zeit zur Mitteilung des Potentials an m′ verkurzt sich dadurch im Verhaltnis von c zu c – dr/dt, weshalb das an m′ zur Betatigung kommende Potential, dem gemab sich die Masse m′ zu bewegen anfinge, falls sie im Augenblick frei wurde, gleich u′c/[(r – Δr + dr)(c – dr/dt)] ist.

In addition, however the field goes not from m with the speed of c, with which it propagates relative to m, but adjusted by the speed –dr/dt which m has at point C, thus overall with the speed c – dr/dt toward m′. The time to report the potential to m′ is thereby shortened in the proportion of c to c – dr/dt, which is why the potential arriving at m′, to which the mass m′ would move in response, if it became at the moment free, is u′c/[(r – Δr + dr)(c – dr/dt)].

The new factor that has been introduced here is c/(c – dr/dt), which is the crucial second factor of 1/(1 – r′/c). Recall that our derivation of the first factor of 1/(1 – r′/c) already took into account the posited fact that the field propagates with the fixed speed c relative to the emitting mass, so it is not at all clear why Gerber needs to account for this effect a second time. This can lead to all sorts of speculation about what he might have been thinking. The ambiguity is made worse by the fact that his derivation of the first factor appears somewhat garbled, and it's possible that his quantity (r – Δr + dr) reduces to r(1 – r′/c) only on the assumption that the speed c is absolute, which might have led him to think that he needed to apply another correction to account for the altered speed of propagation. However, the factor of c/(c – r′) does not represent such a correction, so if this is what Gerber was thinking, he was committing a blatant error.

Since the second factor of 1/(1-r′/c) is really the only novel content of Gerber’s thesis (all the rest being just an exercise in freshman claculus), it’s worthwhile to check Gerber’s 1898 paper for any further illumination. Alas, we find that the justification for the crucial second factor given in 1898 consists of just single sentence, which confirms that Gerber surely didn’t grasp its significance. After explaining the first factor, he wrote

Furthermore, the velocity with which the motions are communicated to each other is c – Δr/Δt and therefore the potential, because it takes time to communicate itself to m, turns out to be in the ratio c/(c – Δr/Δt).

Trying to give Gerber the benefit of the doubt, most people (including Seeliger and Roseveare) have decided to interpret this second factor as representing some kind of effectivity factor, arguing that the effective potential applied to m′ depends in some way on the speed at which the potential is impacting (or passing through or being absorbed by) the mass m′. Unfortunately this interpretation doesn't really make any sense, because on this basis (as explained previously in our discussion of the Lienard-Wiechert retarded potential) the effect of a moving source should be just the opposite of what Gerber needs. In other words, if a source is receding it ought to yield less effective potential at a given location than would a stationary source, whereas Gerber needs a factor of 1/(1 – r′/c), which increases for a receding source. Furthermore, this interpretation leads to all the conceptual problems associated with treating potential like a conserved substance discussed previously.

It’s clear that Gerber failed to convey a valid conceptual justification for the form of his potential. Nevertheless, it’s interesting to consider whether there actually exists some coherent framework in which his potential would make sense. I think it’s possible, with some imagination, to construct a nominally viable interpretation. It appears to me that (contrary to Seeliger) Gerber really had adopted the premises of Neumann's electromagnetic theory to which we alluded above. Making some allowances for lack of precision and clarity in Gerber's understanding, we can make sense of many statements in his paper if we view it in the context of Neumann's premises. Of course, Neumann's concepts have been severely criticized, so this wouldn't necessarily have helped Gerber persuade people of the viability of his model, but it's still interesting to examine Gerber's potential in this light.

As we saw in Maxwell's comments previously, the theory of Neumann was criticized for being highly un-mechanistic. Indeed, Neumann himself wrote in 1896 (just two years before Gerber submitted his initial paper) that the conveyance of his effective potential was "a completely transcendental concept, essentially different from the propagation of light or heat". (Interestingly, Gerber also refers to the propagation of "heat and light", and did Lorentz.) Neumann goes on to make the crucial remark (as quoted in Roseveare)

We treat this potential as a stimulus to motion or, to use a better expression, as a command [my emphasis] which is given and emitted by one point and is received and obeyed by the other; we assume the command requires a certain time in order to travel from the place of emission to the place of reception.

It's clear that Neumann really was proposing a highly abstract theory, very different from the mechanistic models that were sought by Maxwell, et al, in the nineteenth century. He conceived of the potential essentially as information being transmitted from place to place, and assumed a finite speed for the propagation of this information. Ironically, Neumann's approach is in many respects consistent with the modern quantum and relativistic representations of phenomena, according to which the interactions between particles are seen not in terms of mechanistic flows of some underlying material substances, but as abstract conveyances along null (light-like) spacetime intervals. In this context, it's worthwhile to recall Maxwell's observation that in Neumann's framework "a particle sends forth a potential, the value of which depends not only on the [mass] of the emitting particle, but on the [mass] of the receiving particle". Now we must ask how the emitting particle knows the mass of the receiving particle. This information must have been conveyed from the receiving particle to the emitting particle. Thus we ought to regard an elementary interaction not as a one-way exchange, but as a two-way round-trip exchange. We can even find some vague support for this interpretation in some of Gerber's introductory verbiage, such as when he says "If for the gravitation between two entities we take into account that the effect transfers itself in reverse [my emphasis] with time delay of first on second, then one finds thereby that the perihelion of a planet is disturbed..." With this in mind, let us revisit our first diagram from above, but this time represent the interaction as a two-way exchange, as shown below.

The exchange of information leading up to the present instant began when the two masses were separated by a distance of γ, and in the mean time they have moved apart due to their respective motions, so their separation at the present instant is α+β+γ+δ+ε. We have the relations

From these we immediately get

and so

We now need the ratio of transmission times in the two directions (reminiscent of Gerber's explanation of his second factor as a ratio of times). Summing pairs of the previous relations gives β+δ = Δt₁(u+v) and α+ε = Δt₂(u+v), so we have

The numerator and denominator can be expressed as

so we arrive at

Thus according to Neumann's (and apparently Gerber's) premises, we find that the effective radial distance for the potential is a factor of (1 – r′/c)² times the present radial distance, and so we have Gerber's potential (1).

It turns out that something similar to the above re-interpretation of Gerber’s proposal was considered long ago. In December of 1916 (the year before Gehrcke re-published Gerber’s paper in the Annalen der Physik), Michele Besso wrote to Einstein

I want to offer a brief survey in the physics colloquium on earlier attempts to explain perihelion motion… I have also thought about Gerber’s idea: It can be presented in a way that makes it appear entirely reasonable: The potential applicable to a moving point has a value corresponding to its location at a time sufficient for an effect to be able first to reach the Sun and to return from it to the planet in that interval. Why Gerber identified this effect specifically with the potential and not with the force, for instance, is naturally not clear. It is not more unreasonable, though, than many other attempts to straighten out novel issues.

However, Besso himself seems to have been confused, because he goes on to say

On the other hand, it appears to me… that although the correct value should come out for Gerber, the opposite sign for the perihelion motion would have to result…

We noted previously that attempts to interpret the second factor of 1/(1 – r′/c) in Gerber’s potential as an “effectivity” do indeed yield the wrong sign, so it’s possible that this is how Besso was interpreting both factors, but this is opposite from the sense that results from a delay interpretation. Nevertheless, despite Besso’s confusion, he did suggest two-way communication as the rationale for the squared factor in Gerber’s potential. (I can find no record of Einstein’s reply to Besso’s letter.)

Of course, Gerber himself never provided any such explanation - and what little he did provide suggests that he didn’t even grasp the significance of the second factor, let alone how to justify it - so the above may just be an example of how with sufficient charity and imagination we can come up with a rational interpretation of almost anything. Still, it should be noted that this approach involves a rather peculiar mixture of finite propagation of information with instantaneous action at a distance (a common criticism of Neumann's approach), because the initial transmission calls for a potential based on the separation between the masses at that instant. On the other hand, it might be possible to eliminate this objection by tracing the information back still further in time, so that we consider the entire sequence of exchanges between the particles, rather than just these two. (It's interesting to compare these exchanges with the interaction terms represented by Feynman diagrams, in which each leg represents a term in the infinite expansion for the interaction. The two legs we have shown would correspond to the dominant terms of the expansion.)

Interestingly, although Gerber is often cited today by proponents of various neo-Newtonian mechanistic theories, his proposed gravitational potential is anything but mechanistic. As mentioned above, Gerber specifically commented on this in his 1902 paper, in which he wrote

Übrigens können die mechanischen theorien das problem der gravitationsgeschwindigkeit überhaupt nicht lösen.  [By the way, mechanical theories cannot solve the problem of the speed of gravitation at all.]

Gerber clearly aligned himself with the more abstract theoretical constructions of Neumann and Lorentz, as opposed to the mechanistic approach of Maxwell. However, it isn't entirely clear that Gerber fully grasped (as Maxwell did, for example) the full implications of Neumann's approach.

By the way, in the introduction to the 1917 re-print of Gerber's paper, Ernst Gehrcke concludes "Whether and how the theory of Gerber can be merged with the well-known electromagnetic equations into a new unified theory is a difficult problem, which still awaits an solution." Indeed, as stressed by Roseveare, although Gerber's potential gives the right perihelia precession rates for the planets, it's prediction for the deflection of electromagnetic waves grazing the Sun is too high by a factor of 3/2, at least assuming a plausible application of Gerber's potential to the propagation of electromagnetic waves. This is discussed fully in the note on Gerber’s Light Deflection, where it is pointed out that, based on the only other plausible application of Gerber’s potential to a ray of light, the deflection it predicts is actually twice the empirical value. So, unless some additional modification is made, Gerber's gravity is experimentally ruled out, regardless of whether a coherent "construirbar Vorstellung" for it can be imagined.

Return to MathPages Main Menu