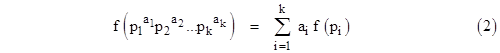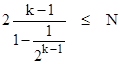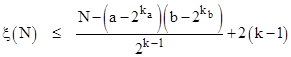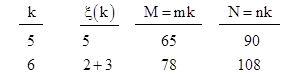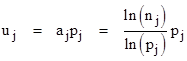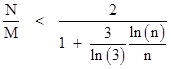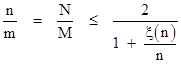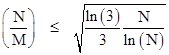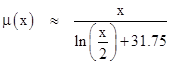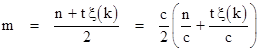Part 1:  Definitions and Basic Propositions

Among real-valued functions f the logarithms f(x) = logb(x) for any positive real base b uniquely possess the Additive Property

for any positive real numbers x and y. If we restrict our attention to the positive integers then clearly the analagous functions must satisfy f(1) = 0 and

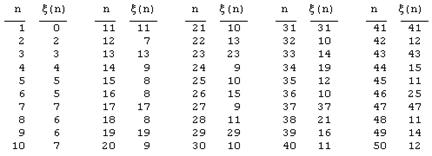
We're free to define the values of  f  for prime arguments arbitrarily. If  we set f(p_i) = p_i  for each prime p_i then f(N) is the sum of the prime factors of N. Hereafter we will denote this function by ξ(N). As an example, ξ(12) = 2 + 2 + 3 = 7. The first several values of this function are shown in the table below.

This note focuses primarily on pairs of distinct integers M,N such that Mξ(M) = Nξ(N). We will often make use of the obvious fact that ξ(N) ≤ N, which is a consequence of the stronger inequality given by the following lemma.

Lemma 1:  If the positive integer N is the product of k primes (not necessarily distinct) then

Also, we have the equality ξ(N) = N  if and only if N equals 4 or a prime. (The left hand relation in the above expression is also an equality for N = 1.)

Proof:  The right-hand relation can be re-written as

Since 2^k ≤ N, this relation follows from

which simpifies to k ≤ 2^k−1, which is true for all integers k (with equality for k = 1 or 2). To prove the left-hand relation of the Lemma, note that, by definition, ξ(1) = 0 and ξ(N) = N if N is a prime, and both of these cases satisfy the Lemma by inspection, so this covers the cases k = 0 and k = 1. If N is composite (i.e., if k > 1) then there are positive integers a,b such that ab = N and ξ(N) = ξ(a) + ξ(b) and 1 < a,b < N. Let the positive integers k, k_a, k_b denote the numbers of prime factors of N, a, b respectively, so we have k = k_a + k_b. If we suppose N is the smallest integer for which the lemma does not hold, then the lemma does hold for the smaller integers a,b, so we have

Therefore,

Re-arranging terms, this gives

Since and , it follows that the product of  and  is a positive number less than N, so the relation is preserved if we omit this product from the above expression, which leads to the relation that was to be proven. ◊

Proposition 1:  If  Mξ(M) = Nξ(N), then gcd(M,N) > 1.

Proof:  Suppose gcd(M,N) = 1. Then N divides ξ(M) and M divides ξ(N). Using Lemma 1 this implies that M ≤ ξ(N) ≤ N and N ≤ ξ(M) ≤ M, which can only be true if M = N, contradicting the assumption that M and N are co-prime. ◊

Proposition 2:  The equality M ξ(M) = N ξ(N) is satisfied in distinct integers M,N if and only if

where m = M/gcd(M,N) and n = N/gcd(M,N).

Proof:  The basic equality can be written as

Dividing both sides by gcd(M,N) and expanding the ξ functions by the Additive Property gives

Solving for ξ(gcd(M,N)) gives the desired result. The inequality ξ(gcd(M,N)) > 1 follows from Proposition 1 and the fact that ξ(k) > 1 for all k > 1 (because k must be divisible by at least one prime ≥ 2). ◊

Discussion:  Proposition 2 shows that to find distinct integers M,N such that M ξ(M) = N ξ(N) we need only find two co-prime integers m and n such that the quantity

is an integer greater than 1. Then M = km and N = kn satisfy the desired equality for any k such that ξ(k) equals Q(m,n). For example, since Q(13,18) = 5, the integers M = 13k and N = 18k constitute a solution pair for any integer k such that ξ(k) = 5. This leads to the two solution pairs:

In general, for any two co-prime positive integers m,n such that Q(m,n) is an integer greater than 1, there is a distinct solution pair corresponding to each prime partition of Q(m,n). We will refer to such pairs m,n as "solution kernels", and adopt the convention m < n. It's clear that the sets of solution pairs for any two distinct kernels are disjoint, because any two integers M,N have a unique gcd.

Table 1 lists all the solution kernels with n < 100. The smallest solution pair is based on the kernel 13,18 with gcd(M,N) = 5, which gives the solution pair 65,90.

To shorten the expressions in the next demonstration we define the function H(n) = nξ(n), in terms of which we state the following lemma.

Lemma 2:  For any positive integers u,v we have

Proof:  The proof is immediate because

which was to be shown. ◊

Proposition 3:  There exist infinitely many pairs of distinct integers M,N such that Mξ(M) = Nξ(N).

Proof:  We prove the assertion by giving an explicit formula for an infinite sequence of such pairs. We claim that for any prime p ≥ 11 the value of

is an integer, and that the integers  M = kp  and  N = k(p+1)  satisfy the condition H(M) = H(N). To prove that k is an integer, we need only show that the exponent of 2 in the preceding expression for k is a non-negative integer. Since p is odd, it follows that p² − H(p+1) − 3 is even, so the exponent is an integer. Also, since p>1 is odd, it follows that p+1 is not a prime, so the maximum value of H(p+1) is 2q(q+2), which occurs when q = (p+1)/2  is a prime. Therefore, the exponent in k is greater than or equal to

which is positive for every prime p ≥ 11. Applying the function H to the integer k as defined above gives

Adding pH(k) + kH(p+1) to both sides, and noting that p² = H(p), we have

By Lemma 2 this proves that

so we have an infinite sequence of solutions, which was to be shown. ◊

Proposition 4:  The co-prime integers m,n with n > 8 constitute a solution kernel if and only if the quantity

is a positive integer.

Proof:  We prove this by showing that, for n > 8, the quantity Q(m,n) is an integer greater than 1 if and only if q(m,n) is a positive integer. The fact that q is an integer iff Q is an integer follows from simple divisibility arguments involving the identity

If q is an integer then n−m divides ξ(m) − ξ(n), which implies that it divides the entire right hand side of this equation, so it also divides the left hand side. Conversely, if Q is an integer then n−m divides the left hand side so it must divide the right hand term m(ξ(m) − ξ(n)), and since m is co-prime to n it is also co-prime to n−m, which proves that n−m must divide ξ(m) − ξ(n).

We now prove that if the integer q is positive and n > 8 then the integer Q is greater than 1. First suppose that (n−m) > 1. It follows that ξ(m) − ξ(n) is greater than 1, because it is divisible by n−m. We also have the identity

Since ξ(m) ≤ m by Lemma 1, this gives the inequality

which proves that Q > 1 if (n−m) > 1. If (n−m) = 1 we must allow the possibility that ξ(m) − ξ(n) = 1. In this case, suppose first that m > ξ(m). It follows that Q = qm − ξ(n) > 1 as required. If, however, m = ξ(m) then m is a prime p, and n = p + 1. The only way for ξ(m) − ξ(n) not to exceed 1 is if ξ(n) = ξ(p+1) = p−1. Since p is odd we can factor a 2 out of p+1 to give ξ(p+1) = ξ((p+1)/2) + 2 = p−1. Therefore, p−3 = ξ((p+1)/2) ≤ (p+1)/2 (by Lemma 1) which gives p ≤ 7 and so n ≤ 8.

Conversely, if Q > 1 it follows immediately from the identity Q + ξ(n) = mq that q is positive. ◊

Corrollary 4.1:  For any solution kernel m,n we have  Q(m,n) ≥ (n-m).

Proof:  Equation 11 gives Q ≥ ξ(m) − ξ(n), and Proposition 3 states that the latter is positive and divisible by (n-m). ◊

Corrollary 4.2:  The relation M + ξ(M) = N + ξ(N) is satisfied if and only if M = mq(m,n) and N = nq(m,n) where {m,n} are a solution kernel or m = 7, n = 8.

Proof:  By Proposition 3 {m,n} constitute a solution kernel if and only if q(m,n) is a positive integer and n > 8. By inspection, the only other case where q(m,n) is a positive integer is when m = 7, n = 8. Therefore, these are precisely the cases when we can set gcd(M,N) = q(m,n) to give the stated solutions. ◊

Lemma 3:  For any positive integer N we have

Proof:  For any quantity U = ξ(N) the value of N can be formed by partitioning U into the sum u₁ + u₂ + ... + u_k, where u_j = a_jp_j for some prime p_j and exponent a_j. Then

Thus u_j contributes a multiplicative factor of  to N. Allowing p_j and a_j to take on any positive real values, we have

Taking the derivative of this with respect to p_j and setting the result equal to zero shows that the minimum occurs at p_j = e (the base of the natural log). The smallest value of p_j/ln(p_j) for integer values of p_j occurs with p = 3. Thus the maximum contribution n_j for each u_j can be no greater than if p_j = 3. Conversely, the smallest value of U for any given N can be no less than if N is a pure power of 3. ◊

Proposition 5:  If Mξ(M) = Nξ(N) with N > M then

where n = N/gcd(M,N).

Proof:  Let m = M/gcd(M,N). Since n − m divides ξ(m) − ξ(n) by Proposition 4, and ξ(m) ≤ m by Lemma 1, we have

and so

Dividing both sides by n gives

which leads to the inequality

We maximize this ratio by minimizing ξ(n)/n. Applying Lemma 3 gives the result. ◊

Discussion:  It's interesting to compare Proposition 5 to an alternative interpretation. Suppose we consider that the maximum value of the ratio N/M occurs when N has the largest value and M has the smallest value consistent with the requirement Mξ(M) = Nξ(N). For any integer n we have

by Lemmas 1 and 3. Thus, based simply on the range of magnitudes of ξ(n), we could not rule out the equality Mξ(M) = Nξ(N) occurring with Mξ(M) = M² and  Nξ(N) = 3N ln(N)/ln(3), which would give the limiting ratio

which is unbounded, in contrast to the upper limit of 2 given by Proposition 5. This illustrates how the divisibility requirements of the discrete integer function impose significant restrictions on the solution pairs that would not be obvious from the point of view of continuous functions.

We've shown (Corrollary 4.1) that if m,n constitute a solution kernel then Q ≥ (n−m). We will refer to solution kernels m,n such that Q = (n−m) as maximal kernels, and to the corresponding solution pairs M,N as maximal solutions.

Proposition 6:  If {m,n} is a maximal kernel with n > m, then m is a prime.

Proof:  A maximal kernel has, by definition,

which can be written as

or

Clearly n must divide the right hand side of this equation, but it is co-prime to m so it must divide m − ξ(m). However, n is greater than m so it is obviously greater than m − ξ(m). Therefore, n divides m − ξ(m) if and only if m − ξ(m) = 0, which by Lemma 1 is true if and only if m is a prime or 4. ◊

Proposition 7:  The integers m,n with n > m and n > 8 constitute a maximal kernel if and only if m is a prime and

Proof:  This follows immediately from equation (33) if we set  m − ξ(m) = 0, which then implies that the term 2m − ξ(n) − n on the left hand side also equals 0. ◊

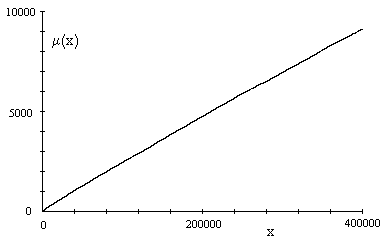
Discussion:  Table 2 lists all the maximal kernels with  n < 2000, and Table 3 lists every 100th maximal solution kernal for n less than 400,000. Letting µ(x) signify the number of maximal kernels with n ≤ x, the figure below shows a plot of μ(x) up to x = 400,000.

It appears from this figure that  μ(x) increases almost linearly with x, similar to the number of primes up to x/2. One possible form is

Corrollary 7.1:  If n,m constitute a maximal kernel then n is composite, and is either a power of 2 or is a product of at least two distinct factors.

Proof:  We have n > m > ξ(n), so n is composite by Lemma 1. Now suppose that n = p^k for some prime p > 2. Then we have

which is obviously not a prime, in contradiction to Proposition 7. Therefore, n cannot be a power of a single prime except 2. ◊

Corrollary 7.2:  If {n,m} constitute a maximal solution kernel and  n = k^t for some positive integers k and t, then  gcd(n,tξ(k)) ≤ 2.

Proof:  Suppose  gcd(n,tξ(k)) = c > 2. Then we have

which is clearly not a prime. Thus, by Proposition 7, the integers {m,n} do not constitute a maximal solution kernel. ◊

Discussion:  As examples of Corrollary 7.2, we have maximal 2-kernels with n equal to the cubes (110)³, (310)³, (470)³, and (494)³. These are all co-prime to 3, as required.

Return to Table of Contents