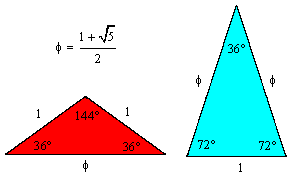Aperiodic Tilings

In a previous note we discussed planar non-periodic tilings with N-fold symmetry, and showed how a suitable set of basis tiles is selected.  One of the examples we considered was the case N = 5 for which the basis tiles consist of the two isosceles triangles

Of course, it's easy to see that these tiles can also tile the plane periodically, i.e., in a pattern that is symmetrical under a set of finite translations.  However, for sets of tiles with more general shapes their ability to tile the plane is not always so obvious.  The question is far from trivial.  In fact, in 1966 Robert Berger proved that no fixed algorithm will determine if a given set of arbitrary tiles will tile the plane.  In a sense this is not surprising, if we consider that geometrical tiling problems often lead to Dipohantine equations, for which there is no general solvability criterion.  (The proof of this fact settled the tenth on David Hilbert's famous list of 23 problems.)  Still, this is a striking illustration of how seemingly simple propositions can be conceptually intractable.  Interestingly, five years before Berger's proof, Hao Wang proved that there would be an algorithm for deciding whether a given set of tiles can tile the plane if every set of tiles that tile the plane also tile the plane periodically.  Hence Berger's proof that no such algorithm exists implies that there must be sets of tiles that can tile the plane only non-periodically.  A tile set with this property is called aperiodic. 

The first known aperiodic set was developed by Berger, and consisted of 20426 tile shapes(!), although he soon reduced this to 104 tiles.  Then in the early 1970's Raphael Robinson devised a relatively simple aperiodic set of just six square-shaped tiles with various notches and extensions on their edges to prevent periodic arrangements, and Roger Penrose found an even simpler set, consisting of just two tiles.  The basic outlines of this set developed by Penrose, with quasi-fivefold symmetry, and how it might be deduced in a more general context were described in the previous note, where we discussed non-periodic tile sets with rotational symmetry of various degrees, and how such tilings can be produced by means of a two-phase process consisting of alternating inflation and subdivision into a fixed set of basis elements.

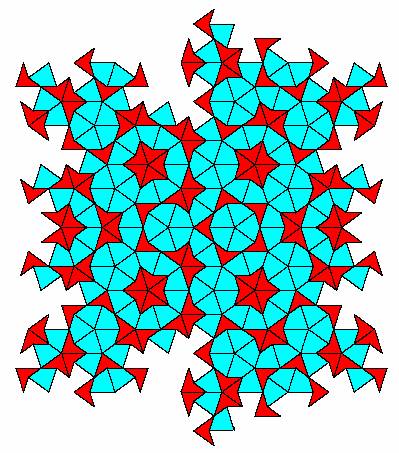
We also saw that at each stage of the construction process there is a great deal of freedom, partly because of the symmetries of the individual tiles under rotation and reflection, and also because the inflated tiles can generally de partitioned into the basis tiles in multiple distinct ways.  In the case of a tiling with fivefold symmetry one fairly arbitrary tiling constructed by this method is shown below.

There is so much freedom of choice in the construction of such tilings that it's natural to take advantage of this freedom by impose additional conditions to create tilings with special properties, such as aperiodicity.  For example, notice in the above tiling that the red tiles join with each other only along their shorter edges and with their bases meeting at a vertex, and the blue tiles join with each other only along their bases or with their with their bases meeting at a vertex (i.e., like the sectors of a polygon).  Also, no more than one red tile is adjoined to any given red tile.  We could impose these conditions as requirements, and thereby limit the freedom of choice in the construction of such tilings.

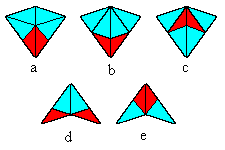
Another approach is to define "meta-tiles" consisting of some fixed combinations of the base tiles, and require that the tiling at each stage be congruent to a tiling modulo these meta-tiles.  This may be best explained with an example.  Notice the figure above contains occurrences of the two tile configurations (among others) shown below.

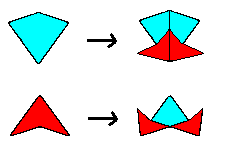
It's traditional to call these shapes "kites" and "darts" respectively.  Each of these consists of two of our base tiles joined together with their "base" edges meeting at a vertex.  We can easily construct inflated versions of these shapes from the basic tiles as shown below.

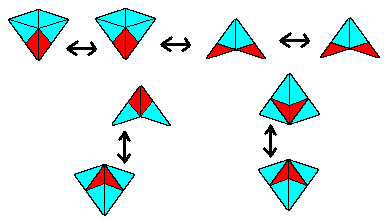
This suggests that it might be possible to tile the plane with these two meta-tile shapes, but not by simple substitution, because although these meta-tiles can be partitioned into the basis tiles, they cannot be partitioned into the meta-tiles.  The meta-darts (d) and (e) each contain two halves of a meta-dart, but not joined in the shape of a meta-dart.  However, we can allow the consolidated meta-tiles on the inflated level to cross the boundaries of the inflated tiles from the previous level, and in fact we can ensure that the inflated level can always be consolidated into meta-tiles by imposing constraints on how the lower-level tiles are adjoined.   The figure below shows the five permissible joins (up to rotations and reflections).

These restrictions can be encoded into the shapes of the tiles by means of notches and spikes as shown below.

It's important to note that these joining restrictions not only ensure that the new tiling can be partitioned into the meta-tiles, but also that the meta-tiles are arranged in such a way that the inflated meta-tiles satisfy the original conditions, so the process can be repeated, just as when working with a set of basis tiles.  It follows that a simple substitution algorithm can be used, provided we augment the partitioning of the inflated meta-tiles as shown below.

Naturally the extensions from neighboring meta-tiles will overlap, but the joining restrictions ensure that the overlapping basis tiles are consistent, so the overlaps are simply redundant.  Beginning with a single kite and iterating these two substitutions with inflation, the result after five stages is shown below.

The joining restrictions are sufficient to prevent the meta-tiles from tiling the plane periodically, whereas we can certainly continue the inflation/partition process described above indefinitely, and therefore tile the entire plane non-periodically.  Thus the meta-tiles (i.e., the kite and dart) constitute an aperiodic set of tiles.  This is the set discovered by Penrose in 1974.  As explained the previously referenced note, the fractions of kites and darts approach the irrational number ϕ for a complete tiling.

It's worth mentioning that a Penrose tiling cannot be constructed simply beginning with a single tile and adding tiles, one at a time, on a fixed scale, based purely on "local" join conditions, making random choices when there is freedom of choice.  If we attempt to proceed in this way, we will soon go wrong and produce a configuration with imperfections, clashes, and/or inconsistencies.  Nevertheless, it appears that some physical substances actually do form into non-periodic quasi-crystals with rotational but not translational symmetry, patterned after this aperiodic tiling.  Such quasi-crystals are typically quite small, and we might suspect that their size is limited by how far they can proceed by simple local growth before engendering a clash with the pattern.  On the other hand, some people (including Penrose) have speculated that there is some kind of non-local process taking place in order to account for the non-local correlations and coherence of the overall "tiling" pattern.  It seems to me the most likely explanation is not quite so exotic: the crystals could grow in essentially the same way that we constructed the figure above, namely, by an alternating two-phase process of inflation and partitioning.  The efficacy of this mode of growth and development of coherent structures is amply demonstrated in biology, where living cells grow and then at some point they split into smaller cells, which then grow (inflate) until they too sub-divide into another generation of cells.  The parallel with our procedure for "growing" aperiodic tilings is extremely close.  In fact, it's not much of an exaggeration to say that every living creature is an aperiodic tiling of cells, produced by a two-phase process of uniform growth alternating with sub-divisions.

Interestingly, the concept of "inflation" has also been raised in cosmology to account for the high degree of coherence between distant parts of the universe that are apparently out of communication with each other.  This seems to be a generic aspect of the physical world, i.e., there is a greater degree of coherence than we would naively expect within a strictly local and fixed-scale framework.  This fact may signify some non-local processes, but it's also possible that the "distant coherence" arises naturally from exponential inflation-partition processes.

Another interesting analogy can be drawn with the Copenhagen interpretation of quantum mechanics, according to which there are two distinct physical processes, (1) the linear evolution of the state vector in accord with the wave equation, and (2) the non-linear "collapse" of the wave function onto a single observed state.  These processes correspond closely with the inflation and partitioning of tile-generation algorithms.  In addition, the distinction between pure states, mixed states, and superpositions in quantum mechanics seems to parallel the relations between basis tiles and meta-tiles in tiling sets.  (Tilings in three and more dimensions have been studied extensively, but could we also conceive of tilings of a Hilbert space?)

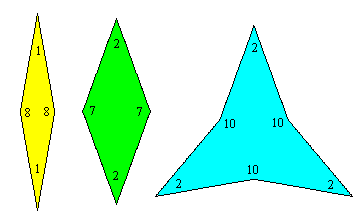
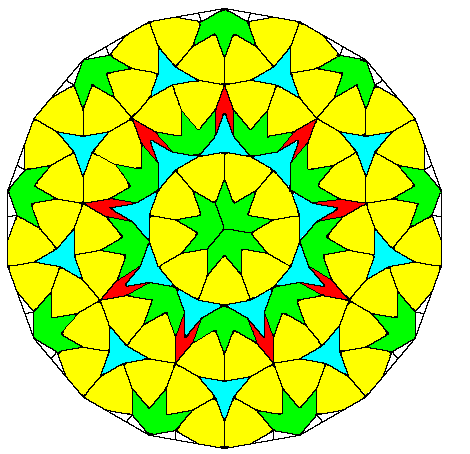
Can other non-periodic tilings with n-fold symmetry serve as the basis for aperiodic tilings?  Consider the non-periodic tiling with 9-fold symmetry described in a previous note.  By consolidating some combinations of the tiles we find that any such tiling can be constructed in terms of the three tiles shown below:

The edge lengths are all identical, and the numbers at the vertices signify multiples of π/9.  The question, then, is whether there is a set of joining restrictions that will prevent (any subset of) these tiles from tiling the plane periodically and yet still allowing them to tile the plane non-periodically.  Needless to say, the joining restrictions must be of a kind that could be enforced locally at each join based on the identities and directions of the edges.  For example, we can impose joining rules that allow yellow tiles to adjoin each other only in a "fan" pattern with a fixed polarity, and likewise the green tiles can adjoin each other only subject to this same condition, and that a green tile can adjoin a blue tile only with the narrow vertex of the green tile meeting an outer vertex of the blue tile.  We also impose the requirement that blue tiles cannot adjoin each other, and that a yellow tile cannot be completely encompassed by just two blue tiles.  With these restrictions we can still apparently tile the plane non-periodically, as shown below.

However, even with the stated joining restrictions, we can tile the plane periodically using two of these three tiles, as shown by the pattern below.

Here we've combined pairs of adjacent yellow tiles into single V-shaped tiles.  If we wish to preclude this periodic pattern we need some additional joining restriction.  Notice that some of the blue tiles in this periodic pattern are encircled by three yellow "V" tiles, all pointing in the same direction.  If we examine the non-periodic pattern shown previously we find that this is never the case, i.e., a blue tile is never encircled by yellow V-shapes all pointing in the same direction.  Each blue tile that is bounded by yellow tiles is either encircled by the three interiors of the three "V"s or else by the sides of three V's, two of which are pointing on one direction and one in the other direction.  So, we propose to add a V-shaped tile to the set of basic tiles, and we impose two new joining rules.  First, no individual yellow tile (of the original type) can adjoin any other yellow tile.  Second, a blue tile cannot be encircled by yellow V-tiles all pointing in the same direction around the perimeter.

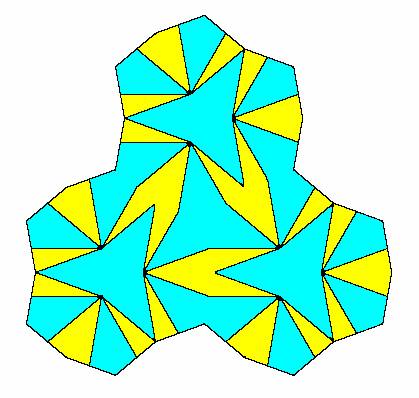
Another way of partitioning the basic non-periodic tiling is in terms of the four types of meta-tiles shown below.

When expressed in terms of these tiles the original non-periodic tiling is as shown below.

Again we seek a set of joining restrictions the allow this non-periodic tiling but that preclude any periodic tiling.  Naturally we must require that the red arrows cannot be "stacked", and that blue tiles do not adjoin each other, and that any given yellow tile can adjoin with a blue tile along only one edge, and so on.  Examining a larger region of the non-periodic tiling would help to determine what restrictions could be imposed while still ensuring that the plane can be tiled non-periodically.

For a more systematic approach to aperiodic tilings, see the note on de Bruijn grids.

Return to MathPages Main Menu