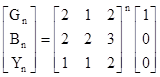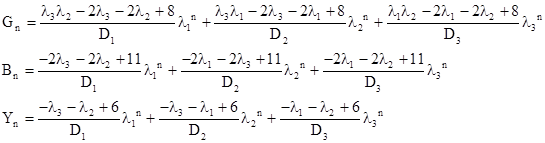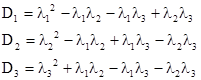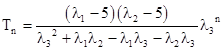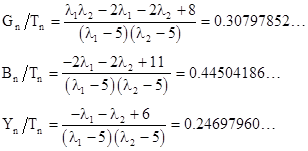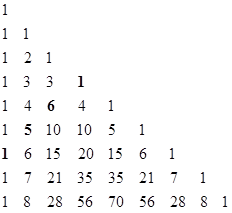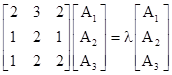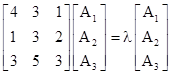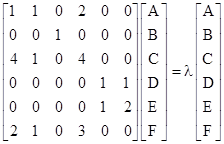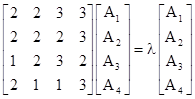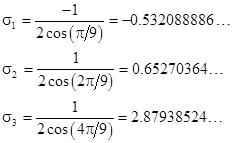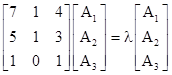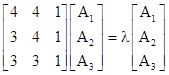Non-Periodic Tilings With N-fold Symmetry

A tiling consists of an arrangement of shapes covering the plane without overlap or gaps. Usually we restrict ourselves to a finite number of shapes and fixed sizes (although we can also consider tiles of geometrically decreasing and increasing sizes). The simplest and, in some sense, most natural tilings are periodic, in the sense that they consist of a meta-tiling of duplicated regions under translation. Three common periodic tilings, one consisting of triangles, one of squares, and one of hexagons, are illustrated below.

These tilings have rotational periodicities as well, and since they are rotationally periodic about one point, and they are translationally periodic, it follows that they are rotationally periodic about infinitely many points, as distinct from, say, a sliced pie, which has rotational symmetry only about the central point. It's trivial to define patterns with rotational symmetry about a single point, but if we also require translational symmetry, it can be shown that the only possible rotational symmetries are of order 2, 3, 4, and 6. This is called the crystallographic restriction.

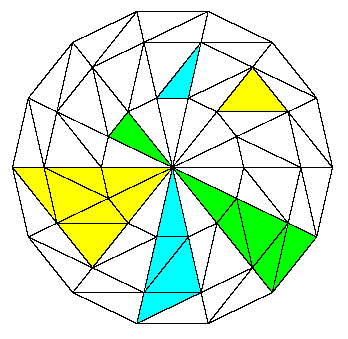
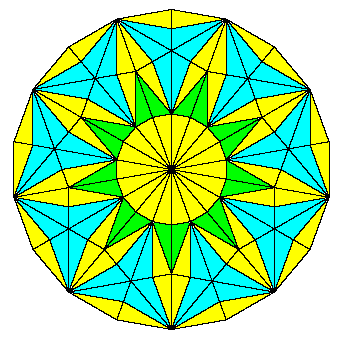
It's also possible to tile the plane non-periodically. The best-known non-periodic tilings are the Penrose tilings based on the pentagon and the golden ratio. (These tiles also have the property that they can tile the plane only non-periodically, not periodically. Such tilings are called "aperiodic". Typically this is achieved by imposing edge-matching conditions on a set of tiles to prevent them from being able to tile periodically.) It's interesting to consider other non-periodic tilings. The figure below illustrates a tiling based on the septagon (7-sided regular polygon), although it actually produces a 14-way symmetry (at least about the central point).

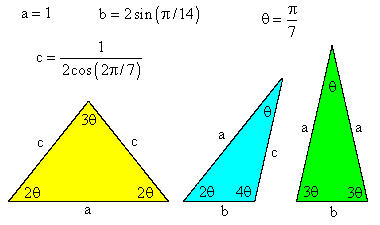
The 14-sided polygon is tiled with just the three types of tiles shown below:

The key to this tiling is the fact that these three basic tiles can be combined to produce scaled-up copies of themselves. The scale factor is a/b = 2.24697... Alternatively, these tiles can be sub-divided into scaled-down versions of themselves. Consequently, beginning with the 14-sided tiled polygon shown above, we can "inflate" the figure by a factor of 2.24697...  This is done by scaling up the entire figure by this factor, and then sub-dividing each expanded tile into tiles of the original size. Obviously we can continue this process indefinitely, so this proves that we can tile the entire plane with this 14-way symmetry using just these three tiles. The result of the first inflation step is shown below.

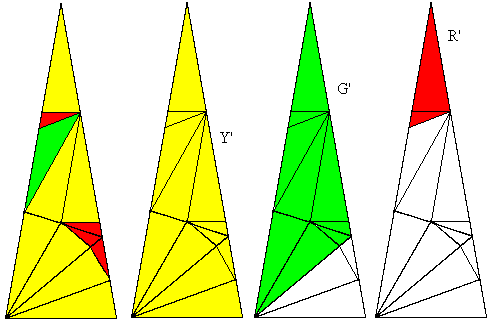
We will call the tiles with edge lengths (a,a,b) the "G" tiles (for Green), and the tiles with edge lengths (a,b,c) will be called "B" tiles (for Blue), and the tiles with edge lengths (a,a,c) will be called Y tiles (for Yellow). We can start with an initial 14-gon tiling consisting of just 14 G tiles, but since the overall figure has perfect 14-way symmetry, we need consider only one of these slices, consisting of just a single G tile. Thereafter, with each inflation step, each G tile is partitioned into 2 G tiles, 2 B tiles, and 1 Y tile. Likewise, each B tile is partitioned into 1 G tile, 2 B tiles, and 1 Y tile. Also, each Y tile is partitioned into 2 G tiles, 3 B tiles, and 2 Y tiles. Thus if we let G_n, B_n, and Y_n denote the numbers of tiles of the respective types contained in the original slice after the nth inflation step, we have the relations

The determinant of the coefficient array is 1, and the characteristic polynomial is

which has the roots

We also have the recurrence relation for the number of G tiles after the nth inflation

and likewise for the numbers of B and Y tiles. We can also give the number of the different kinds of tiles explicitly in terms of the characteristic roots as follows.

where

Interestingly, the coefficients of the expressions for B_n and Y_n are just permutations of each other (with opposite signs). The values of the characteristic roots are λ₁ = 0.307978..., λ₂ = 0.643104..., and λ₃ = 5.048917..., so as n increases the terms involving λ₁ and λ₂ go to zero and only the term involving λ₃ is significant. As a result, the numbers of tiles of the three types are asymptotic to

and the total number of tiles goes to

From this we can determine the asymptotic proportions of the three kinds of tiles. We have

Notice that B_n/T_n equals the ratio of edge lengths b/a, which equals 2sin(π/14). We can also see that G_n/T_n equals 1 + a/b = λ₁, and Y_n/T_n equals a/b – 2 = a/c – 1. In addition, we have Y_n/G_n = c/a. Since the characteristic polynomial is irreducible, we know the roots are irrational, so the asymptotic proportions of the tiles are also irrational, which implies that the tiling is non-periodic. (For a periodic tiling, the entire plane is covered with copies of some finite region, in which the proportions of different tile types is obviously rational, and this is the asymptotic proportion as well.)

Incidentally, although the characteristic polynomial (1) is irreducible over the rationals, if we put λ = σ² we have the factorization

In terms of the edge lengths a,b,c of our tiles, we notice that the roots of the right hand factor are c/a, –a/b, and b/a – 1, and the roots of the left hand factor are a/b, –c/a, and c/a + 1. is a root of the left hand factor, and c/a is a root of the right hand factor. Thus it's not surprising that there are numerous relations between the edge lengths and the characteristic roots, such as

We also have several relations between the edge lengths themselves, such as

The left hand relation implies that c/a is the sum of the infinite geometric series in b/a, whereas the right-most relation signifies that b is half the harmonic mean of a and c.

The tiling is self-similar at each inflation stage, in the sense that the pattern on the existing region is replicated once the tiling has been expanded and the larger tiles have been partitioned back into tiles of the original size. Therefore, it is possible in principle to construct the entire tiling incrementally by adding tiles of a fixed size to the outer edge, one at a time. However, the correct pattern that must be followed in order to continuing replicating the tiling on larger and larger scales becomes increasingly complex.

One notable feature of this tiling is that the vertices of the adjoining tiles don't appear to always be aligned. In other words, it appears that the vertex of one tile contacts another tile at some intermediate point on its edge. However, the distinction between edge points and vertices is somewhat conventional, because any point on an edge can be regarded as a vertex between two edges making an angle of π.

The relations exhibited by this non-periodic tiling have analogs for tilings with other rotational symmetries. In general, to find a non-periodic tiling with n-way symmetry, we need an irreducible polynomial P(x) of degree (n–1)/2 with integer coefficients such that P(x²) factors into two polynomials of degree (n–1)/2. This is motivated by the fact that we need to be able to combine areas as well as edge lengths rationally, so we need polynomials whose roots are the squares of the roots of another related polynomial. A suitable family of polynomials is given by diagonal slices through Pascal's triangle

For the seven-fold symmetry of the tiling described above, we took the polynomial of degree (7–1)/2 = 3 with the coefficients 1, -6, 5, -1 from a diagonal of this triangle. All the polynomials formed in this way have the property that they factor when a squared variable is substituted for the original variable. Also, the fundamental roots (with alternating signs for the coefficients) are all positive and real.

To illustrate how this enables us to find non-periodic tilings with n-fold symmetry for a given n, let's take the simple case n = 5. Rather than just conducting an exhaustive search of all the possibilities for a tiling with 5-fold symmetry, it's illuminating to follow a definite procedure which, according to our method, is based on the polynomial of degree (5–1)/2 = 2 with coefficients from a diagonal of Pascal's triangle, namely, x² – 3x + 1, which factors as (u² – u – 1)(u² + u – 1) where x = u². This will lead to two triangles that can be "inflated" rationally. The polynomial has the roots 2.618... and 0.381... and, as in the case of the 7-fold tiling, the inflation factor will be the square root of the largest root, which gives 1.618..., i.e., the golden ratio ϕ. In addition, the square root is 0.618..., i.e., 1/ϕ, which will equal a ratio of edge lengths of the two tiles.

We can also infer the numbers of each of the two kinds of tiles that will be combined to give the inflated tiles. We seek positive integers n₁₁, n₁₂, n₂₁, n₂₂ such that λA₁ = n₁₁A₁ + n₁₂ A₂ and λA₂ = n₂₁ A₁ + n₂₂ A₂. This eigenvalue problem has the characteristic equation given by our Pascal polynomial, i.e., λ² – 3λ + 1, so we know the integers satisfy the conditions n₁₁ + n₂₂ = 3 and n₁₁ n₂₂ – n₁₂ n₂₁ = 1. From this it follows that n₁₁ = 1, n₂₂ = 2, n₁₂ = 1, and n₂₁ = 1. Thus we know that the inflated version of one of the tiles is composed of one each of the two base tiles, whereas the inflated version of the other tile is composed of two of itself and one of the other. Obviously the second must be the larger of the two.

So, we begin with a slice of a 2n-gon, i.e., an isosceles triangle with peak angle of π/5, and then we partition this triangle into two parts, one of which is similar to the original slice, and the other of which has edge lengths in the ratio of ϕ to 1. Also, we know the ratio of the areas of these two tiles (namely, ϕ²). One partitioning that meets these conditions is shown below for each of the ten slices of a decagon.

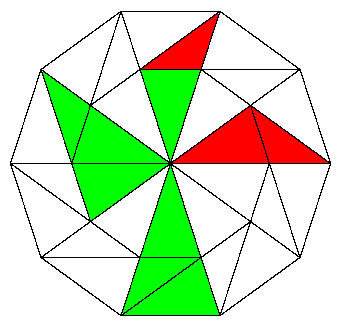
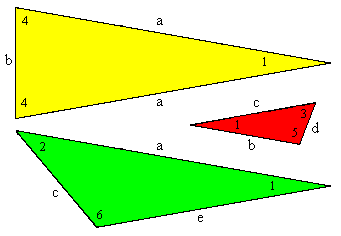
By construction we know two copies of the larger (green) tile combined with one copy of the smaller (red) tile produce an inflated copy of the larger tile. In fact, this can be done in two distinct ways, as shown in the figure above. By inflation we can expand this pattern indefinitely.

Incidentally, if we carry out this procedure for a 3-fold symmetric tiling, we would be partitioning a slice of a hexagon, i.e., and equilateral triangle, into one part. The characteristic polynomial is x – 1, so the inflation scale factor is just 1. This is a degenerate case.

For a less trivial illustration of this general method, we will derive the non-periodic tiling with 7-fold symmetry discussed previously. Referring again to Pascal's triangle, we have the characteristic polynomials

where x = u². From this we immediately know our inflation scale factor is √λ=2.249… where λ is the largest characteristic value. We seek (7–1)/2 = 3 triangular tiles that partition a slice of a 14-gon, one of which is similar to this slice, such that some combination of these parts produces inflated versions of the same parts. The area equations are λA₁ = n₁₁ A₁ + n₁₂ A₂ + n₁₃ A₃, and similarly for the other two areas. The characteristic equation of the coefficient array for this set of equations must be our Pascal polynomial, so we have the trace condition n₁₁ + n₂₂ + n₃₃ = 6 in positive integers. The only possibilities are 1+1+4, 1+2+3, and 2+2+2. The most uniform is 2+2+2, so we take this option, and then the conditions on the remaining coefficients are

For the second condition we can exclude the partitions 1+7 and 2+5, because they would violate the first condition. Thus the only possibility is 3+4, which implies one of the coefficients is 3, so the first partition of 7 must be 2+2+3. Setting n₁₂=3, we must have n₂₁ = n₃₁ = n₂₃ = 1 and n₁₃ = n₃₂ = 2, so our area equation is

Thus we know how many of each type of tile appears in the inflated version of each tile, in agreement with what we saw earlier for the 7-fold symmetric tiling. The eigenvector of this equation with the eigenvalue λ = 5.058... then gives the ratios of the area of the three tile types. Combining this with the known inflation scale factor and the edge length ratios given by the square roots of the roots of the characteristic polynomial, we can partition a slice of a regular 14-gon into three triangles to satisfy these requirements, and arrive at the tiling discussed previously.

Incidentally, such solutions are not unique. As an example, I've just learned that Ludwig Danzer is credited with a non-periodic tiling with 7-fold symmetry based on the same tile shapes as for the 7-fold tiling described above, but they are arranged differently. It appears that the condition of "vertex to vertex" mating of the edges was imposed as an additional constraint. In any case, the area equation of the Danzer tiling is

which has the characteristic polynomial

Notice that if we replace u with u + 1 in the first factor and with u – 1 in the second factor we get the two factors of our previous characteristic polynomial. The opposite substitutions give u³ ± 7u² + 14u ± 7.

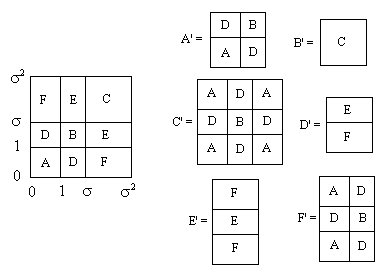
In general we can find a non-periodic tiling corresponding to any given polynomial. This is particularly easy if we use rectangular tiles. To illustrate, consider the polynomial f(x) = x³ – x² – x – 1, and let σ = 1.839286755... denote the largest real root. Thus we have the relations σ³ = σ² + σ + 1. We can now define a rectangular grid as shown on the left below, based on the powers of σ.

There are six distinct tile shapes, denoted by A through F, and the inflated versions of each tile (scaled up by a linear factor of σ) can be composed of copies of the original tiles as indicated by the right hand figures above. The column and row arrangements are chosen so that no tile shares a common edge with another tile of the same type. Letting each tile symbol denote the area of the tile, the area equation is

so the characteristic polynomial is

Setting λ = σ², the first factor on the right splits into the two cubics

consistent with the fact that the linear scale factor σ is a root of x³ = x² + x + 1.

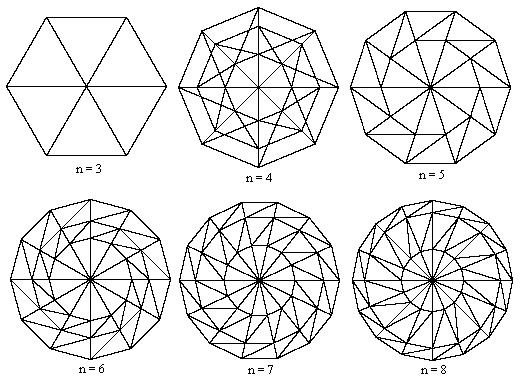
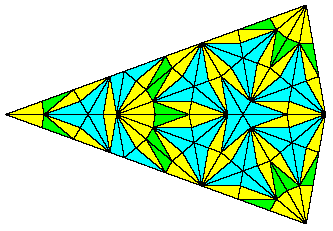
Clearly it's more challenging to find non-rectangular tilings. We saw previously how to determine tilings with n-fold rotational symmetry for n=5 or n=7. These were both based on slices of a 2n-gon, placing a tile similar to the overall slice at the end of the slice as well as at the hub. The results of carrying out this same arrangement for values of n from 3 to 8 are shown below.

The cases of n = 3 (trivially), n=5, and n=7 exhibit special resonances that lead to successful tilings under this scheme.

We can go on to consider the case of 9-fold symmetry, based on the characteristic quartic x⁴ – 10x³ + 15x² – 7x + 1. One area equation that maps to this quartic is

where λ is the largest eigenvalue (the square of the inflation scale factor). However, since 9 is not a prime, the characteristic polynomial is factorable over the rationals, with the factorization (x – 1)(x³ – 9x² + 6x – 1). Setting u² = x, these factors split further as (u–1)(u+1) and (u³ – 3u² + 1) (u³ + 3u² – 1). It's more convenient to take advantage of this factorability, excluding the unit eigenvalues (which correspond to the trivial 3-fold symmetry) and focus on just the cubic. The first "u" cubic has the roots

and the roots of the second "u" cubic are the negations of these. We can then select a trace for the area matrix such as 7+1+1 and then determine the remaining coefficients of the matrix, leading to the area equation

with the largest eigenvalue λ = 1/[4cos(4π/9)²] = 8.2908603... corresponding to the linear scale factor of σ = σ₃ as given above. Thus the inflated version of the tile with area A₁ is to be composed of 7 copies of the tile with area A₁, 1 copy of the tile with area A₂, and 4 copies of the tile with area A₃. Likewise we can read the compositions of the other tile area from this equation.

A set of tiles that satisfies these conditions is illustrated below. This figure shows four slices of a regular 18-sided polygon. The first slice shows one way of partitioning such a slice into copies of three smaller shapes. The three shapes are colored yellow, green, and red, and their individual areas A₁, A₂, and A₃ comprise an eigenvector of the area equation. The long edge of the overall slice is σ times the short edge, so the inflated version of the yellow tile, labeled as Y', is simply an entire slice of the 18-gon, and we can verify that it consists of 7 yellow tiles, 1 green tile, and 4 red tiles. The inflated version of the green tile is labeled as G', and is composed of 5 yellow, 1 green, and 3 red tiles. Lastly, the inflated red tile, labeled as R', is composed of 1 yellow and one red tile.

Thus we can create an infinite non-periodic tiling with 9-fold symmetry from just the three tiles shown below.

The integers inside the tiles signify the interior vertex angles in multiples of π/9. For a more uniform set of tiles, we can partition the yellow and green tiles, and arrive at the 9-fold symmetrical tiling as indicated in the figure below.

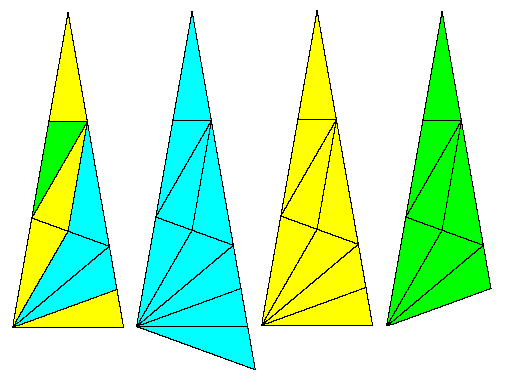
The slice of a regular 18-gon on the left shows the basic partitioning into 3 blue, 4 yellow, and 1 green tile, and the three figures on the right indicate the inflated versions of those tiles. Naturally the area equation for this non-periodic tiling

still has the correct characteristic polynomial, i.e., x³ – 9x² + 6x – 1. Arranging 18 slices such that all tiles meet edge-to-edge and vertex-to-vertex gives the pattern shown below.

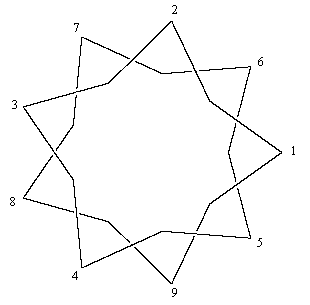
Notice the fundamental 9-step symmetry of the dominant edge loops, as emphasized by the double-covering cycle of the type illustrated in the figure below.

If we carry out the first inflation step, replacing each expanded tile with its composition tiles, again requiring that tiles meet at vertices only, we get the pattern indicated by one-ninth of the 18-gon shown below.

Clearly the requirement for vertex-to-vertex joining implies that the blue tiles will always appear in the six-tile cluster, so we could replace the blue tiles with a single tile in the shape of this cluster. It's also worth noting that the yellow tiles join to other yellow tiles only along it's "end" or else as slices with a common hub, never in the opposite direction. With this restriction, it cannot tile the plane periodically. The green tiles sometimes meet parallel and sometimes anti-parallel, so they do form a parallelegram, but they never meet "end to end", so they too can be prevented from tiling the plane periodically. Moreover, we can always re-arrange a green and yello tile so that the green tiles meet only in the parallel sense. The consolidation of basic tiles of an n-fold pattern such as this into meta-tiles that can tile the plane only non-periodically (not periodically) is discussed in Aperiodic Tilings.

The full 18-gon following the first inflation step is shown in the figure below.

All the tiles meet edge-to-edge and vertex-to-vertex at this stage (with suitable choices in the construction), but notice that this tiling involves some occurrences of two green tiles adjoined to each other "head to toe". At the next inflation and partition stage this will lead to some vertices lying on the edges of other tiles. It's possible to reverse one of the green tiles, but then the inconsistency appears at the neighboring boundary between the yellow and blue tiles. Therefore, at the next stage we necessarily have some vertex-to-edge meetings, as shown in the figure below. We also see the first occurrence of two yellow tiles meeting head to toe, and of a yellow tile with it's apex at the center of a face of a blue cluster.

The red lines mid-way along the sides highlight the borders that do not meet vertex-to-vertex. It's interesting that the region in the lower right corner outlined in red is identical to the original overall slice on the previous stage, although the corresponding region on the left side of this figure is not the same, which implies that the pattern of growth is not cumulative. The tiling needs to begin differently in order to cover larger and larger areas. This raises the interesting question of whether there exists a set of tiles that can tile the plane only asymptotically, in the sense that any given sequence of decisions covers only a finite region, but there is no limit to the size of the finite regions that can be covered. This is conceivable, because for a tiling based on inflation and partition, it's possible that on each stage the pattern in the original core region changes (as in the above example). The beginnings don't "converge" on any stable arrangement for any sequence of arrangements of arbitrarily increasing size.

Return to MathPages Main Menu