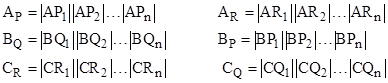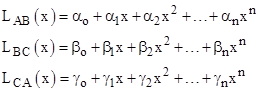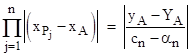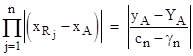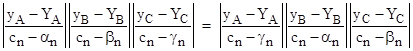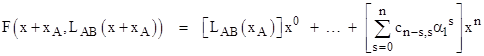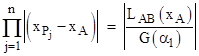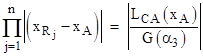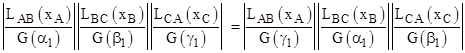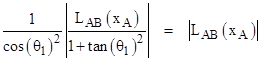Carnot, Organizer of Transversals

Lazare Carnot (1753-1823) was France's leading military planner during the French Revolution, and was heralded as the "Organizer of Victory". (This appraisal was pronounced in his defense when he came near to being indicted for complicity in the Terror.) He instituted universal conscription and was instrumental in creating the French army that was subsequently used by Napoleon Bonaparte to conquer much of Europe. He also contributed directly to Bonaparte's rise by appointing him to lead the Italian campaign. However, in 1797, as a result of a coup d'etat, Carnot was forced to flee France, going first to Switzerland and then to Germany. He returned to France in 1799 and served briefly as Minister of War in 1800.

In addition to being an engineer, military planner, and statesman, Carnot was also a mathematician. Prior to his exile in 1797 he held the chair of geometry in the prestigious Institute of Science. (Upon his expulsion from the Institute the chair was voted to Bonaparte, who also has a theorem named after him.) When not engaged in military or political planning, Carnot devoted his time to writing about geometry and the foundations of calculus.  One of his most famous works was "Reflections on the Metaphysics of the Infinitesimal Calculus". Interestingly, Napoleon often denigrated his political opponents by referring to them as "metaphysicians", saying for example that "We have a dozen or fifteen metaphysicians who ought to be thrown into a pond". He also dismissed the mathematician Laplace for "bringing the theory of infintesimals to administration". Despite his disdain for the administrative abilities of a metaphysicians, Napoleon in 1814 enlisted the support of Carnot, who took over the defense of Antwerp and succeeded in holding it until the peace treaty was signed. After the Battle of Waterloo, Napoleon is reported to have said "Monsieur Carnot, I have known you too late".

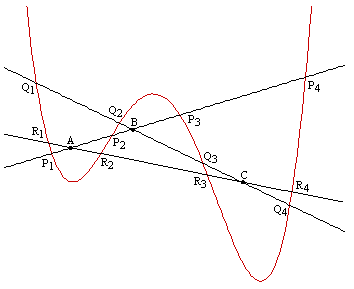
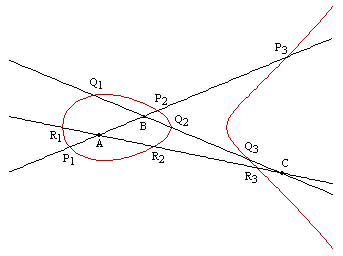
In the area of geometry, Carnot is best known for his theory of transversals. This included a generalization of the ancient theorem of Menelaus which asserts that if a straight line intersects the (extended) edges AB, BC, CA of a triangle at the points P, Q, R respectively, then |AP| |BQ| |CR| = |AR| |BP| |CQ|. Carnot's generalization pertains to a curve of order n intersecting the line AB at the points P₁, P₂, ..., P_n, and the line BC at the points Q₁, Q₂, ..., Q_n, and the line CA at the points R₁, R₂,... , R_n , as shown in the figure below for n = 4.

Given such an arrangement, Carnot defines the quantities

and then asserts a relation analogous to Menelaus' original theorem, namely,

Focusing on polynomials of degree n, a fairly simple algebraic proof for this proposition can be given, and, as is often the case with generalizations, it greatly clarifies the "reason" that the original theorem is true. Let the curve of degree n be represented by the polynomial

and the let three "lines" AB, BC, CA also be represented by polynomials of degree n

Of course, since these are straight lines in Carnot's theorem, the coefficients of terms above the first degree can be taken as zero, but it's convenient to evaluate the more general case, and then specialize to the case of straight lines at the end.

We can shift the x coordinates so that the point A is at x = 0 by replacing each "x" in these equations with x + x_A. Then we note that the n roots of the polynomial

equal the amounts by which the x coordinates of the intersection points P₁, P₂, ..., P_n differ from x_A (the x coordinate of point A). Therefore, letting y_A = f(x_A) and Y_A = L_AB(x_A), the product of these differences is

If we repeat this derivation, replacing the "line" AB with the other line through point A, namely, the line CA, we find that the product of the amounts by which the x coordinates of the intersection points R₁, R₂, ..., R_n differ from x_A is

Notice that if n is greater than 1, and if the loci represented by L_AB(x), L_BC(x), and L_CA(x) are of degree less than n (so that α_n = β_n = γ_n = 0), then the product of the x-distances of the points P_j from the point A is equal to the product of the x-distances of the points R_j from the point A. Analogous relations hold for the x-distances of the point Q_j and P_j from point B, and for the x-distances of the points R_j and Q_j from the point C.

On the other hand, if n = 1 (as in Menelaus' Theorem) and/or if the degrees of the three "lines" equal n, then the values of α_n, β_n, and γ_n are non-zero, so we do not have equality between the two products of x-distances relative to a single vertex of the triangle A,B,C. In this case, we must be content just with equality of the cyclic products, i.e.,

This is more general than Carnot's Theorem, because the three loci AB, BC, and CA are allowed to be of any degree up to n (i.e., they are not restricted to straight lines), but it applies only to the x-distances between points, whereas Carnot's Theorem applies to the "arc lengths" along the loci between points. If the three loci are straight lines, we immediately recover Carnot's Theorem, because we need only multiply each x-distance along a given line by the reciprocal of the cosine of the angle which that line makes with the x axis to give the length of the corresponding segment. Since each line appears in exactly one product on each side of the above equality, we have equal powers of these cosecants on each side, and therefore equality is preserved.

The preceding discussion focused on three loci (lines) intersecting with a single-valued curve, i.e., a polynomial y = f(x). Carnot's theorem actually applies to three lines intersecting with any curve of order n, i.e., any curve defined by F(x,y) = 0 where F is a function of the form

for constants c_j,k where j + k ≤ n. For example, the figure below shows the curve of order three given by F(x,y) = (x−1)(x−3)(x−4) − y².

As before, let P_i, Q_i, R_i for i = 1 to n denote the n intersections of this curve with the lines

respectively, and let point A denote the intersection of lines L_AB with L_CA, etc. We can then construct the polynomial F(x,L_AB(x)) whose roots are the x values of the points P_i. Replacing x with x + x_A in this expression gives another polynomial of degree n in x whose roots are the (signed) x-distances of the points P_i from the point A. Collecting terms by powers of x, this polynomial has the form

Consequently the product of the x-distances of the points P_i from the point A is

where G(α₁) denotes the coefficient (as a function of α₁) of xⁿ in the preceding polynomial. Similarly the product of the x-distances from the points Ri to the point A is given by

and analogous relations hold for the x-distances of the point Q_j and P_j from point B, and for the x-distances of the points R_j and Q_j from the point C. Combining all these relations into two cyclic products, we have

Again noting that we need only multiply each x-distance along a given line by the reciprocal of the cosine of the angle which that line makes with the x axis to give the length of the corresponding segment, and that each line appears in exactly one product on each side of the above equality, we have equal powers of these cosecants on each side, and therefore equality is preserved. This proves Carnot's theorem for general curves of order n.

Notice that α₁, β₁, γ₁ are simply the tangents of the angles that the respective lines make with the x axis. In the special case when F(x,y) is a circle, i.e., F(x,y) = x² + y² − 1, we have G(α₁) = 1 + tan(θ₁)², where θ₁ is the angle of the line AB. In this case, since n = 2, there are two segment lengths in each product, so we need to multiply each term by the square of the cosine of the angle of the respective line. Hence the first factor on the left side of the above equation contributes a total factor of

and likewise for all the other factors. This confirms the fact (as discussed in another note) that the product of the two distances from any point to a circle is constant along all lines through the given point.

It's worth noting that the above theorems need not be limited to just three crossing lines. They can be immediately extended to cover an arbitrary number N of (non-parallel) lines. In general there are N(N−1)/2 points of intersection, and each line has a unique point of intersection with each other line (excluding triple intersections). Clearly for any complete cycle of these lines the above theorems apply. For any such cycle, each vertex occurs on two lines, and each line connects two vertices. In essence, Carnot's general theorem asserts the equality of two products of factors, with each factor associated with a vertex and a line, and the numerators are just functions of the vertex while the denominators are just functions of the line. So, for any given cycle of lines and vertices [L₁, v₁, L₂, v₂, ..., L_N, v_N], one side of the equality consists of products based on the pairings (L₁,v₁)(L₂,v₂)... around the loop, and the other side consists of products based on the pairings in the opposite direction around the loop, i.e., (L₂,v₁)(L₁,v_N)... Obviously these two products are equal, since they are just re-arrangements of the same factors.

Incidentally, one of Lazare Carnot's sons was the physicist Sadi Carnot (named after the Persian poet Sadi of Shiraz), remembered today as one of the founders of thermodynamics (e.g., "the Carnot cycle"). Sadi evidently became interested in the subject after he and his father discussed the (then) emerging technology of steam engines. Another of Lazare's sons was Hippolyte, who served as the French minister of education. One of Hippolyte's sons (also named Sadi) was the President of France from 1887 until his assassination in 1894.

Return to MathPages Main Menu