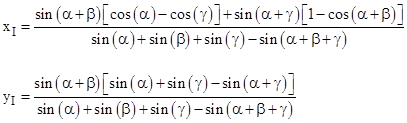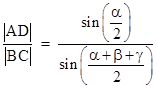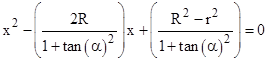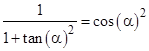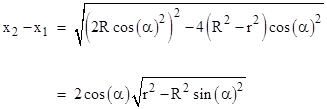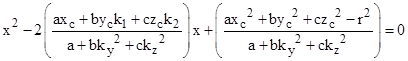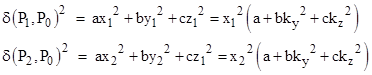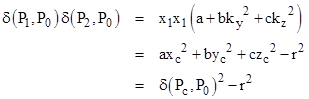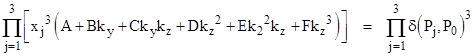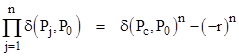Quadrilateral In a Circle

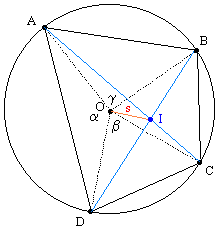
Consider a quadrilateral ABCD inscribed in a circle as shown below.

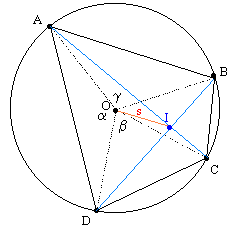
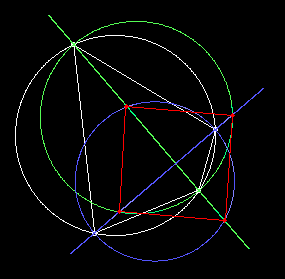
The point O is the center of the circle, and we let α, β, γ denote the angles AOD, DOC, and AOB respectively. The two diagonals of the quadrilateral meet at the point I. The distance from O to I is denoted by s. In terms of Cartesian coordinates x,y with origin at the center, the coordinates of the intersection point I satisfy

We can rotate the figure the figure to place the point A on the positive x axis, and solve these two equations for the coordinates of the intersection point to give

The distance from the center to the intersection point is then given by

We also have the ratio of opposite edge lengths

The diagonals are perpindicular if and only if γ + β = π. An example of this circumstance is illustrated below.

With perpendicular diagonals, we have γ = π – β, so the above expressions reduce to

Of course, the area of the quadrilateral is sin(α) + sin(β). Also in the case of perpindicular diagonals, suppose we take these two diagonals as the diameters of two new circles. Each of these circles intersects the other diagonal in two points. These four points of intersection form a perfect square, with area 2sin(α)sin(β), as illustrated below.

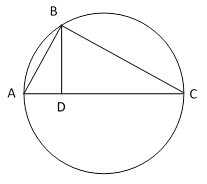
This is a fairly immediate corrollary of Pythagoras's theorem. If AC is the hypotenuse of a right triangle ABC, then the point B is on the circle whose diameter is AC, as shown below. (This can be proven simply by completing the rectangle.)

The conventional statement of "right angle relations" is the one given by Pythagoras and Euclid, which is

However, another necessary and sufficient condition for right angles is

which is the hyperbolic expression of Pythagoras's theorem. This signifies that the height of a right triangle is the geometric mean of the two segments formed by dropping a perpendicular from the apex to the base. We will prove below that the product of the segments of any chord through a given point is invariant, so the right triangles drawn on the two diagonals of the original quadrilateral have the same heights, resulting in a perfect square.

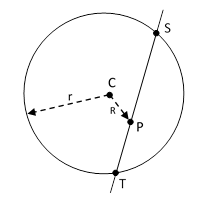
Of course (2) is really just a special case of a more general relation. (See Propositions 35 and 36 of Book III of Euclid's Elements.) Suppose we have a circle of radius r and an arbitrary point on the plane (inside or outside the circle) called P. Draw any line through the point P, and let S,T denote the points of intersection with the circle, as shown below.

Then we have

where R is the distance from P to the center of the circle. Obviously if TS is a diameter of the circle then r² – R² is just the squared height of the perpindicular at P, and equation (3) reduces to (2). However, the nice thing about the more general form (3) is that it works for any line through the circle, not just diameters. Also, note that for any line through the point P the product of the two segments is the same (because the distance from P to the center of the circle is unchanged).

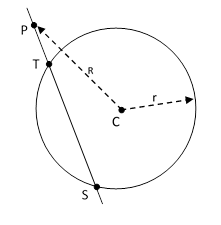
The same theorem applies even when the point P is outside the circle, as shown below.

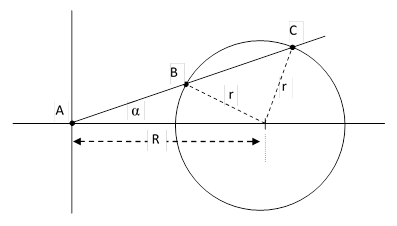
where again R is the distance from P to the center of the circle. In fact, this even works when the line through P does not intersect the circle. In that case the points of intersection have complex coordinates in the plane, and the distances |PT| and |PS| are complex, but they are conjugates, and their product is still the real number R² – r². To prove this algebraically, place a circle of radius r on the x axis of Cartesian coordinates, with its center a distance R from the origin A, and draw an arbitrary line through the origin intersecting the circle at points B and C as shown below.

The equation of the circle is

and the equation of the line AC is

Substituting into the previous expression and collecting terms on x gives the quadratic

Making use of the fact that

the quadratic in x is

which shows that the x coordinates of the two points of intersection B and C satisfy

Since x₁ = |AB| cos(α) and x₂ = |AC| cos(α), it follows from the above relation that

(Euclid’s proof of this proposition based on the Pythagorean theorem – along with a simpler proof based on calculus - are presented in Generalizing Pythagoras and Carnot.) Incidentally, the difference between the roots of the quadratic is

so we have

More generally, given any quadratic curve or surface centered at point P_c = (x_c,y_c,z_c) consisting of the locus of points that satyisfy the equation

where a, b, c, r are constants, we can define the "distance function" δ(P₁,P₂) for any two points P₁ and P₂ by

Now, for any given line through the origin there are constants k_y and k_z such that

so we can find the points of intersection of the line with the conic locus by substituting into the locus equation and collecting terms to give the quadratic in x

The product of the two roots x₁ and x₂ equals the last term. We also have the “distances” from the origin P₀ to the two points of intersection P₁ and P₂

Therefore, we have

Thus the general form of Pythagoras's theorem can be expressed as

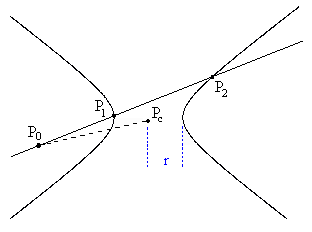
where the sign of δ(u,v) is based on a consistent definition of polarity on the line from u to v. Thus the signs of δ(u,v) and δ(v,u) are opposite. Consequently, if the locus is a circle and the point P₀ is outside the circle, then δ(P₁,P₀) and δ(P₀,P₂) have opposite signs, so the right hand term can be brought over to the left as a positive magnitude. The figure below illustrates the application of equation (4) to a hyperbolic locus.

Moreover, if P₁ = P₂ then the line from P₀ is tangent to the locus and equation (4) reduces to the familiar “Pythagorean” form

The same proposition can be generalized to any homogeneous algebraic function of n variables. For example, consider the function

Using this function we can define the “distance” between two points P₁ and P₂ by the equation

Now consider the locus of points that are a “distance” r from a given central point P_c, i.e., the points satisfying the equation

and also consider an arbitrary line through the origin P₀, with the equations

Substituting these expressions for y and z into the previous equation gives a cubic in x. The coefficient of x³ in this cubic is easily seen to be

and the constant coefficient is

Therefore, letting x₁, x₂, x₃ denote the roots of the cubic in x, we know their product equals (-1)ⁿ times the constant coefficient divided by the coefficient of x³, so we have

The cube of the left hand side can be expressed as

so we have

For the fully general case of an nth degree homogeneous polynomial function f of m variables, we can let P₁, P₂, …, P_n denote the n points of intersection of an arbitrary line through any given point P₀ with the locus δ(P,P_c) = rⁿ, then we have the identity

Return to MathPages Main Menu