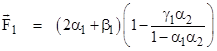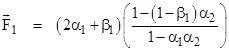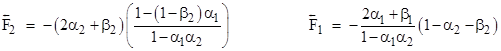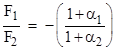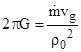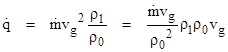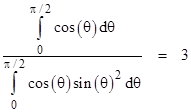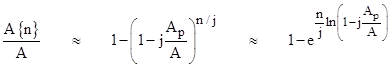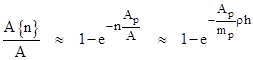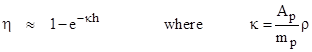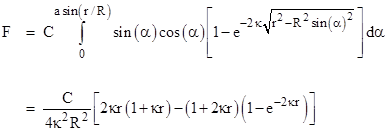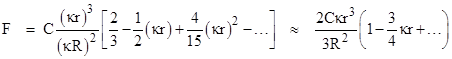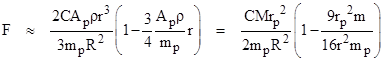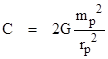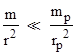Omni-Directional Flux

In his elaboration of Fatio’s model of gravity based on an omni-directional flux of particles, Lesage argued that macroscopic bodies consist of a lattice structure (cages) with slender connecting rods supplying the forces of both tension and compression necessary to maintain structural form and rigidity. Lesage did not explain the forces by which the bars were supposed to maintain their shape, and indeed it’s easy to see that no purely kinetic theory of impulse interactions (from the classical perspective) can possibly account for the coherence and stability of extensive configurations of matter. In view of this, it’s clear that Lesage’s theory was fundamentally misguided, because even if it could satisfactorily account for the observed effects of gravity (which it can’t for other reasons, as explained in Lesage’s Shadows), it would still just amount to replacing one unexplained elementary force of attraction (gravity) with several others, including the absorption force exerted by elementary mass particles on ultra-mundane particles. It is only this absorption that yields the net attractive impulse between macroscopic bodies in the Fatio-Lesage model.

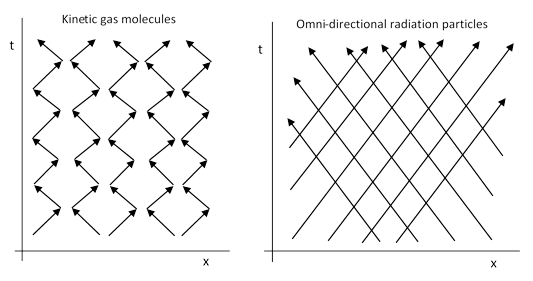
Despite the fact that the underlying premise of the Fatio-Lesage model is inherently self-defeating (not to mention the fact that the model is irreconcilable with the observed facts of gravitation), it’s interesting to evaluate some of the detailed attributes of the model. The most interesting - as well as the most dubious - aspect of the model is the omni-directional radiation field of ultra-mundane particles. This is somewhat cavalierly conceived as consisting of small particles moving in all directions through every point in space and time. First, we must be careful not to confuse this with the microscopic description of a gas or fluid, which can also be described loosely as consisting of tiny particles moving in all directions. The kinetic model of gases is fundamentally different from the Fatio-Lesage concept of an omni-directional radiation field. In one-dimensional space the difference is illustrated below.

The molecules of a kinetic gas are always in motion, but they bounce off each other, and the mean free path length (between collisions) is very small, so for a stationary gas any reasonably sized aggregate of particles has net zero momentum, and each individual molecule remains in a roughly bounded region. In contrast, the particles comprising an omni-directional radiation field do not interact with each other. In fact, for a one-dimensional space we must assume they pass freely through each other. (In higher dimensions we can arrange for many paths to “miss” each other, provided the particles have sufficiently small cross-sections - but this is more problematic than one might think, as discussed below.)

It might seem that these two situations are essentially the same (at least for point-like particles in one dimension), because if we imagine two identical omni-directional particles approaching each other and then passing through each other, we could just as well say they bounced off each other, by exchanging their identities. In principle, as long as all collisions are perfectly elastic, and as long as nothing else interferes, the two models can indeed be regarded as equivalent. However, if we introduce other entities that interact with these particles - possibly even absorbing these particles, and moving at some non-zero speed relative to the isotropic frame of these particles - the two situations are very different. First, suppose we introduce two perfectly elastic and opaque barriers into each of the one-dimensional spaces illustrated above, and assume that in both cases the omni-directional radiation particles are also perfectly elastic. In both cases the particles trapped between the barriers will simply bounce off the walls and remain trapped, so the aggregate forces on both sides of the barriers are equal. Now suppose the barriers absorb a certain fraction of the particles that strike them. In both cases the number of particles between the barriers will gradually be depleted, whereas the external bombardments will continue unabated, so there will arise a net force tending to drive the barriers together. Either of these models could be (and both have been) suggested as the basis for mechanistic models of gravitation, the first being a fluid “sink” model, and the second being a Fatio-Lesage radiation model.

It can be shown that two fluid sinks in a fully-developed incompressible potential flow field are subjected to a force of attraction proportional to the inverse square of the distance between them. This force arises from the variations in static pressure due to the bulk velocity of the fluid as it flows into the two sinks. A similar force of attraction occurs between two sources in an incompressible fluid, because, just as in the case of sinks, the flow field has its maximum velocity (and hence minimum static pressure) in the region directly between the singularities. On the other hand, a source and a sink exert an inverse-square force of repulsion on each other. Since an inverse-square attraction exists between two sinks, and also between two sources, it’s possible to imagine particles pulsating in a fluid, acting alternately as sinks and sources. If their pulsations are in phase with each other they will be subject to a more or less continuous inverse-square force of attraction, whereas if they have opposite phases they would be subject to an inverse-square force of repulsion. This effect can actually be demonstrated by using ultra-sonic waves to induce synchronized pulsations of bubbles rising in a liquid. The bubbles are drawn together by their mutual force of attraction.

However, the fluid sink (and/or source) mechanism has major failings as a putative explanation for gravity. First, the concept of an incompressible fluid entails the acceptance of instantaneous action at a distance, which is not really mechanistic at all. Even if we postulate a compressible fluid, variations in the static pressure (which putatively produce the gravitational force) will be correlated with the macroscopic bulk velocity of the flow, not the microscopic velocities of the individual molecules. It is the same mechanism as the one that produces lift on a wing. Assuming the bulk mass-flow rate into the sink is on the order of the velocity of the planets around the sun, the drag force on the planets would be comparable to the gravitational force, contrary to observation. On the other hand, if we suppose that the bulk velocity of the fluid flowing into each sink is extremely great, we are led to an unacceptably high rate of mass accretion for gravitating objects, leading again to unacceptable drag. (Furthermore, such a highly dynamic flowfield could not become fully developed for each changing configuration of material bodies.) Needless to say, the fluid sink model cannot escape the drag and mass accretion problems by imagining that the fluid circulates in a vortex motion, for all the reasons Newton described in Principia (such as the existence of non-equatorial orbits). As for the unacceptable mass accretion, we might argue (as Riemann suggested) that the fluid entering a material body flows into other dimensions. However, accounting for gross violations of conservation laws by postulating unseen dimensions is usually regarded as highly ad hoc. Some have sought to avoid the mass accretion problem by positing that massive particles alternate between sinks and sources with the correct phase relations, but then we need to explain how the phase synchronization is maintained, especially since the action of the fluid tends to oppose the perfect in-phase (or perfect out-of-phase) condition and drive towards an equilibrium phase relation with null force. Some external agent is necessary to induce and maintain the required phase relation, so even if this approach worked (which it doesn’t, due to the problems noted above) we would only have succeeded in “explaining” one simple force (gravity) in terms of a different and very convoluted and occult force.

Since the fluid sink mechanism does not provide a satisfactory model of gravity, the concept of an omni-directional radiation field was proposed, first by Newton’s friend Nicholas Fatio, and then later by Georges-Louis Lesage. One crude way of evoking the basic premise is to imagine that at every point in space there are winds blowing in all directions at once. Now, if these were actual “winds” in a real fluid this situation would be impossible, because the winds would simply collide with each other and come to a stop. But according to the Fatio-Lesage conception, the “ultra-mundane” particles comprising the omni-directional radiation field do not interact with each other, because their cross-sections are so small in comparison with the mean distance between neighboring particles that they almost never collide. Most of them cross the entire universe without striking anything.

The discrete flux constituted in this manner, with each of its constituents moving at equal and very high speed, crosses the universe; consequently, it has come from places beyond the world, and that is why these are termed ultramundane corpuscles.

(It’s interesting that Lesage’s term for his gravific particles is “ultra-mundane”, which literally means other-worldly or super-natural.) The ultra-mundane “winds” comprised of these tiny particles just pass through each other without any appreciable interference. The force of gravity is then supposed to result from the shadow effect, i.e., massive bodies intercept a certain fraction of the radiation particles, so two neighboring bodies effectively shield each other (slightly) from the radiation in their respective directions, resulting in a net force of attraction on each body.

Before examining the consequences of an omni-directional flux in three-dimensional space, it’s worthwhile to consider the one-dimensional case. The figure below shows the interactions between two general quasi-static objects (at rest with respect to the isotropic frame of the radiation) and the radiation flux coming from one direction. The fractions (assumed to be the same in both directions) of the incident radiation that each object reflects, absorbs, and transmits are α_j, β_j, and γ_j respectively.

The reflections impart twice the momentum as the absorptions, and the transmissions impart none at all (because we assume the transmitted particles are not slowed), so the normalized net force on the left hand object due to absorption is

and due to reflection is

for a total net force (due to the rightward flux) defined as positive in the positive x direction of

Since α_j + β_j + γ_j = 1, we can eliminate γ_j from this expression to give

Similarly the total force which the rightward flux imparts to the object on the right is

By symmetry the forces exerted on the two objects by the leftward flux are

Therefore, the combined total forces exerted on the two objects by the two-directional flux are

This shows that if there is no absorption (i.e., if β₁ = β₂ = 0) then there are no net forces exerted on the objects. If there is some absorption but no reflection at all, then the objects are subjected to equal and opposite forces of magnitude β₁β₂. If both reflection and absorption are present, but the ratio of reflection to absorption is the same for both objects (as would be the case for a Fatio-Lesage model because of the low density of the elementary opaque particles of matter), we can define a parameter μ such that μ = α₁/β₁ = α₂/β₂, and the forces on the two objects can then be written as

These are not exactly equal in magnitude, so this model of gravity does not (in general) exactly satisfy Newton’s third law, according to which the sum of these two forces must vanish, i.e., the ratio of the forces must equal −1. Here we actually have the ratio

which equals −1 only if the reflectivities are both zero (or exactly equal, which could be the case only for equal masses). Of course, the magnitude of the mutual forces would be nearly equal provided the fraction of incident radiation reflected from the two objects is sufficiently small. In this approximation, we have

where μ is the ratio of reflectivity to absorbtivity, which can be made arbitrarily large. Consequently, if we accept imperfect conservation of momentum, we can use reflectivity as a multiplier to increase the force of gravity for a given absorption. Incidentally, this is contrary to the conclusion of Poincare, who wrote

We shall be led to results no less fantastic if, in opposition to Darwin’s views, we endow Lesage’s corpuscles with an elasticity that is imperfect but not nil. It is true that the vis viva of the corpuscles will then not be entirely converted into heat, but the attraction produced will equally be less, so that it will only be that portion of the vis viva converted into heat that will contribute towards the production of attraction, and so we shall get the same result. A judicious use of the theorem of virial will enable us to realize this.

Poincare overlooked the fact that reflection can amplify a small anisotropy in the flux produced by a small amount of absorption. Darwin excluded this condition because (as noted above) a mixture of absorption and reflection necessarily violates Newton’s third law for the mutual gravitational force between two bodies. If we accept some degree of non-conservation of momentum, then reflection can contribute significantly to the net force, and the virial theorem does not contradict this, because that theorem applies only to situations in which momentum is strictly conserved, which need not be the case. However, empirical observation places a limit on the degree to which momentum conservation may be violated. The reflectivities α₁ and α₂ are proportional to the masses of the two bodies, so for unequal pairs (such as the Sun and the Earth) even a very slight cumulative change in momentum would be apparent over millions of years.

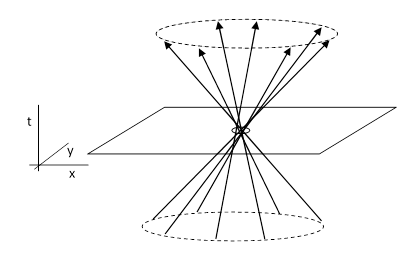
The preceding describes some effects of an omni-directional flux in just one dimension, in which there are just two discrete directions. In two or more spatial dimensions there are infinitely many directions, and in three or more spatial dimensions there is no uniform pattern of rays that is symmetrical in all possible directions. (This corresponds to the fact that we can easily divide a circle into a regular n-gon for any integer n, but there are only five regular polyhedrons.) The usual way of conceiving of an approximately uniform distribution of discrete rays over all space in all directions is to imagine that in each volume of size V we can randomly select n points from a uniform distribution over this volume, and then to each of those points we assign a particle with speed u in a direction of motion that is randomly chosen from a uniform distribution over the sphere of directions. (To avoid the analog of Olber’s paradox for gravity in an infinite eternal universe with uniformly distributed material bodies it’s necessary to assume the particles are re-randomized on some scale.) The approximately conical family of world-lines of the radiation particles passing through one small region of space can be visualized as shown below.

Now, if the mean free path lengths of the particles was actually infinite, then in order for the local uniformity to persist over time it would be necessary for the distribution of particle positions and velocities to be uniformly distributed over the union of this volume with all the neighboring volumes, and so on. Ultimately, to postulate an eternally uniform distribution in an infinite space, we need the velocities and positions at the present instant to be uniformly distributed over the entire space – which is not possible, because there is no such thing as a uniform probability distribution over infinite space, just as there is no such thing as a uniform distribution over the real numbers. Lesage himself seems to have been as least dimly aware of the paradoxical aspects of his posited omni-directional radiation field when he wrote

A uniform distribution of the corpuscles is necessary for weight and attraction to act equally in all directions. As far as a body at rest is concerned, it can be shown that it is enough to have 3,141,592 different directions in the ultramundane corpuscles for a massive body not to alter its weight by one part in 500,000. The many questions to which this distribution gives rise are more curious than useful, so we do not think it necessary to consider them.

Admittedly a similar foundational problem arises when we attempt to postulate a perfectly relativistic infinite spacetime containing matter, because the rest frame of the center of mass cannot have been truly randomly selected from a uniform distribution over the full range of possibilities. However, in the case of Lesage’s radiation field (with infinite mean free path lengths), the problem is much more acute, because each and every one of the infinitely many ultra-mundane particles must be drawn independently from the putative (but impossible!) uniform distribution over infinite space. Fortunately, most physicists are not mathematicians, and are not overly vexed by such foundational concerns, and in any case we can assume some finite mean free path, or a finite universe, or some other feature to mitigate this problem.

Another unique feature of an omni-directional flux of impenetrable particles is that, unlike a kinetic gas, it has no continuous limit. The behavior of a gas approaches that of a continuous medium, at each point of which the substance has a definite state of motion (and pressure, temperature, etc). In contrast, an omni-directional flux of impenetrable particles cannot be carried over to a continuous limit, because at each point it must be moving in all directions at once. The limit of such a flux is actually a fractal: between every two particles moving in one direction there is a particle moving in the opposite direction, and between every two particles moving in opposite directions there is a particle moving perpendicularly to them. Of course, at each point there is a definite mean velocity, just as there is in a gas, but the crucial difference is that the velocity of each molecule of a gas also has a mean velocity over short time intervals, and this approaches the mean velocity of the gas at that point. For an omni-directional flux the mean velocity of each particle at a given point over time does not approach the mean velocity of the flux at that point.

Setting aside any concerns about the intelligibility of an omni-directional radiation flux, Lesage posited that macroscopic bodies consist of small elementary particles (which he took to be polyhedral skeletons, but which can just as well be taken to be tiny spheres), whose individual shapes and relations to one another are maintained by unexplained elementary attractive forces. We also posit an unexplained force mechanism enabling these particles to absorb and retain some of the ultra-mundane particles that strike them.

One of the interesting consequences of this model is the amount of energy transferred from the ultra-mundane flux to ordinary massive bodies. To minimize drag effects, it is necessary to assume the ultra-mundane particles move at enormous speeds. In fact, Lesage argued that they must move at “a hundred thousand times the speed of light”, and subsequent authors have established even greater lower bounds on the speed. This enormous speed implies that the radiation field has an incredibly high effective “temperature”, so it should be expected to impart tremendous amounts of heat into ordinary bodies. Of course, the transfer of heat depends on the extent to which the radiation flux interacts with ordinary matter, which can be inferred from the observed properties of gravity.

To assess the amount of heat, consider two parallel infinite flat slabs of ordinary matter, with mass densities ρ₁ and ρ₂ kilograms per square meter. A well-known property of Newtonian gravity is that the force of attraction of a particle of mass m to an infinite flat wall with mass per unit area of ρ is 2πGρm, independent of the particle’s distance from the wall. Therefore, the force of attraction per unit area for our two infinite flat slabs is

From our preceding analysis of the one-dimensional case with two barriers, and setting the reflectivities to zero (we will discuss later the consequences of non-zero reflectivity), we know that the force of attraction due to the flux normal to the walls is

where dm/dt is the flux mass flow rate per unit area (normal to the walls) and vg is the speed of the flux particles. The dimensionless absorption coefficients β₁ and β₂ for ordinary (sparse) bodies are proportional to the mass densities of the respective walls, so there is a reference density ρ₀ such that β₁ = ρ₁/ρ₀ and β₂ = ρ₂/ρ₀. Making these substitutions and equating the gravitational force with the net flux force, we have

This is based on the net force, which is actually the difference between the momentum of the absorbed flux in the leftward and rightward directions. The total absorbed flux is the sum of these two fluxes. The equations for the leftward and rightward components derived previously can be summed to give

The corresponding energy flux (per unit area for slab 1) is v_g/2 times this momentum flux, so we have

Substituting from the gravitational equation for the fractional quantity, and dividing through by ρ₁ (which is the mass of slab 1 per unit area), we get the energy flux per unit mass for one dimension

This was based on the premise that the direction of the flux is normal to the slab, but in fact the flux incident on any small region arrives uniformly from all directions. Of each ray of flux, only the absorbed component of that ray normal to the slab contributes to the net force, whereas the entire absorbed flux contributes to energy transfer. Therefore, the energy flux is proportional to the integral of unity (squared) over the hemisphere of directions above any given point on the slab, and the momentum flux is proportional to the integral of sin(θ)² over the same hemisphere of directions. Thus to achieve a given net absorbed momentum flux in the normal direction, the absorbed energy flux given by the preceding equation must be increased by the factor

As a result, the absorbed energy flux per unit mass in three spatial dimensions is

Now, recall that the reciprocal of the parameter ρ₀ is the cross-sectional area of a unit mass, i.e., the projected opaque area of a unit mass of ordinary matter. Lesage’s theory requires this area to be essentially independent of the shape or orientation of the material. An upper limit on this area, corresponding to a lower limit on ρ₀, can be inferred from the absence of any diminution in the operation of gravity near large massive objects. For example, if the Earth absorbed an appreciable fraction of the flux passing through it, then two test object would attract each other less strongly near the Earth than they do far out in space. No such shielding or saturation effects are observed. From the absence of such effects we can say the Earth’s opaque area is no more than 10⁻⁶ of it’s macroscopic cross-section, and therefore the opaque area of one kilogram is no more than (2.1)10⁻¹⁷ square meters. Thus we have ρ₀ ≥ (4.7)10¹⁶ kg/m².   Inserting this value along with the gravitational constant into the preceding equation, and setting v_g equal to “just” the speed of light, we find that the rate of energy absorption of each kilogram of matter is (1.8)10¹⁶ Joules per second. Consequently the Earth is absorbing (1.1)10⁴¹ Joules per second. In comparison, the total energy output of the Sun is (4)10²⁶ J/sec, so the Fatio-Lesage theory requires us to believe the Earth is absorbing heat at a rate (2.6)10¹⁴ times greater the Sun’s total power output. Needless to say, this would vaporize the Earth in a fraction of a second. Even worse, if we accept Lesage’s argument that v_g must be at least 10⁵ times the speed of light, then the Earth must absorb (2.6)10¹⁸ times the Sun’s output. Laplace subsequently carried out an analysis of aberration, showing that v_g in the Fatio-Lesage theory must be 10⁶ times the speed of light, so this increases the energy absorption by another factor of ten. Based on more modern observational limits, Poincare determined that v_g could not be less than 10¹⁷ times the speed of light, which implies that the Earth’s rate of energy absorption must be (2.6)10³⁰ times the Sun’s output power. These lower bounds are substantially greater than those derived in the note on Lesage’s Shadows, the reason being that the bounds derived in that note (like those derived by Poincare) are based on the energy flow corresponding to just the net momentum flux, whereas here we have taken into account the entire momentum flux.

The preceding was based on the assumption of zero reflectivity, which is necessary for strict conservation of momentum, but if we allow for some small violation of Newton’s third law (within empirical limits) it is possible to multiply the absorptive force of gravity by a multiplier (1+2μ) where μ is the ratio of reflection to absorption. From the absence of any noticeable violations of Newton’s third law we can infer that μβ can be no greater than a certain limit L₁, and in order to provide the observed force of gravity we know that β times the square root of 2μ is not less than another limit L₂, so it follows that μ is no greater than 2(L₁/L₂)². This permits us to achieve the observed force of gravity with an amount of absorption that is reduced by about a factor of 10⁻¹⁰, so the energy per unit mass is reduced by the same factor. This still implies that the Earth absorbs energy at a rate ranging from 10⁴ Suns (if v_g is “just” the speed of light) to 10²⁰ Suns (if v_g is 10¹⁷ times the speed of light).

As discussed previously, to determine the resultant force of the shadowing effect for two massive bodies of arbitrary shape and size, it is sufficient to note that each elementary opaque particle of matter is compelled toward each other such particle by a force inversely proportional to the square of the distance between them (since this is how the angular region subtended by an object varies with distance), and the effects are additive because we assume the particles are so sparsely arranged that they present almost no overlap in their projected areas in any direction. (Of course, this leaves unexplained what forces maintain the shapes of massive bodies, both on the macroscopic and the microscopic scale, and what forces are responsible for the absorption of ultra-mundane flux, and so on.) However, the angular resolution required to impart exactly the same gravitational force to each elementary particle in a large body is extreme, and it may seem more plausible that macroscopic bodies take advantage of averaging. This greatly reduces the angular resolution requirements for inverse-square accuracy on the scale of the solar system, but it also implies heating and entropy production of massive bodies – adding to the already ruinous heating problem of all Fatio-Lesage models.

Another reason for examining the force on massive bodies from a macroscopic standpoint is to assess the effects of saturation and shielding when the density of matter particles becomes great.  A massive macroscopic body of density ρ in an omni-directional radiation field, consider a slender shaft of length h and cross-sectional area A residing entirely within the massive body. The number n of elementary opaque particles inside this cylindrical region is

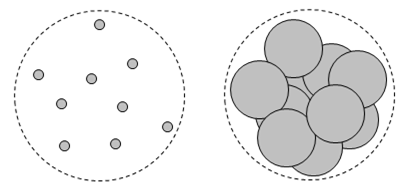
The cross-sectional area of each particle is A_p = πr_p², and the particles are assumed to be randomly and uniformly distributed throughout the macroscopic body. For a sufficiently small number of sufficiently small particles, the particles in the cylinder have a total area projected along the cylinder’s axis equal to the sum of their individual areas, because the individual areas are so small that it is highly improbable there will be any overlap between them, as illustrated in the two figures below.

To assess the effects of overlap, let us partition the set of n particles into sets consisting of j randomly selected particles, where the integer j is chosen to be as large as possible with no significant overlap between the particles. (We will find that the precise value of j is unimportant.) We assert that the normalized areas of sets of j randomly placed particles can be treated as the probabilities of independent events. This is the reason we grouped the particles into sets of scattered particles, so that the position of each small portion of each set is independently located, and hence the areas of unions and intersections closely match the probabilities of statistically independent events.

Letting A_j denote the projected area of each set of j randomly-placed particles (so A_j  ≈  jA_p), the projected area A{n} of the union of n/j such sets is given by

Making use of the approximation  ln(1−x)  ≈  −x  for small x (which we can assure by choosing jA_p small enough), and substituting the previous expression for n, this becomes

showing that the result is fairly insensitive to the choice of j. Thus the fraction of the ultra-mundane flux (in a given direction) that is intercepted as it traverses a distance h through a region with mean mass density ρ is

This can also be written in the form

where ρ_p is the density of an elementary mass particle. If the exponent is small compared with 1, then we have η = κh approximately, i.e., the fraction of intercepted flux is directly proportional to the path length. On the other hand, as the number of particles in the cylinder increases, there will be more and more overlap of their projected areas, until saturation is reached, and essentially all the projected cross-sectional area of the cylinder is covered by one or more particles.

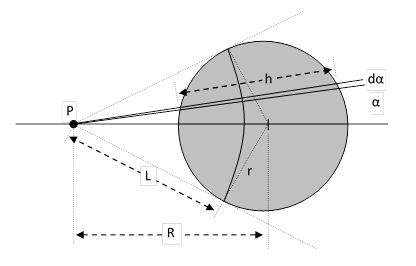
The vector sum of the intercepted flux on all the rays through a given point is proportional to the net force on a test particle at that point. The value of this force for a point P near a spherical macroscopic object can be inferred from the figure below.

The fraction of the ultra-mundane flux intercepted by the particles of the massive body along the incremental angular ray dα at an angle α from the axis is 1 – e^-κh where

This applies to all the rays at an angle α from the axis, the union of which is a conical shell with the vertex at P. Each perpendicular slice of this shell is a ring of radius Lsin(α) where L is the distance of each point on the ring to the point P. Thus the circumference of the ring is 2πL sin(α), and since the width of the ring is Ldα, the spherical area of the ring is 2π L² sin(α)dα. As a fraction of the total spherical area of radius L, this is simply sin(α)dα. The momentum perpendicular to the axis of this cone cancels out, so the net force consists of just the components parallel to the axis, which gives a factor of cos(α). Combining these results, the net force on an elementary particle located at P is

where C (with units of force) is the total integrated absolute value of the radiation pressure over an isolated elementary particle of matter. If κr is much smaller than 1, it’s convenient to expand this in powers of κr to give

Taking the first two terms of the series and substituting from the definition of κ, this can be written as

This is the force on a single particle of matter, so to find the force on a small object of mass m we multiply this by m/m_p, which gives

The two factors in parentheses on the right represent the gravitational constant G, and since we know this really is constant for a wide range of values of m/r², the first-order correction must be negligibly small. With this assumption, the total compressive force C on an elementary massive particle is

which is (loosely speaking) twice the force of gravity between two elementary particles at a distance of one particle radii, which makes sense, because the force on each of two adjacent opaque particles ought to be roughly half the total compressive force on an isolated particle. Thus we arrive at the same result we would get by simply considering the elementary opaque particles, demonstrating that the macroscopic approach does not add any insight in the sparse-matter regime.

This “universal pressure” in Lesage’s theory must have been intriguing to Poincare, because he inferred the existence of just such a pressure in his 1905 paper on Lorentz’s electron theory, as a means of maintaining the cohesion of an electron consistent with Lorentz covariance. However, as far as I know, Poincare never commented on this connection. If we knew the mass and radius of Lesage’s elementary particles of matter, we could infer the compressive force C necessary to give the observed gravitational constant G. Unfortunately modern knowledge of elementary particles and quantum physics does not support the idea that all gravitating entities (nor all entities subject to gravity) are composed of elementary particles with a well-defined ratio of mass to radius. For example, photons have no rest mass at all, and an indeterminate “radius”. Also, electrons are believed to be point-like particles, at least to the accuracy that sizes can be determined. Of course, it could be argued that the real fundamental particles are on the order of the Planck scale, which is far below our ability to measure.

It’s worth noting that in the above discussion we glossed over a questionable point, namely, the requirement that, in order for the gravitational constant to be really constant for a wide range of values of m/r², we must have

In other words, the gravitational acceleration at the surface of the macroscopic body must be much less than the gravitational acceleration at the surface of the microscopic particles of which the macroscopic body is composed. Without some compensating model of the inter-molecular forces, this inequality violates a basic requirement of coherence, because it implies that, at the boundary between two adjacent massive bodies, the constituent parts of the bodies are more strongly attracted to each other than the overall bodies themselves.

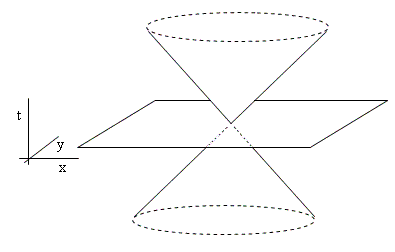
Incidentally, it's possible (with perhaps an excess of imagination) to discern a loose analogy between the Fatio-Lesage model of gravity and the spacetime model of general relativity. The key ingredient of Fatio's model is the omni-directional flux of ultra-mundane particles, converging on and diverging from each point in space with a fixed characteristic speed. Compare the illustration of this flux given above with the illustration of the null cones of Minkowski spacetime shown below.

Obviously the ultra-mundane cones are formally similar to the null cones of relativistic spacetime, especially if the speed of the ultra-mundane particles is identified with the speed of light. (Lesage was not consistent about this; he sometimes asserted that the ultramundane corpuscles move at the speed of light, whereas at other times he suggested that they move many times faster than light.) The world-lines of the ultra-mundane particles correspond to the null rays of Minkowski spacetime. In effect, the Cartesian rejection of instantaneous action at a distance was vindicated – albeit in a non-mechanistic way – by the relativistic field theories of Maxwell and Einstein, according to which the “forces” of both electromagnetism and gravitation propagate on null cones characterized by a fixed speed.

In the Fatio-Lesage model the presence of a nearby mass could be seen as reducing the speed of the flux from the direction of that mass, so the ultra-mundane cone is no longer symmetrical, but instead is “tilted” inward toward the gravitating mass. Likewise in general relativity the presence of a nearby mass has the effect of making the light cone non-symmetrical, tilting them toward the mass. In both models, the result is a tendency for a test particle at this point to veer toward the nearby mass. Fatio conceived of this tendency as being due to an imbalance in the force exerted by the flux, but this can be identified with the effect on geodesic paths of spacetime curvature associated with variations in the null cone structure. Of course, the behavior of an omni-direction flux does not reproduce the behavior of the ten metric potentials in general relativity. (For example, the Fatio-Lesage model produces unacceptable aberration of gravity if the corpuscles are assumed to move at the speed of light.) Nevertheless, it is an interesting analogy.

Return to MathPages Main Menu