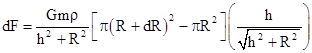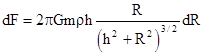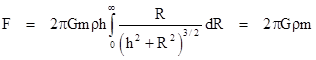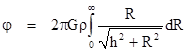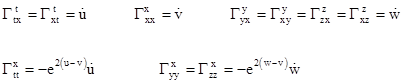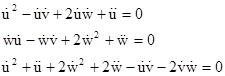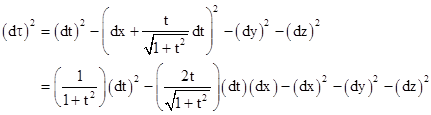An Infinite Wall

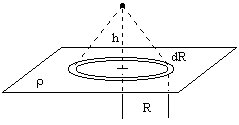
What is the gravitational field of an infinite flat plane? Let ρ denote the mass density of this infinite wall per unit area, and consider a test particle of mass m located at a distance h from the wall, as shown below.

In Newtonian terms, the incremental force dF on this particle contributed by an annular ring of radius R and incremental width dR is just the projection onto the perpendicular of the total forces exerted by each element of the wall around the circumference of the annular region. Thus we have

Expanding this expression in the first order differential, we get

Integrating from R = 0 to ∞, we find that the total force experienced by the particle is

Thus the force exerted on the particle is independent of the distance h from the wall. In other words, there is a constant uniform acceleration field extending to infinity on both sides of the wall.

It's interesting to compare this result with the force exerted on a test particle near a spherical surface in the limit as the sphere's radius increases to infinity. Intuitively we might be tempted to think the result should be the same, whether we consider the test particle to be inside or outside the sphere. However, the force on a particle inside a spherical surface is always zero, whereas the force on a particle outside a spherical surface is equal to the force that would be exerted by the same total mass concentrated at the center of the sphere. (See Newton's Proposition LXXI.) On this basis, for any finite distance from the surface, the force on an external particle would approach 4pGρm, exactly twice the force exerted by an infinite flat wall.

Although the Newtonian analysis yields a seemingly well-behaved finite force, it's worth noting that the gravitational potential given by

is infinite everywhere. This infinite potential suggests that there will be difficulties when we attempt to evaluate the same physical situation in the context of general relativity. To see why, consider again the case of a spherical shell of mass in the limit as the shell's radius increases to infinity. According to Birkhoff's theorem, the field due to a spherically symmetrical configuration of mass is unique (up to a constant). As in the Newtonian case, the only contribution to the field at a given point is due to the mass at a lesser radial distance from the center of the configuration, and this mass produces a field with the Schwarzschild metric. Therefore, we can consider the field near the surface of a spherical shell of radius R and fixed mass density ρ in the limit as the radius goes to infinity. Again, the "attraction" toward the shell for test particles in the interior is zero, independent of the radius. For the region outside the shell we see that the Schwarzschild radius 2m increases in proportion to the square of the radius, so it lies progressively further and further outside the shell as the shell's radius increases. This implies that for any fixed mass density the entire universe is inside the Schwarzschild radius of an infinite flat wall.

We cannot apply the usual Schwarzschild coordinates in the limit as the radius goes to infinity because then, proportionately speaking, a test particle at any fixed distance from the wall will be at a location arbitrarily close to the singularity. We can, however, evaluate the situation with respect to momentarily co-moving coordinates. This gives well-behaved results for any non-zero distance from the wall. We find that the intrinsic curvature of the radial distance-vs-time manifold is K = –2m/r³, and since m is proportional to r² this implies that the curvature vanishes in the limit as r increases. This is consistent with the Newtonian result that an infinite wall produces a perfectly uniform and constant acceleration field. Such a field, in the context of relativity, has no intrinsic curvature, as shown by the fact that it can be completely transformed away over a non-zero region of spacetime by adopting a suitable system of coordinates.

The local proper acceleration for a test particle initially at rest at a radial distance r in a Schwarzschild field is –m/r², and since m is proportional to r² for our spherical shell we see that the local proper acceleration approaches a constant at a distance r+h from the center of the configuration in the limit as r increases, for any fixed h. Again this corresponds to the Newtonian case, and from this correspondence we infer that half of this acceleration applies for a perfectly flat plane.

There is, however, some reason to question the validity of this interpretation. We referred to the acceleration of "a test particle initially at rest", but in the interior region of a Schwarzschild spacetime (i.e., inside the radius 2m) the worldline of a particle is always advancing toward the center, just as in the exterior region a particle is always advancing toward the future. In view of this, it isn't clear that we can arbitrarily specify trajectories of particles in a universe with an infinite flat wall. On the other hand, we can question whether the Schwarzschild topology of a spherical shell carries over to the case of an infinite flat plane distribution of matter. The factor of 1/2 between the limiting spherical shell and the infinite flat plane shows that not all the properties of the limiting shell carry over to the plane.

To resolve these questions, we must solve the Einstein field equations explicitly for the field of an infinite flat plane, and see if the properties of this solution compare with the Newtonian results. In terms of a static coordinate system x,y,z,t, where x is the space coordinate perpendicular to the wall and y,z are the space coordinates on planes parallel to the wall, as shown below.

We can restrict the range of possible metrics based on symmetry considerations. We seek a stationary coordinate system, so the metric coefficients must be independent of t. In addition, the field is clearly independent of the transverse coordinates y and z, so we consider a diagonal metric of the form

where g_yy(x) = g_zz(x). Since the metric coefficients are strictly functions of x, we can use dots to signify total derivatives with respect to x. Also, we will find it convenient to define the functions u(x), v(x), and w(x) such that

In these terms we can write the non-zero Christoffel symbols for this metric as

The only components of the Ricci tensor that are not identically zero in these circumstances are the diagonal components R_tt, R_xx, and R_yy (= R_zz). Setting these components to zero leads to the following conditions

Before solving this in general, consider the special case where the g_xx, g_yy, and g_zz metric coefficients are constants, and only the temporal coefficient g_tt varies with x. In that case we have dv/dx = dw/dx = 0, so the above equations reduce to simply

which has the solution du/dx = 1/(x+α) and therefore u = ln(x+α) + ln(β) where α,β are arbitrary constants. From this we get

Actually if we express u in terms of g_tt and substitute into the preceding equation we get the condition

and differentiating again gives

Thus the metric coefficient can be anything of the form

for constants A, B, and C. Assuming A is non-zero we can shift and re-scale the x coordinate so that g_tt(x) = x², and so our line element is

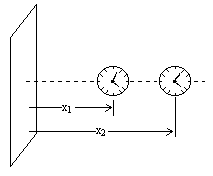
To interpret this physically, consider two stationary clocks located at the "distances" x₁ and x₂ from the wall, as shown below.

Since the clocks are not moving, we have dx = dy = dz = 0 along their respective worldlines, and therefore

Consequently we have dτ₂/dτ₁ = x₂/x₁. This is qualitatively consistent with our expectation that a clock will run more slowly the nearer it is to the wall, but the quantitative relation is not correct, because in a uniform acceleration field we expect the ratio of frequencies to be the same for any fixed difference between the distances to the wall. In other words, we expect dτ/dt to vary not in proportion to the distance from the wall, but in proportion to the exponential of the distance to the wall. Furthermore, if we evaluate the geodesic equations of motion (returning now to the more general case where v and w need not be constants) we find that the geodesic equation for the "acceleration" in the x direction is

and thus for a momentarily stationary particle we have

The line element for a stationary particle gives (dt/dτ)² = e^–2u, so we can make this substitution to give

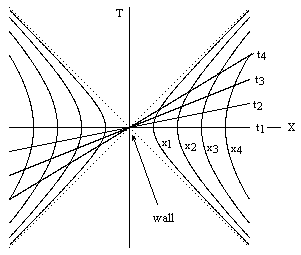
For the metric given above we have e^-2v = -1 and du/dx = 1/(x+α), so the acceleration is simply -1/(x+α). In other words, the acceleration of a test particle released from "rest" is inversely proportional to (an arbitrary constant plus) the distance from the wall. This is not surprising, because the metric (1) is nothing but the usual Minkowski metric of flat spacetime in the coordinates T,X,Y,Z transformed by making the substitutions T=(x)sinh(t), X=(x)cosh(t), Y=y, Z=z, so each line of constant x is subjected to constant proper acceleration relative to the Minkowski X,T coordinates, as shown in the figure below, but this acceleration is 1/x, so it does not correspond to a uniform gravitational field.

In order to have the same acceleration at every distance from the wall, we need to set d²x/dτ² equal to a constant k in the preceding equation, which implies

Consequently we have

which shows that we cannot achieve a uniform acceleration field with constant v. Allowing v to be variable, but still holding constant w, the conditions necessary for the Ricci tensor to vanish reduce to

Substituting from the geodesic condition for constant acceleration, this becomes

which has the solution du/dx = 1/(2x) so from the prior equation we have dv/dx = –1/(2x). We can integrate these to give u = (1/2)ln(x), v = (–1/2)ln(x) + πi/2 and therefore

Taking g_yy = g_zz = –1, the line element has the form

This satisfies the vacuum field equations and gives a fixed acceleration from rest independent of distance from the wall. However, it still does not give a constant frequency ratio for light traveling a fixed distance in the x direction. Instead, the ratio of clock rates is proportional to the square root of the ratio of x values. We could, of course, transform to a different coordinate perpendicular to the wall, defined such that the frequency ratio of clocks at a fixed distance from each other is constant. If we define X such that x = e^X then we have dx = e^XdX. Making these substitutions, we have

Naturally these changes of coordinates do not alter the vanishing of the Ricci tensor. We get a formally similar result (with e^X replaced by e^2X) if we substitute into the previous metric line element (1), so these are essentially the same solution, expressed in terms of different coordinate systems. Specifically, the x coordinate in (2) is proportional to the square of the x coordinate in (1). Unfortunately when we use a coordinate system in terms of which the local acceleration from rest is independent of distance to the wall, we do not have a constant frequency ratio for space intervals of a given size, and vice versa.

Finally we consider the fully general case, where g_tt, g_xx, and g_yy (= g_zz) are all non-constant functions of x. In this case the first two conditions for the vanishing of the Ricci tensor, together with the geodesic condition for constant acceleration from rest, give

Thus we have

Also, substituting for dv/dx in the third condition for the vanishing of the Ricci tensor we get

so this condition reduces to

Substituting for the quantity on the left into the previous expression for 2(dw/dx) and re-arranging gives

Equating this to the previous expression for du/dx, we arrive at the condition

From this it follows that

Thus we can take

Recalling that the metric coefficients are g_tt = e^2u, g_xx = e^2v, and g_yy = g_zz = e^2w, this gives the line element

This metric satisfies the vacuum field equations and gives the same proper acceleration from rest for all positions, but again it fails to give a fixed frequency ratio for a given change in x. If we define X such that x^4/3 = e^X then we have dx = (3/4)e^3X/4dX. Making these substitutions, we have

This gives a fixed frequency ratio, but not fixed proper acceleration from rest.

The fundamental difficulty in constructing a truly uniform gravitational field over an extended region can be seen by considering several equally spaced rockets along the x axis in Minkowski spacetime, each undergoing the same constant proper acceleration. The spacing between the rockets remains constant with respect to the original rest frame, but with respect to each rocket's co-moving inertial rest frames the spacing increases continuously. In contrast, the spacing between several stationary elevator cars positioned in a vertical line in a gravitational field does not increase.

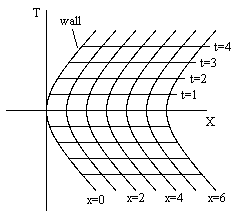
Another approach is to simply begin with flat Minkowski spacetime with the standard coordinates T,X,Y,Z and transform to a system of coordinates t,x,y,z such that each stationary worldline is undergoing the same constant proper acceleration. The T,X and t,x planes are illustrated below.

The wall is located along the worldline identified as "x = 0". We can take t = T (and y = Y and z = Z) and then define the x coordinate as

From this we have

Substituting into the Minkowski line element, we get

This is quite different from the previous metrics we have been considering, first because it is not stationary, and second because it is not diagonal. Furthermore, the time coordinate t does not represent the local time of the co-moving inertial coordinates at any point (except for t = 0).

Return to MathPages Main Menu