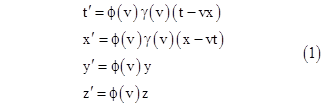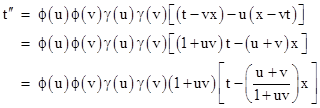|
On Groups and Lorentz’s Scale Factor |
|
|
|
In another note we discussed how in 1904 Lorentz showed that Maxwell’s equations are invariant under transformations of the form |
|
|
|
|
|
where |
|
|
|
|
|
After carrying along the ϕ(v) factor as an undetermined function for most of his paper, Lorentz eventually gave a convoluted and unsatisfactory dynamical argument for setting ϕ(v) = 1. In contrast, Einstein (1905) explained quite simply that if we require the transformation with the parameters +v followed by the transformation with parameter –v yield the original coordinates, we have ϕ(v)ϕ(–v)=1, and then noting that the effect in the perpendicular (y and z) directions must be the same for +v and –v by isotropy, it follows that ϕ(v) = ϕ(–v), so we have ϕ(v)=1 (neglecting reflections). Einstein then observed that these transformations form a group. |
|
|
|
In 1905 Poincare reviewed Lorentz’s 1904 paper, correcting a couple of algebra mistakes, but otherwise agreeing with everything that Lorentz had said – with the exception of the derivation of the scale factor. Poincare had written in a letter to Lorentz that Lorentz’s derivation was inadequate. In Poincare’s 1905 paper he simply argued that (what he called) the Lorentz transformations form a group (in the mathematical sense) only if ϕ(v)=1. |
|
|
|
The whole of all these transformations, joined with the whole of all rotations of space, must form a group; but, so that it is thus, it is necessary that ϕ(v)= 1; one is thus led to suppose ϕ(v) = 1, a consequence which Lorentz had obtained in another way… That holds, as I said, because ϕ(v) = 1 is the only assumption for which the Lorentz transformations form a group. |
|
|
|
Lorentz evidently accepted this, since in a review of Poincare’s papers on this subject Lorentz echoed the claim: |
|
|
|
I already spoke about the necessity for posing ϕ(v) = 1 (constancy of the equatorial radius of the electron). I will not repeat here the demonstration given by Poincaré and I will only say that he showed the mathematical origin of this condition. One can consider all the transformations which are represented by formulas (1), with different values for speed -v, and the corresponding values of γ(v) and ϕ(v), this last coefficient has to be regarded as a function of v; we can add to it other similar transformations which we deduce from (1) by changing the directions of the axes, and finally by arbitrary rotations. The postulate of relativity requires that all these transformations form a group and that is only possible if ϕ(v) has the constant value 1. |
|
|
|
It’s worth noting that Lorentz and Poincare still thought of the transformations in terms of the shape of the electron, with the condition ϕ(v)=1 corresponding to the hypothesis of “constancy of the equatorial radius of the electron”. This makes it less surprising that they would even consider the possibility of expansion or contraction in the direction transverse to the direction of motion. Neutral dust particles, separated by arbitrarily great distance and moving in parallel in the x direction, would not be expected to be drawn closer together or pushed further apart in the y and z directions simply due to being accelerated in the x direction, but one can imagine that an electron’s size and/or shape changes in a variety of ways when set in motion. Indeed there were competing theories, e.g., Langevin, in which the electron contracted in the direction of motion but expanded in the transverse directions to maintain constant volume. Poincare rightly noted that (tacitly assuming the same transverse expansion for v and –v), Langevin’s theory was inconsistent with the transformations (1) forming a group. Poincare and Lorentz go even further, and assert that those transformations can form a group only if ϕ(v) equals 1. |
|
|
|
But is this really true? Admittedly the usual rotation transformations are unitary, so it would seem strange to combine them with non-unitary boosts, but is it really true that non-unitary boosts cannot form a group? Einstein’s observation was that the transformations (1) with ϕ(v)=1 form a group, which is obviously true, but Poincare (echoed by Lorentz) is claiming the converse, i.e., he claims (in his 1905 paper) that if the transformations form a group then ϕ(v)=1. This is actually not true for boosts of the general form (1). Recall that a set of transformations form a group just if it has a unique identity transformation, every transformation has a unique inverse, and the set is closed under associative composition of any two elements. Now, the transformations of the form (1) have the identity element with v=0 provided γ(0)=1 and ϕ(0)=1. Also, each transformation has a unique inverse. It only remains to ensure that the composition of any two transformations of the form (1) with real parameters u and v is also a transformation of the form (1) with real parameter w. |
|
|
|
If we apply a transformation with parameter v to a system of coordinates t,x,y,z to yield t′,x′,y′,z′, and then apply a transformation with parameter u to the latter coordinates to yield the new coordinates t″,x″,y″,z″, the composition gives |
|
|
|
|
|
|
|
Taking w = (u+v)/(1+uv), this reduces to |
|
|
|
|
|
|
|
This will be a transformation of the form (1) with the real parameter w just if |
|
|
|
|
|
|
|
In view of the identity |
|
|
|
|
|
for any constant k, where atanh is the inverse hyperbolic tangent, the condition (2) is satisfied if we define |
|
|
|
|
|
|
|
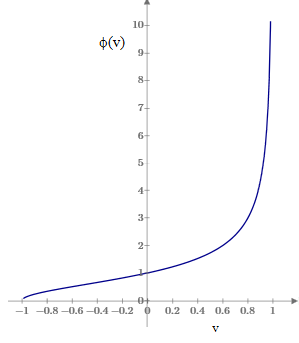
for any constant k. With k=0 this gives the usual degenerate function ϕ(v) = 1, but if we choose, say, k=1, we get the function shown below. |
|
|
|
|
|
|
|
This same function also yields group compositions for the x, y, and z coordinates, so transformations of the form (1) constitute a group if ϕ(v) is defined by this function. It satisfies the conditions ϕ(0)=1 and ϕ(v)ϕ(–v)=1. Hence the group property alone does not imply that ϕ(v) equals 1. We need some argument invoking symmetry (isotropy), such as Einstein’s requirement that the transformation of the coordinates perpendicular to the axis of motion must be independent of the direction of motion along that axis. In a paper published in 1906 Poincare omitted the explicit claim that the group property requires ϕ(v)=1, but simply noted that by taking ϕ(v)=1 the quantity t2–x2–y2–z2 is invariant. More generally, we have |
|
|
|
|
|
|
|
where v is the speed of the primed coordinate origin in terms of the unprimed coordinates. One might think that this singles out one particular state of motion along the x axis as the v=0 frame, but in fact the relativistic composition of velocities ensures that the relations between any frame and all the others – in terms of velocities expressed in that frame – take this same form. Our arbitrary choice of sign for the inverse hyperbolic tangent determined the direction of increasing and decreasing ϕ. |
|
|
|
The physical significance of this more general Lorentz transformation is subtle in some respects. For example, the velocity composition formula w = (u+v)/(1+uv) is independent of ϕ, so that is unaffected, regardless of what value(s) we assign to ϕ. Also, by construction, Maxwell’s equations are invariant under this general transformation, so electromagnetic phenomena would satisfy the same physical equations in terms of any of these systems of coordinates, at least up to scale factors. But scale factors are physically meaningful. For example, if we adopt non-unit values of ϕ, the spatial coordinates perpendicular to the direction of motion are expanded or contracted, but the we know empirically that identically constructed measuring rods would have equal spatial extents in those directions. This can be traced back to the hypothesis that the electron (as conceived by Lorentz and Poincare) doesn’t deform in the transverse directions, but it can also be seen in the fact that accelerating a row of neutral free particles in parallel, perpendicular to their axis, would not result in them being forced apart or drawn closer together. Thus for operationally based coordinates, we must have ϕ = 1. But this is for reasons of physical symmetry. It is not sufficient to stipulate that the transformations form a group, as explained above. |
|
|
|
One might argue that the ϕ(v) factor in (1) is unobservable or physically meaningless, since, in any given frame, the same scale factor is applied to all the space and time coordinates, so it might be regarded as nothing more than a trivial “gauge” freedom to change the individual units of spatial and temporal measure, while maintaining all the same dimensionless ratios. From this point of view, setting ϕ(v)=1 is conventional to maintain consistent units. |
|
|
|
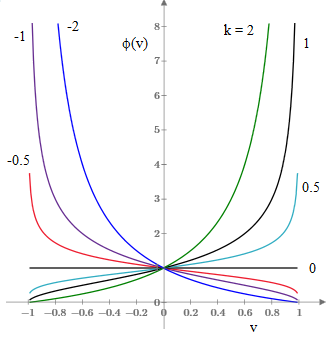
Incidentally, the previous plot showed the ϕ function for k = 1, but we could define ϕ(v) by equation (3) for any fixed value of k, each of which makes the transformations (1) into a group satisfying (2). The figure below shows the ϕ function for a range of value of k. |
|
|
|
|
|
|
|
As noted above, the normal isotropic Lorentz transformation is given by setting k=0 which yields ϕ(v)=1. |
|
|