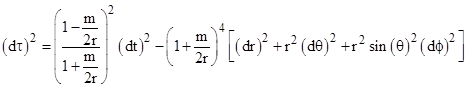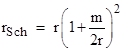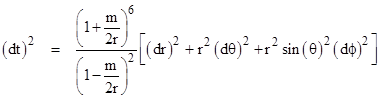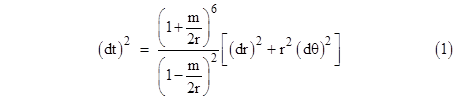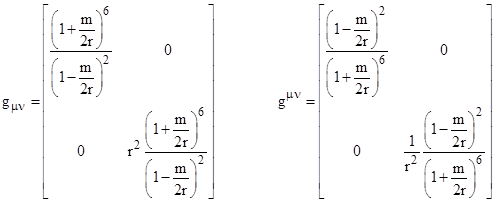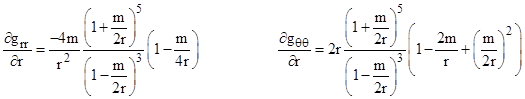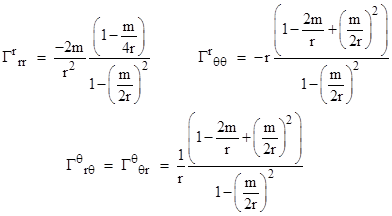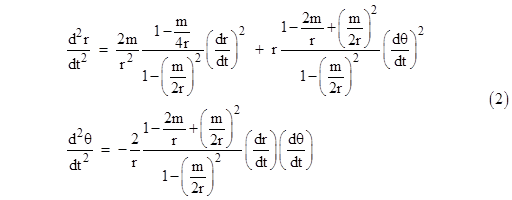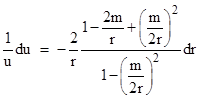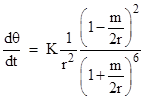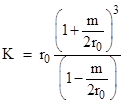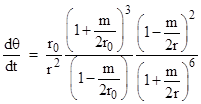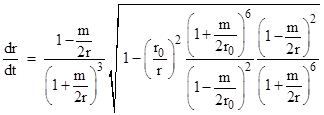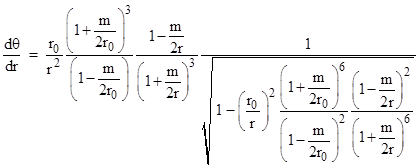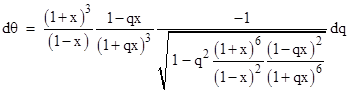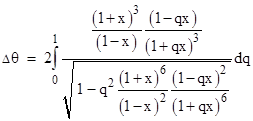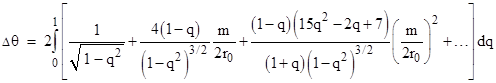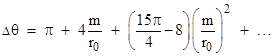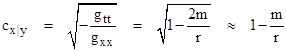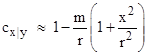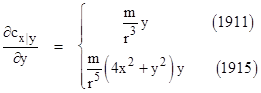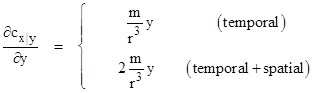Light Deflection in Isotropic Coordinates

The article on Bending Light presents a derivation of the relativistic prediction for light deflection in the gravitational field of a spherical body. That derivation is given in terms of Schwarzschild coordinates, and applies to the angle between the asymptotes of a ray of light approaching from and receding to infinite distance. It’s worth noting that locally measured angles are not properly represented in Schwarzschild coordinates, because the speed of light is not isotropic in terms of those coordinates. Only the central angles are valid in terms of those coordinates. The derivation of the light deflection angle in terms of Schwarzschild coordinates was valid only because we determined the angle between the central asymptotes, which is essentially representative of the angles viewed from Earth of a ray grazing the limb of the Sun, because the Earth is sufficiently distant from the Sun in comparison with the perhelion distance of the grazing rays. However, as discussed in the note on Celestial Deflections, if we wished to determine the angles for rays whose closest approach to the Sun is comparable to the Earth’s orbital radius, it would not be valid to simply integrate the Schwarzschild coordinate expressions to those distances. In order to compute the angles in more general circumstances (not merely the asymptotes), we need to use isotropic coordinates, which are defined such that the coordinate speed of light at every location is the same in all directions.

As discussed in the note Refractions on Relativity, the Schwarzschild solution to Einstein’s field equations for a non-rotating spherically symmetrical body in terms of isotropic coordinates is

where the t, θ, and ϕ coordinates are the same as the corresponding Schwarzschild coordinates, but the “r” coordinate is related to the Schwarzschild radial coordinate r_Sch by

It’s worth noting that, although the perimeter of a circular orbit of radius r_Sch is 2π(r_Sch), the perimeter of a circular orbit of radius r (the isotropic radial parameter) is not 2πr. Now, since light follows null trajectories (dτ = 0), we have the positive-definite metric for light paths

Restricting our attention to a single plane through the center of mass by setting ϕ = 0, the paths of light reside on a manifold with the metric

This can be regarded as the (positive-definite) line element of a two-dimensional surface (r,θ), with the parameter t serving as the metrical distance. The null paths satisfying the complete spacetime metric with dτ = 0 are stationary if and only if they are stationary with respect to (1). This implies Fermat’s Principle of “least time”, i.e., light follows paths that minimize the integrated time of flight, or, more generally, paths for which the elapsed Schwarzschild coordinate time is stationary. Therefore, we need only determine the geodesic paths on this surface. The covariant and contravariant metric tensors are

and the only non-zero partial derivatives of the components of g_μν are

so the non-zero Christoffel symbols are

Taking the coordinate time t as the path parameter (since it plays the role of the metrical distance in this geometry), the two equations for geodesic paths on the (r,θ) surface are

These equations of motion describe the paths of light rays in a spherically symmetrical gravitational field in terms of isotropic coordinates.

To quantitatively assess the angular deflection of a ray of light passing near a large gravitating body, note that in terms of the variable u = dθ/dt the second geodesic equation (2) has the form

Integrating both sides, we get

where C is a constant of integration. Taking the exponential of both sides gives

where K is a constant. To determine the value of K, we substitute this expression for dθ/dt into the metric equation (1), divide through by (dt)², and evaluate it at the perihelion r = r₀, where dr/dt = 0. Solving the resulting equation for K, we get

Therefore we have

Now we can substitute this into the metric equation divided by (dt)² and solve for dr/dt to give

Dividing (dθ/dt) by (dr/dt) then gives

Integrating this from r = r₀ to ∞ gives the mass-centered angle swept out by a pulse of light as it moves from the perihelion out to an infinite distance. If we define q = r₀/r we have dr = −(r/q)dq, and if we let x denote m/(2r) the above equation can be written in the form

The swept angle from perihelion to infinite distance is the integral of this from q = 1 to 0, and the total swept angle from incoming to outgoing asymptote is twice this amount. Thus we have

Since x is much less than 1, we can expand the integrand into a series in powers of x as follows:

Evaluating the integral term by term, we get

If the ray was perfectly straight, the swept angle would be π, so the remaining excess terms represent the gravitational deflection. As expected, the first-order deflection is 4m/r₀, which is twice the naive Newtonian deflection as discussed in Bending Light. This first order term agrees exactly with that expressed in terms of Schwarzschild coordinates, but the coefficient of the second order term is different. For the Schwarzschild coordinates the coefficient of this term is 15π/4 – 4, which is approximately 7.781, whereas for the isotropic coordinates it is 15π/4 – 8, which is approximately 3.781. The reason for this difference is that the meanings of the radial coordinates are different. A perihelion radius of r₀ in terms of isotropic coordinates corresponds to a slightly greater radial Schwarzschild coordinate, so the deflection is slightly less when comparing to the deflection expressed in terms of the Schwarzschild radial coordinate. This small correction to the first-order term appears as a shift in the second-order coefficient.

As noted above, the advantage of isotropic coordinates is their conformal property, meaning that all local angles for light rays are correctly represented, whereas for Schwarzschild coordinates only the central angles are uniformly represented. This is why either set of coordinates will work for determining the angles of the asymptotic directions, but for determining intermediate directions along the path (for example, if we want the angle swept out between two arbitrary radial positions) we must use isotropic coordinates.

From a historical perspective, it’s interesting to apply the method used by Einstein in his 1911 and 1915 papers to evaluate the light deflection. Recall that, in both cases, Einstein was implicitly using coordinates such that a circle of radius r centered on the origin has circumference 2πr, which is the basis of the Schwarzschild radial coordinate, although he didn’t yet have the exact Schwarzschild solution, even in 1915. As explained in “Doubling the Deflection”, in 1911 his metric was the Minkowski metric except with g_tt = 1 – 2m/r. Thus the spatial part was still flat, so he had g_xx = −1, and the tangential speed of light along a path that is essentially parall to the x axis at nearly constant y was therefore

On the other hand, by 1915 he had included the spatial curvature required by the final form of the vacuum field equations, so in terms of these coordinates he had (approximately)

and therefore

Using Huygens’ method, the total asymptotic deflection is given by integrating the expressions

with y = r₀ as x ranges from –∞ to +∞. This leads to the results described in “Doubling the Deflection”, showing that the relationship between these functions is not simple, and it just so happens (seemingly) that the integral of 1915 evaluates to twice the integral of 1911. However, if Einstein had been working in terms of isotropic coordinates (using the radial coordinates that makes the speed of light isotropic at each point, rather than the Schwarzschild radial coordinate), the metric to the first order can be written as

On this basis the first-order expressions to be integrated for just the temporal part and for the combined temporal and spatial parts are simply

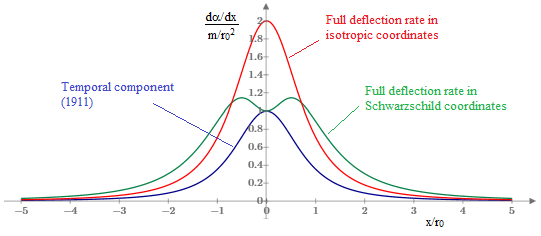
Thus in terms of isotropic coordinates the deflection per unit distance along the path is literally twice as large at every point. These deflections rates are shown in the figure below.

Einstein wrote in his popular 1916 book that “half the deflection is produced by the Newtonian field of attraction of the sun, and the other half by the geometrical modification (“curvature”) of space caused by the sun”. Note that he identified the time-time component as the Newtonian effect. On that basis, the statement is true for the overall asymptotic deflection, regardless of our choice of coordinates, but it is true at each point along the path (to the first order) only in terms of isotropic coordinates.

Return to MathPages Main Menu