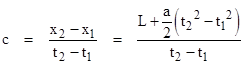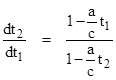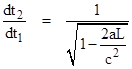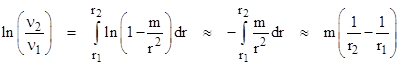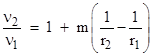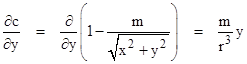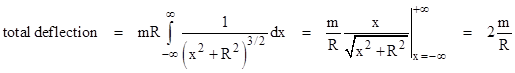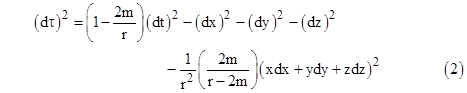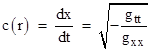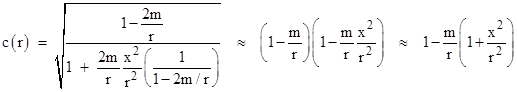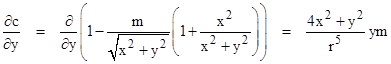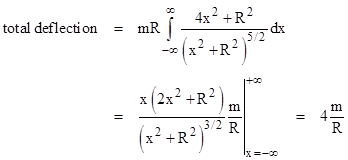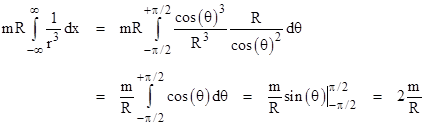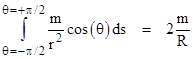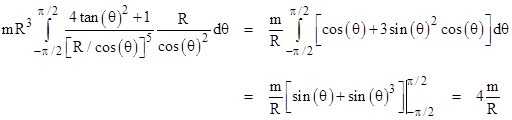Doubling the Deflection

Because of the analogy between the propagation of rays of light and the motion of bodies, I thought it not amiss to add the following Propositions for optical uses; not considering the nature of the rays of light, or inquiring whether they are bodies or not, but only determining the trajectories of bodies, which are extremely similar to the trajectories of rays.

                                                              Isaac Newton, Principia, 1687

In 1911, from simple reasoning based on the equivalence principle, Einstein made two predictions regarding the behavior of light in a gravitational field. First, the frequency of a beam of light should be shifted by a certain amount between the emission and absorption at two different heights (potentials) in a gravitational field. Second, a ray of light should be deflected by a certain amount as it passes by a gravitating body. In 1915 Einstein completed the general theory of relativity, which of course was founded on the equivalence principle, but in a more comprehensive sense. In the completed theory of 1915 the predicted frequency shift for light in a gravitational field is the same as Einstein had predicted in 1911, but the total amount of deflection (between the asymptotic directions) which a ray of light is predicted to undergo due to passing by a gravitating body is twice as much as he had predicted in 1911. We describe below how these two sets of predictions were reached, and why the predicted frequency shift remained the same between the theories of 1911 and 1915 while the angular deflection doubled.

Consider an elevator car of height L accelerating upward at some constant rate a. At any given instant we can choose an inertial coordinate system such that the elevator is instantaneously at rest, and in terms of which the positions of the bottom and top of the car are

If a pulse of light is emitted from the bottom of the elevator at time t₁ and absorbed at the top of the elevator at time t₂, we have from special relativity the relation

where c is the speed of light. Writing this in the form

we can evaluate how much the reception time varies for a given change in the emission time by taking the differentials

Hence we have

Solving equation (1) for t₂ at the time t₁ = 0, and inserting into this equation for that same instant, we get

For a sequence of pulses emitted from the bottom of the elevator and absorbed at the top, the frequencies will be inversely proportional to the incremental time intervals between the pulses, so the emission and absorption frequencies (near the time t₁ = 0) will be proportional to

Thus, light emitted with frequency ν₁ from the bottom of an upwardly accelerating elevator car will arrive at the top of the car with a reduced frequency (i.e., red shifted) by this factor. According to the equivalence principle, the same must hold true in an elevator car that is stationary in a gravitational field with an acceleration of gravity equal to a. Of course, in a real gravitational field the acceleration varies with distance from the gravitating body, so in order to determine the total frequency shift for a large change in position we must take the product of these ratios for many small steps, over each of which the acceleration is gravity is approximately constant. Now, choosing units so that Newton’s gravitational constant and the speed of light are both equal to 1 in terms of free-fall coordinates, the acceleration of gravity at a distance r from the center of a spherical body of mass m is a = m/r², so for each unit of radial distance L=1 we get a factor of 1 – m/r² for the frequency. Since m/r² is typically a very small quantity, the logarithm of the total factor from r₁ to r₂ is given by

Hence, from simple considerations of the equivalence principle, Einstein predicted in 1911 that light of frequency ν₁ emanating from a point at a radial distance r₁ from the center of a spherical gravitating body of mass m would be received at another radial distance r₂ with a frequency ν₂ shifted by the factor

As discussed from a more sophisticated point of view in Section 6.1, this can also be seen as a simple consequence of the different rates of proper time at the two radial distances. For stationary positions in a gravitational field, the only non-zero term on the right side of the line element

is the term involving just the coordinate time differentials, so the “rate” of proper time at any stationary location is

Again from the equivalence principle it’s clear that g_tt is of the form 1 – 2m/r, from which it follows that the rate of proper time is (to the first order) given by 1 – m/r. Notice that this frequency shift depends only on the “time-time” component of the metric tensor. This is because, regardless of the spatial metric, each wave crest of light follows the same spatial path from emission to absorption, so the spatial path doesn’t affect the difference between emission times and reception times.

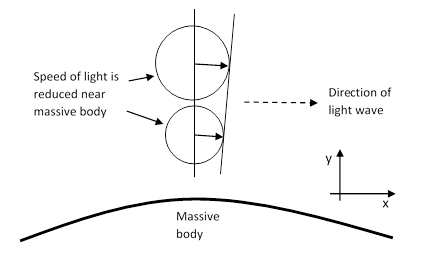
In the same paper of 1911, Einstein noted that the same variation in proper time versus radial distance which implies a frequency shift would also produce deflection in a ray of light passing near a massive body. To be precise, a ray of light passing at a distance R from the center of a body of mass m (again in geometric units) would undergo a deflection of approximately 2m/R radians. This is a direct result of applying Huygens’ principle to a wave front passing through a region in which the speed of the wave varies with position, as depicted in the figure below.

This situation is more complicated than the simple change in frequency between two stationary locations, because it involves the variation not just of proper time but of the speed of light, which depends on the space components as well as the time components of the metric. If we suppose that the metric is essentially Minkowskian, except for the value of g_tt implied by the equivalence principle, we have

A light ray has dτ = 0, so this simplistic metric implies that the speed of light for a ray moving in (predominantly) the x direction is

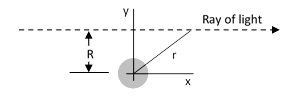
Now, we can read directly off the figure that the direction of the wave front changes by an amount equal to –∂c/∂y per unit of distance along the direction of the wave. Note that the total deflection is extremely small, so to the first order of approximation we can consider just the x component of its motion as depicted below.

The partial of c with respect to y is

To compute the total deflection of the wave front along the entire path, Einstein simply integrated this over the path. Of course, for any deflection at all, no matter how small, the path will eventually move by a significant amount in the y direction, but Einstein’s calculation relies on the fact that nearly all of the deflection occurs within some reasonable proximity of the gravitating body, so for convenience we can simply set y = R and integrate x from negative to positive infinity. Thus we have

(See below for a comment on how Einstein actually performed this integration.) Not surprisingly, this is the same deflection that is predicted based on a naïve application of Newton’s theory. This was to be expected, because Newton’s theory can be expressed in geometrical terms as just the time-time component of general relativity. (See Section 8.5 for more on this.) However, in the full theory of general relativity, completed in 1915, Einstein found that the predicted deflection is actually 4m/R, i.e., twice his earlier prediction (and twice the naïve Newtonian prediction). The reason for this doubling of the deflection is that the full theory takes into account not just the variation of the time-time component of the metric, as in equation (1), but also the variation of the spatial components.

As explained in Section 6.6, the line element for a spherically symmetrical gravitational field in the full theory of general relativity is given not by (1), but rather by

This is just a re-writing of the Schwarzschild metric in quasi-Minkowskian coordinates, and it differs from (1) by the last term involving the space differentials. Since the “time-time” coefficient is the same, the frequency shift is unaffected, but we must account for the spatial curvature in our assessment of the directional deflection of light rays. Einstein announced this in the same paper of November 18, 1915, in which he presented for the first time the calculation of the anomalous precession of Mercury’s orbit (see Sections 6.2 and 8.10). However, he merely summarized the new light deflection prediction in this paper, stating that

This theory… produces an influence of the gravitational field on a light ray somewhat different from that given in my earlier work, because the velocity of light is determined by g_mndx^mdxⁿ = 0. Upon the application of Huygens’ principle, we find… after a simple calculation, that a light ray passing at a distance R suffers an angular deflection of magnitude 4m/R, while the earlier calculation… had produced the value 2m/R... In contrast to this difference, the result concerning the shift of the spectral lines by the gravitational potential… remains unaffected, because this result depends only on g_tt.

In his review article of 1916 he filled in the details of this “simple calculation”, which is essentially just a repetition of the 1911 derivation, except that the variations of the spatial components of the metric are taken into account. In both derivations we have dτ = 0, and we take dy = dz = 0 (to the first approximation) along the path, so the speed of light is

The difference between the 1911 and 1915 derivations is simply that in 1911 Einstein took g_xx = –1, in accord with the quasi-Minkowskian metric (1), so he only considered the part of the deflection arising from the “time-time” component of the metric, whereas in November 1915 he realized that the full metric is actually given by (2), with varying spatial coefficients. In particular, we have

Therefore, the speed of light (along this path) is actually given, to the first order in the small quantities m/r, by the expression

Now, proceeding just as he did in 1911, Einstein determined the total deflection using Huygens’ principle by first evaluating the partial derivative

Then, recalling that y = R, he integrated this along the entire path to give the total deflection

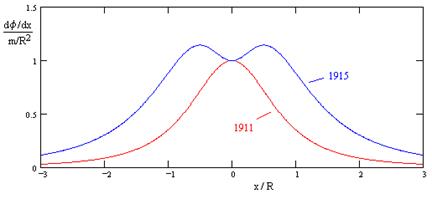
Thus the spatial curvature doubles the amount of deflection from the naïve Newtonian prediction and Einstein’s preliminary 1911 calculation. However, this does not arise from simply doubling the rate of deflection at every point on the path. This can be seen by plotting the rates of deflection as a function of x/R for the theories of 1911 and 1915 as shown below.

According to the calculation of 1911, the rate of deflection is a maximum at the point of closest approach to the gravitating body (i.e., where x = 0 and y = R), and the calculation of 1915 gives the same rate of deflection at that point. However, the 1915 calculation, accounting for the spatial as well as temporal curvature, shows that, in terms of the usual Schwarzschild coordinates, there are two points of maximum rate of deflection for a path of constant y, at the locations x = ±R/2. The integrated area under the 1911 curve is 2, whereas the integrated area under the 1915 curve is 4, but this plot shows that the relationship between the two is not as simple as one might think based on the fact that the latter happens to give twice the total deflection of the former (to the first order in m/r in the small-deflection limit). It should be noted, though, that the relationship between the deflection rates for the time-time metric and the full spacetime metric depends on our choice of coordinate systems. For example, in isotropic coordinates (described in Section 8.4) the full spacetime deflection rate is simply twice the time-time rate at all points of the path.

People sometimes wonder how this doubling of the deflection can be reconciled with the equivalence principle and the “elevator” thought experiment on which Einstein’s 1911 calculation was based. If we imagine a ray of light entering an elevator car horizontally at the middle of one wall, and if we assume the car has a downward acceleration of m/r², then the path of the ray relative to the car (according to the equivalence principle) should be h = (1/2)(m/r²)x² where h is the height of the ray referred to its entry height. For very small deflections we have dh/dx = tan(θ) ≈ θ and hence dθ/dx = m/r² = m/(R² + x²) where R is the minimum distance. This applies when the acceleration is perpendicular to the ray of light, but at other locations the perpendicular component of acceleration of the elevator car must be scaled by the cosine, i.e., by the factor R/(R² + x²)^1/2. Integrating this product over all x, we have the same formula for the total deflection as given in Einstein’s 1911 derivation from Huygens’ principle (see above), yielding the result 2m/R. This is the unambiguous consequence of the equivalence principle in flat space. Since the equivalence principle still applies in the 1915 theory, how do we reconcile this with the fact that the 1915 theory predicts twice this amount of total deflection?

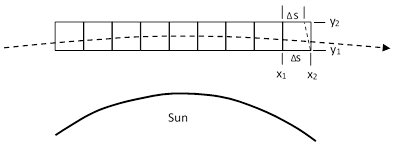
Intuitively, Einstein’s 1911 prediction was only half of the correct value because he did not account for the cumulative effect of spatial curvature over a sequence of small regions of spacetime, within each of which the principle of equivalence applies. This can be understood from the figure below, which depicts a ray of light passing through a sequence of “Einsteinian elevators” near the Sun.

By evaluating the absolute spacelike intervals Δs along the top and bottom of each “elevator car” we find that the walls which are parallel in terms of the local coordinates of the car are not parallel in terms of the global coordinates (except for the central car, where the 1911 and 1915 calculations do predict the same rate of deflection). In general, the simple argument based on the equivalence principle gives the correct rate of deflection in terms of the local coordinates, i.e., it gives the difference between the angles that the ray of light makes with the opposite walls of a car, which are parallel in terms of the car’s local coordinates, but this doesn’t account for the fact that the walls are not parallel in terms of the global coordinates. As we’ve seen, when integrated over the entire path of a light ray, the total deflection from the standpoint of a global system of coordinates is twice the deflection that would be given by simply summing the deflections measured by occupants of a series of elevators along that path, each in terms of their respective local coordinates.

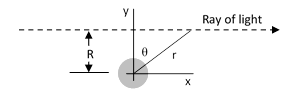
It’s interesting to compare how Einstein actually performed the light-deflection integrations in 1911 and 1915. In the derivation of 1911 he introduced the angle θ to parameterize the position of a wave crest as shown below.

Making use of the relations r = R/cos(θ), x = R tan(θ), r² = x² + R², and the differential relation dx = [R/cos(θ)²]dθ, the integral in the 1911 calculation can be written as

Oddly enough, Einstein actually wrote this as

where “s” is a length parameter along the path. This expression is equivalent to the integrals we’ve written if we identify “s” with x and make the other substitutions noted above. Nevertheless, Einstein’s expression contains a mixture of three or four different parameterizations for the path, namely s, θ, r, and (implicitly) x. Also, if “s” is not identified with x, we would need to account for the variation in y (implicit in r) along the path. By the time of his 1915 calculation (as described in the 1916 review paper), Einstein had dropped the θ and s parameters, and indicated a direct integration over x from negative to positive infinity, just as in our earlier presentation. Of course, he might still have introduced the θ parameter to actually evaluate the integral. Making the same substitutions as noted above, we can write the 1915 integration as

The derivation given in Einstein’s Princeton lecture in 1921 is the same as in the 1916 paper. He refers explicitly to the deflection of a light ray moving parallel to the x axis from negative to positive infinity, which confirms that his derivation was based on the “small deflection” limit. For a more general derivation, see Section 6.3.

The preceding discussion explains the meaning of Einstein’s oft-quoted comment in Appendix 3 of his 1916 book “Relativity”, where he states that “half of this deflection is produced by the Newtonian field of attraction, and the other half by the geometrical modification (‘curvature’) of space caused by the sun”. As explained in Section 8.5, Newton’s theory can essentially be expressed as a metrical theory with a line element given by (1), according to which the spatial geometry is flat, but curved in time. This leads to the Newtonian prediction 2m/R. The line element given by (2) includes the effects of spatial curvature, as indicated by the variable coefficients of the space-space components. As we’ve seen, when the effect of this spatial curvature is taken into account, the total predicted deflection is 4m/R.

Incidentally, after Einstein’s prediction of the deflection of light was (somewhat delicately) confirmed by the British solar expeditions in 1919, some of Einstein’s critics (notably Phillip Lenard) claimed that the very same deflection, i.e., twice the “Newtonian” value, had actually been predicted by Soldner in 1801. Now, Soldner’s computation was based entirely on Newtonian physics for ballistic light particles, which unambiguously gives half of the relativistic value, and indeed this is the numerical value that Soldner gave (i.e., 0.84 seconds of arc for a ray grazing the sun). The “extra” factor of 2 appearing in most of his formulas has been attributed to a mere difference in notation, since it was common in the German literature of that time to define the symbol for “acceleration of gravity” as half of the modern definition (e.g., the distance traversed by a dropped object in time t was written as gt² instead of (1/2)gt².) The fact that this extra factor was missing from some of the formulas was evidently just due to a printing error.

In a letter to Einstein, written in December of 1921, Hermann Weyl mentioned Lenard’s “unearthing of Soldner”, and says that he (Weyl) had taken the occasion to do some historical research:

I flipped through Newton once myself, because it appeared very probable that he knew about this consequence of his theory of gravitation and light. But he puts it highly cautiously; he had, of course, computed the deflection of a light ray that passes by the Earth, as I gather from one passage in the Opticks, to estimate, through comparison against the deflection of light at the boundary of a refractive medium, that in the latter case a force must be active that is as much as 10¹⁵ times as large as the Earth’s attraction; but he does not speak of the deflection of a light ray by gravity then, but of a body that is flying along at the same velocity as light.

What Weyl describes here is somewhat similar to the comments that Newton included in the Scholium at the very end of Book 1 of the Principia, quoted in the epigram of this note, although there Newton was referring more to the phenomenon of diffraction rather than refraction, and he makes no numerical comparison of the kind mentioned by Weyl, so it’s unclear what passage from the Opticks Weyl had in mind.

Return to Table of Contents