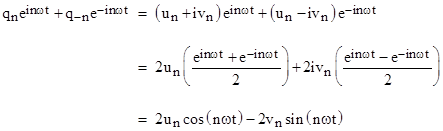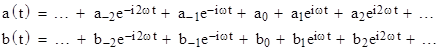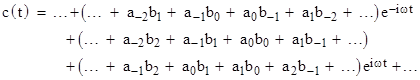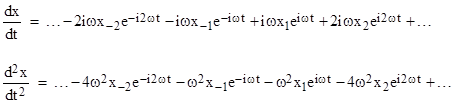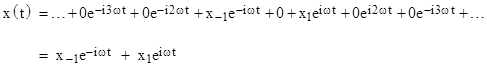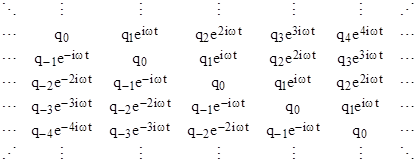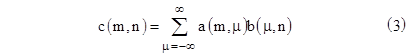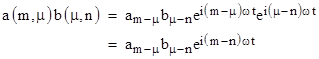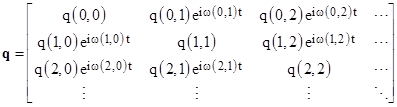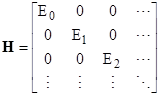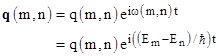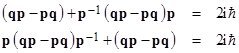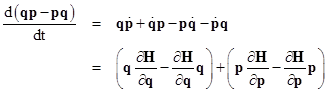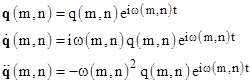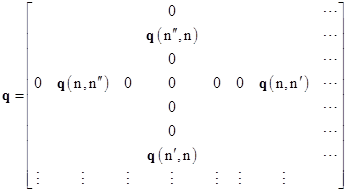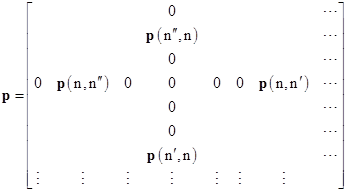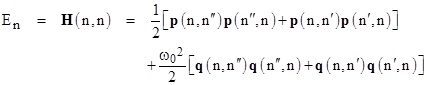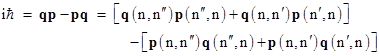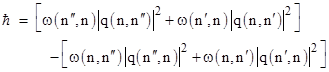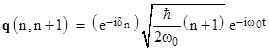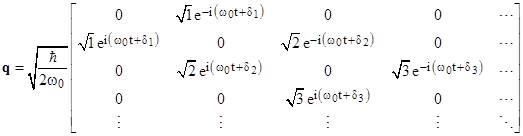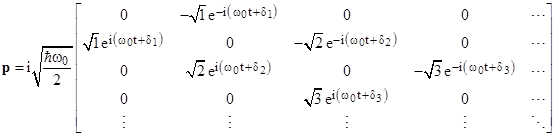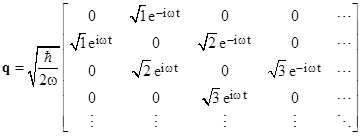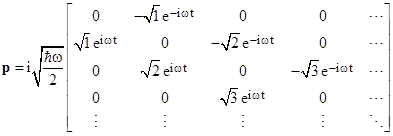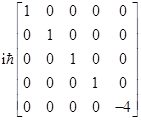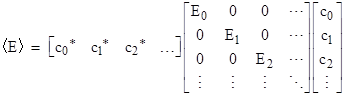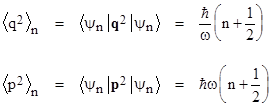On Matrix Mechanics

Introduction

During the early 1920s a virtual orchestra of physicists, including Einstein, Bohr, Born, Kramers, Slater, and Heisenberg, worked to resolve several difficulties with the (then) existing quantum theory. Finally, in June of 1925, seeking relief from a bout of hay fever, Heisenberg went to the pollen-free island of Helgoland (also called Heligoland) and invented what came to be called matrix mechanics, which was the first version of modern quantum mechanics. Heisenberg’s reasoning as he progressed from classical mechanics to “the fundamental equations of the new quantum mechanics” was not always perfectly clear. For some of the key steps he made use of the phrase “it seems that the simplest and most natural assumption would be…”, and then wrote down the quantum mechanical expression. Regarding this paper the great modern physicist Steven Weinberg wrote

I have tried several times to read the paper that Heisenberg wrote on returning from Helgoland, and, although I think I understand quantum mechanics, I have never understood Heisenberg’s motivations for the mathematical steps in his paper.

According to Weinberg’s account, Heisenberg in this paper was acting as a “magician-physicist”, i.e., one who “does not seem to be reasoning at all but who jumps over all intermediate steps to a new insight about nature.” Of course, Heisenberg himself acknowledged that his reasoning was not to be regarded as an axiomatic derivation. As he later wrote

It should be distinctly understood that this cannot be a deduction in the mathematical sense of the word, since the equations to be obtained form themselves the postulates of the theory. Although they are made highly plausible by the following considerations, their ultimate justification lies in the agreement of their predictions with experiment.

Nevertheless, it’s interesting to examine his considerations, to see just how plausibly they can serve as conceptual steps leading to the fundamental postulates of quantum mechanics.

From Series to Matrix

Heisenberg took as his starting point the classical description of a periodic physical system with variables written as Fourier series. For example, consider a physical system with a single degree of freedom, represented classically by the real-valued coordinate q, which we take to be a function of time. If the function q(t) is periodic with fundamental frequency ω = 2πν, we can express it as a Fourier series

where the coefficients q_n are complex constants representing the amplitudes of the respective frequency modes. In order for q(t) to be real-valued, each pair of amplitudes q_–n and q_n must be complex conjugates. In other words, if q_n = u_n+iv_n for real constants u_n and v_n then q_–n = q_n* = u_n–iv_n. This ensures that the sum of the two corresponding terms has the real value

Clearly any sums or differences of Fourier series of this form can also be expressed in this form, i.e., as real-valued Fourier series with the same frequencies, as can any derivatives of such expressions, noting that the coefficients corresponding to q_–n and q_n in the derivative of q are the complex conjugates iωu_n–ωv_n and –iωu_n–ωv_n. Furthermore, the product of any two functions of this form can also be written in this form. For example, given the two variables

where a_k and a_–k are complex conjugates, as are b_k and b_–k, the product c(t) = a(t)b(t) can be written as

Note that, as required, the coefficients of the nth and –nth terms are complex conjugates, because each product a_jb_k (where j+k=n) appearing in the nth coefficient is matched by the product a_–jb_–k in the –nth coefficient, and these products are complex conjugates in view of the identity x*y* = (xy)*.

To illustrate with a simple example in classical mechanics, consider a particle of mass m constrained to a single spatial dimension x and subject to a linear restoring force kx for some constant k. The kinetic energy of the particle is mv²/2 where v = dx/dt is the velocity, and the potential energy (found by integrating the force through the distance) is kx²/2, so the total energy at any time t is the sum

If the system is not emitting or absorbing any energy, then E is constant, and we could differentiate this expression and divide through by v to give

Assuming the coordinate x(t) is periodic with some fundamental frequency ω (still to be determined), we can write x in the form of a Fourier series as

Differentiating term by term, we also have

Inserting the series expressions for x and d²x/dt² into equation (2) and collecting terms, we get

The left hand expression must vanish for all t, so we must have x₀ = 0, and since ω is the fundamental frequency the coefficients x₁ and x_–1 must be non-zero (if any of the coefficients are non-zero), which implies that k – ω²m must vanish. Hence we have

With this value of ω, none of the other factors of the form (k – n²ω²m) can be zero, so it follows that all the other coefficients x₂, x₃, x₄, … and their complex conjugates must all be zero. Hence the solution must be of the form

where x₁ is an arbitrary complex constant and x_–1 = x₁*. The value of x₁ is typically determined by the initial conditions. The time derivative of x is the velocity

and hence the energy of the system, as given by equation (1), has the constant value

Thus the energy is strictly proportional to the linear restoring force constant. Of course, we have the relation k = mω². For later reference, we note that the average value (for any number of complete cycles) of the square of the position coordinate is <x²> = 2|x₁|², and the average value of the square of the velocity is <v²> = 2ω²|x₁|², so we have the relations <x²> = E/(mω²) and <v²> = E/m.

At this point we make note of the seemingly trivial fact that the components of the Fourier series of any given variable q(t) could be presented (albeit with needless extravagance and redundancy) by a doubly infinite array as shown below

Each row of this array contains the terms of the original series, and the rows are offset so that the constant terms q₀ are always on the main diagonal. Letting q(m,n) denote the element in the mth row and the nth column, we note that q(m,n) and q(n,m) are complex conjugates. Now, given the Fourier series for the variables a(t) and b(t) discussed above, the corresponding arrays have the components

Obviously we can add or subtract any two such arrays by simply adding or subtracting the corresponding components. Also we define the product of two such arrays so as to give the array corresponding to the product of the two series. It’s easy to see that if c(t) = a(t)b(t) then the component c(m,n) of the array corresponding to c is equal to the scalar product of the mth row of array a and the nth column of array b. In other words, we have

By construction, the c array has the same form as the original arrays, i.e., the phase factor of c(m,n) is e^i(m–n)t and the coefficients of the components c(m,n) and c(n,m) are complex conjugates.

Up to this point we haven’t made any substantive change in the classical representation of variables, we have simply duplicated the series components to create a two-dimensional array corresponding to each Fourier series. These arrays obviously have a great deal of redundancy, since each row is just a shifted copy of the elements of the original series.

However, a substantive change in this way of representing a variable now suggests itself. Notice that the phase factor associated with the coefficient q(m,n) has the frequency (m–n)ω, which is sufficient to ensure that the phase factors of any product of such arrays have the same frequencies, because, as can be seen from the above expression, the product c(m,n) is a sum of terms of the form

In other words, letting ω(m,n) denote the frequency of the phase factor associated with the coefficient q(m,n), we have the relation

Now, this relation obviously holds if ω(m,n) = (m–n)ω₀, for any given constant ω₀, but the same relation holds more generally. The necessary and sufficient condition is that there exist constants … ω_-2, ω_-1, ω₀, ω₁, ω₂, … such that

For the simple Fourier series the constant frequencies are just the integer multiples of the fundamental frequency ω₀, so the characteristic frequencies are taken to be simply …–2ω₀, –1ω₀, 0, 1ω₀, 2ω₀, …  However, we can just as well choose any sequence of frequencies we like, and still satisfy the requirement (4), although in general the resulting array will no longer correspond to a classical Fourier series. (The frequencies will no longer be the integer harmonics, and the rows of the array will no longer be just shifted copies of each other.)

Just as the phase factors need not be the same along each diagonal, the coefficients need not be the same either. All that is required to ensure consistency of the form of the arrays is that q(m,n) be the complex conjugate of q(n,m).

The extra flexibility permitted by condition (4) is just what’s needed to account for the observed spectra of atoms. Our classical discussion referred to the trajectory and fundamental period of the physical system in a stationary state, but when dealing with elementary particles no such trajectories or periods of stationary states are observed. Indeed, the very act of observation (or any kind of interaction) at the elementary level necessarily involves a change in the state of the system, i.e., from one stationary state to another, and we observe the frequency of the energy emitted or absorbed by the system. As Heisenberg said

It seems sensible to discard all hope of observing hitherto unobservable quantities, such as the position and period of the electron…  Instead it seems more reasonable to try to establish a theoretical quantum mechanics, analogous to classical mechanics, but in which only relations between observable quantities occur.

Thus the characteristic frequencies of an atom (for example) are the frequencies associated with changes from one energy level to another. It was already known to Heisenberg (from the experiments of Franck and Hertz on electronic impacts) that “the energy of an atom can take on only certain definite discrete values”, and that the frequency of radiation (emitted or absorbed) for a change from the energy level E_m to the energy level E_n is

where h is Planck’s constant. For any given sequence of energy levels …E_-2, E_-1, E₀, E₁, E₂, … this gives transitions frequencies that satisfy condition (4). However, atoms evidently have only positive energies, with an absolute lowest energy level, which we will call E₀. Hence we actually have just a singly-infinite sequence of energy levels E₀, E₁, E₂, …  Transitions involving negative indices are deemed impermissible, because they represent transitions to or from a state of negative energy, so we stipulate that all the array coefficients q(m,n) are zero if either m or n are negative. (In subsequent developments, leading to relativistic quantum field theory, transitions to and from negative energy states are unavoidable, but we are here considering only the original non-relativistic quantum mechanics.)

Taking all this into account, we arrive at a more suitable form for the variables of a physical system.

with the understanding that q(m,n) is the complex conjugate of q(n,m), and the frequencies satisfy relation (5) for some sequence of positive energy levels E₀, E₁, E₂, …, which ensures that ω(m,n) = –ω(n,m) and that relation (4) is satisfied. Letting the bold face q(m,n) denote q(m,n)e^iω(m,n)t, these conditions also ensure that q(m,n) and q(n,m) are complex conjugates, so the matrix q corresponding to the classical variable q is called Hermitian.

In his July 1925 paper, after introducing the matrix representation of quantum variables, Heisenberg originally deduced this rule for determining the square of a single variable, i.e., for multiplying a variable by itself, and then remarked

A significant difficulty arises, however, if we consider two quantities x(t) and y(t), and ask after their product. Whereas in classical theory x(t)y(t) is always equal to y(t)x(t), this is not necessarily the case in quantum theory.

He was worried about the (to him) strange feature of quantum multiplication, resulting from the rule for multiplying two quantum variables given by equation (3). Of course, it turned out that this non-commutivity was the essential key to the new quantum mechanics.

The Commutation Relations

At this point in Heisenberg’s original paper, as well as in the two subsequent papers by Born, Jordan, and Heisenberg, a “quantum condition” is established by analogy with the Wilson-Sommerfeld quantum condition of the old quantum theory. We discuss that thought process in a different article. Here we present instead a more direct line of reasoning leading to the same result.

Classically the Hamiltonian H(q,p) of a system (with one degree of freedom) represents the energy of the system expressed in terms of the coordinate q and momentum p. In quantum mechanics, as we’ve seen, q and p are represented by Hermitian matrices with characteristic energy levels and transition frequencies. Assuming the formal expression for the Hamiltonian in terms of q and p still applies, the Hamiltonian can therefore be expressed as such a matrix. As noted above the quantum condition implies a sequence of positive energy levels, and it is natural to define the quantum Hamiltonian H as the matrix representing these energy levels. If the energy is conserved we know that H is independent of time, so it must be a diagonal matrix (since all the off-diagonal terms have time-dependent phase factors). In that case we have

Now, recalling that the quantum coordinate q is given by a matrix with the elements

where , we have the time derivative

From this it is easily verified that

This shows the significance of the non-commutative property of matrix multiplication in the new quantum theory. At this point we postulate that the quantum variables satisfy the same Hamiltonian equations of motion as the corresponding classical variables, i.e., we have

where the partial derivative ∂H/∂p is defined as the limit of [H(q,p+εI) – H(q,p)]/ε as ε goes to zero, and thus has the same formal properties as ordinary partial differentiation. Substituting the left hand relation into the previous expression, we have

Furthermore, since q is independent of p, we have ∂q/∂p = 0, so we also have (trivially) the relation

Thus the relation

is valid at least for f = H and for f = q. As Born, et al, explained in their joint paper, it’s easy to show that if relation (6) holds for two matrices a and b, then it also holds for any sum and product of a and b, and therefore it holds for any matrix that can be expressed as a power series of those two matrices. Consequently relation (6) holds good for any matrix that can be expressed as a power series in H and q. At this point it is tempting to assert (as Whittaker does, for example) that since H is expressed as a power series in q and p, we can invert the relation and express p as a power series in H and q. However, H is generally a quadratic function of q and p, as in the case H = p²/(2m) + (k/2)q² for a harmonic oscillator. Solving for p in terms of H and q requires us to take the square root of a matrix (even if we expand the square root into a series), and it isn’t obvious that if (6) is valid for f = p² then it is also valid for the square root of f = p. To show that it is, we first note that if (6) is valid for f = p², then we have

Therefore, in view of the identity

we have

Multiplying through by the inverse matrix p^–1 on the left side or the right gives the two relations

Subtracting one from the other and multiplying through on the left by p and on the right by p^–1 gives

The left side is a similarity transformation, so this equation implies that qp–pq is “self-similar”. Obviously if qp–pq is a scalar matrix (defined as a scalar multiple of the identity matrix) then this equation is satisfied, but this equation by itself is not sufficient to imply that qp-pq is a scalar matrix. There exist “self-similar” matrices that are not scalar. However, if qp–pq is a diagonal matrix, as well as being self-similar, then it must be a scalar matrix. To prove that it is, in fact, a diagonal matrix, notice that we have the time derivative

Since the partial derivative of H with respect to q is purely a function of q, and obviously q commutes with itself, it follows that the quantity in the first parentheses vanishes, and similarly for the quantity in the second parentheses. Therefore the time derivative of qp–pq is zero, so it must be diagonal (since all the off-diagonal terms have time-dependent phase factors), and hence it is a scalar matrix. From equation (7) we then get the important result

The Quantum Harmonic Oscillator

The equation of motion for the harmonic oscillator is carried over from the classical case given by equation (2), except that the ordinary variable q is replaced by the quantum matrix q, so we have

In general the q matrix and its first and second derivatives with respect to time are

Therefore the equation of motion imposes the requirement

Consequently the only non-zero components q(m,n) must be those associated with a frequency ω(m,n) = ±ω₀. Heisenberg’s original paper made some unjustified assumptions as to the form of q, based on the correspondence principle, but in a follow-up paper Born and Jordan showed that, in fact, the form of the solution is fully determined (up to arbitrary permutations of the rows and columns) by the equation of motion and the quantum condition (8).

They first noted that each row (and hence each column) of q must have at least one non-zero term, because if the nth row (and nth column) of q was all zeros, the matrix given by qp – pq would have zero for the nth diagonal term, which would be inconsistent with the quantum condition (8). Furthermore, each row (and column) can have no more than two non-zero terms, since for any given index m there are only two possible roots E_j of the equation (E_m – E_j)² = ω₀², where E_n is the nth energy level, which is the nth diagonal element of the Hamiltonian, i.e., H(n,n) = E_n.

Now, for a unit mass the Hamiltonian function for a simple harmonic oscillator is

We’ve seen that, in general, the nth row and column contain at least one and possibly two (but no more) non-zero elements, so the nth row and column of p and q must be of the form shown below

Therefore, the nth diagonal of the Hamiltonian is

Since p = dq/dt for a harmonic oscillator, we have p(m,n) = iω(m,n)q(m,n), and therefore, remembering that that ω(m,n) = –ω(n,m), and that q(m,n) is the complex conjugate of q(n,m), and that ω₀² = w(m,n)², we have

Also, evaluating the nth diagonal of the quantum condition (8), we have

Simplifying again, this reduces to

Since ω(nʺ,n) = –ω(n,nʺ) and ω(n,nʹ) = –ω(nʹ,n), we can set ω(nʹ,n) and ω(n,nʺ) to +ω₀ (noting that those frequencies correspond to transitions from higher to lower energy) and write

If, for some index n₀, there is only one non-zero element in the n₀th row (and column) of q, then q(n₀,n₀ʺ) = 0 and equations (9) and (10) reduce to

and therefore

Since we assume that the energy levels for distinct states are distinct, this implies that there is only one row (and column) with a single non-zero entry. It follows that every other n there are precisely two other indices n’ and n”, and from the relation (E_n – E_j)² = ω₀² these indices must correspond to energy levels E_nʹ and E_nʺ, one above and one below E_n by the amount ω₀ . There can be only one such sequence, since there is only one index that has just a single “neighbor”. Consequently, setting n₀ = 0, the energy levels of the stationary states can be arranged in ascending order and assigned indices such that

With this assignment of indices, the only non-zero components of q are those adjacent to the main diagonal. Inserting the expression for E_n into equation (9), we can solve (9) and (10) to give

Remembering that q(n+1,n) is the complex conjugate of q(n,n+1), this relation determines the magnitude (i.e., the squared norm) of every non-zero element of q, but it doesn’t uniquely determine the elements themselves, because it leaves unconstrained a constant factor of unit magnitude and arbitrary phase angle δ_n for the nth complex conjugate pair. Thus for each index n = 0, 1, 2, … we have

and of course q(n+1,n) is the complex conjugate of this. It might be argued that factorization of the squared norm into its complex conjugate factors violates Heisenberg’s stated goal of establishing a quantum mechanics “in which only relations between observable quantities occur”, since, based on the conditions we have specified, the constant phase angles δ_n are completely arbitrary, and apparently have no observable effect. Nevertheless, they are formally part of the most general solution. Writing the matrix q explicitly, we have

Since p for this simple harmonic oscillator (with unit mass) is simply the time derivative of q, the “upper” elements of the momentum matrix are

and the “lower” elements p(n+1,n) are the complex conjugates of these. Writing the matrix p explicitly, we have

Of course, if by some interpretation the constant phase angles δ_n, implicit in every quantum variable, could be placed in correspondence with some observable effect(s), they might be considered as candidate “hidden variables”, but this is evidently not possible, and we will not pursue the idea here. According to the usual interpretation they are completely arbitrary and inconsequential, so without loss of generality we can set them all to zero, and we can also drop the subscript on ω₀ since there is only a single relevant frequency, and write the q and p matrices more succinctly as shown below.

When expressed as above, at t = 0 the components of q are purely real and those of p are purely imaginary. However, this has no absolute significance, because if (for example) we had chosen to set all the phase angles δ_n to –π/2 instead of zero, then at t = 0 the components of q would be purely imaginary and those of p would be purely real.

Discussion

It’s worth emphasizing that the matrices representing such quantum variables are necessarily infinite. This can be seen from the fact that the trace T(x) (i.e., the sum of the diagonal elements) of any finite matrix x is multiplicative, i.e., it satisfies the relation T(xy)=T(x)T(y) for any matrices x and y. Hence if q and p were finite matrices we would have T(qp–pq) = 0, which contradicts the quantum condition qp–pq = . For example, if we took just the first fives rows and columns of the q and p matrices presented above, then the matrix qp–pq would be

Likewise if we truncate the matrices at any finite number k of columns and rows, no matter how large, the component in the lower right corner of qp–pq will be –k+1, so the trace is always zero. The deviation from the required result increases without limit, so we cannot approach a valid solution by considering the limit of arbitrarily large finite matrices. It’s possible for matrices to satisfy the quantum condition (formally) only if the matrices are “actually” infinite (not just arbitrarily large), so that the lower right corner element (which represents the highest energy state, and whose value goes to infinity as the size of a finite matrix increases) does not exist. Aristotle, who rejected the intelligibility of the concept of “actual infinity”, would have been disturbed to learn that this is an essential aspect of the foundation of modern scientific theories. It’s interesting to compare this with the appearance of infinities in quantum field theory, and the technique of applying a high-frequency cutoff in order to achieve finite results. If the early quantum theorists had, for some reason, shared Aristotle’s aversion to actually infinite matrices, it’s interesting to consider whether they would have found some other way to justify neglecting the lower right hand element.

State Vectors and Probability

Subsequent to Heisenberg’s original paper in July of 1925, he wrote another paper with Born and Jordan, in which it was noted that if we have any two matrices q and p (such as the solution of the harmonic oscillator given above) that satisfy the commutation relation (8), then that relation is also satisfied by the similar matrices Q = SqS^–1 and P = SpS^–1 for any matrix S representing an arbitrary quantum variable. So, for a physical system with Hamilton H, if we can find a matrix S such that H(Q,P) = SH(q,p)S^–1 is diagonal, then the matrices Q and P will represent the stationary quantum mechanical solution of the system. Thus we can employ the usual method (as discussed in Complete Solutions of Linear Systems, for example), to effectively “integrate” the quantum equations of motion.

As discussed previously, the nth diagonal of the diagonalized Hamiltonian matrix H represents the energy level E_n of the nth stationary state of the system. This doesn’t tell us which particular energy level we should expect to find when we make a measurement. This will evidently depend on the state of the system, and yet the experimental results indicate that for a given “state” (prepared in as fully-specified a manner as we can) seems to lead to different measured values. Rather than being able to specify the single energy level of the system at any given time (as we could, in principle, do in classical mechanics), apparently each of the energy levels in the energy matrix H is a possible result of measurement, with a certain probability. Thus we have a set of probabilities p₀, p₁, p₂, … representing the probabilities of the stationary states with energy levels E₀, E₁, E₂, … respectively. Obviously we must have p₁ + p₂ + p₃ + … = 1, and of course the sum of the products p_jE_j equals the average energy level if we measured the energies of many systems in the same quantum state.

Accordingly, let us define the state vector ψ for a given system as a column vector of complex numbers c₀, c₁, c₂, … whose squared norms equal the respective probabilities. In other words, we have |c_j|² = p_j. If we then define the row vector consisting of the complex conjugates of c_j we can write the average value <E> of the energy for a diagonalized energy matrix H as

Following Dirac (as discussed in the article on Bras, Kets, and Matrices), it’s convenient to let |x> denote a column vector (called a “ket”) with the elements c_j, and let <x| denote the corresponding row vector (called a “bra”) with the complex conjugate elements c_j*. With this notation we can write the above as <E> = <ψ|E|ψ> where E signifies the diagonalized Hamiltonian. The probabilistic interpretation was first explicitly enunciated by Born, who showed that it gives a consistent prediction for the average value of any quantum variable. For example, with the harmonic oscillator discussed above, the average expected value of the position coordinate q is <q> = <ψ|q|ψ>. Note that the state vector here is constant, and the matrix representing the quantum variable is (in general) varying with time. This is called the Heisenberg picture, to distinguish it from the Schrödinger picture, in which the matrix representing the observable quantity is constant and the state vector varies with time. These are just two equivalent ways of expressing the solutions of linear systems, as discussed in the note on linear systems. The projection postulate can be applied to either picture. In the Schrödinger picture when a measurement is performed the state vector jumps to one of the eigenvectors of that measurement operator, represented by multiplying the state vector by a suitable projection operator. In the Heisenberg picture the projection operator is applied to the matrix representing the variable being measured.

Heisenberg’s original matrix mechanics didn’t include the concept of a “state vector”, nor did it describe the results of a “measurement”. The time-dependence of the quantum variables in the Heisenberg picture represents purely unitary evolution. However, as later formalized by von Neumann, when a measurement of some quantum variable is performed (which may be regarded as an interaction with a classical system), the result is one of the eigenvalues of the matrix representing that variable, and the state vector “jumps” to the corresponding eigenvector. This “jump” can be applied to either the variable matrix or the state vector (since only the combination is observable). Recall that for a given matrix M the eigenvalue λ and eigenvector v are defined such that . Thus when the matrix is in diagonal form, as is our Hamiltonian matrix above, the eigenvalues are the diagonal elements E₀, E₁, E₂, …, and the corresponding eigenvectors are |ψ₀> = (1,0,0,0…)^T, |ψ₁>= (0,1,0,0…)^T, |ψ₂> = (0,0,1,0…)^T, and so on. If we take ψ_j as the state vector, this represents the system being in the jth stationary state with the energy E_j. With this state vector we can also evaluate other variables of the system. For the harmonic oscillator discussed above, it’s easy to see that the average values of both q and p are zero for each of the stationary states (because the position coordinate and the momentum oscillate around zero). On the other hand, we would expect the squares of the position and momentum to have non-zero values, and indeed it’s easy to verify for the nth state that

Recall that, since this is for a particle of unit mass, the frequency ω equals the square root of the restoring force coefficient k (i.e., the “spring constant”). In view of equation (11), these equations imply <q²>_n = E_n/ω² and <p²>_n = E_n, in agreement with the classical oscillator discussed previously. As one would expect, for a given energy level, a stronger restoring force corresponds to a larger frequency and hence a smaller average squared distance from the origin.

Return to MathPages Main Menu