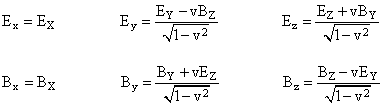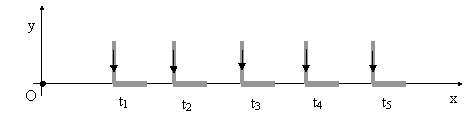Trouton-Noble and the Right-Angle Lever

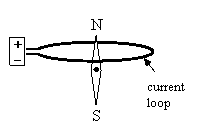
For many years during the early 1800’s the Danish physicist Hans Christian Oersted tried to find a connection between the forces of electricity and magnetism. His conviction that some such connection must exist was apparently based on his philosophical belief in the unity of the forces of nature. (He had written his PhD dissertation in 1799 on the philosophy of Immanuel Kant.)  In this respect Oersted was perhaps the founder of the modern scientific drive toward unification of the fundamental forces of physics. One of his experiments consisted of placing a loop of electric current around the magnetic needle of a compass as illustrated in the figure below.

He imagined that the current in the wire might somehow pull one of the poles of the compass needle toward it, but he found that this produced no deflection at all. However, in April of 1820, at the conclusion of one of his evening lectures, during which he had demonstrated this null result, he decided to try placing the coil in the North-South plane. Now, the prevailing conception of forces was that they are always exerted along the straight line between the inter-acting bodies, so placing the coil in the plane of the needle didn’t seem to be a very promising idea. After all, if both poles of the magnetic needle were already in the plane of the coil, how could the coil be expected to exert any deflecting force on the poles? Nevertheless, with just a few students remaining after the lecture, Oersted re-oriented the coil to the North-South plane, turned on the current, and made one of the most remarkable and important discoveries in the history of science. The magnetic needle suddenly turned to the East-West position, as depicted in the figure below.

Oersted had discovered the link between electricity and magnetism, but it was of a completely unexpected character. (This is strangely reminiscent of Bradley’s discovery of stellar aberration 90 degrees out of phase from the parallax effect he was expecting.) Oersted wrote

To the effect which takes place in the conductor and in the surrounding space we shall give the name of the conflict of electricity... It is sufficiently evident from the preceding facts that the electric conflict is not confined to the conductor, but dispersed pretty widely in the adjacent space. We may also infer that this conflict performs circles, for otherwise it seems impossible that the one part of the uniting wire, when placed below the magnetic pole, should drive it towards the east, and when placed above, should drive it towards the west, for it is the nature of a circle that the motions in opposite parts should have an opposite direction.

Interestingly, in his report on this experiment, Oersted emphasized that the effect was observed only when the circuit was closed (i.e., when current was flowing), not when the circuit was open, “as certain very celebrated physicists in vain attempted several years ago”. He didn’t identify those celebrated physicists, nor why they expected an open circuit to deflect a magnet, but perhaps they had in mind placing the magnetic needle between the plates of a capacitor. In any case, the comment highlighted the distinction between open and closed circuits, which had great significance in the later efforts of theoreticians to coherently represent the phenomena.

Oersted was suitably honored for his great discovery, but his conclusion about the character of the electromagnetic force was not immediately accepted by his contemporaries. In essence, he claimed that the force did not act along the straight line between the conducting wire and the poles of the magnetic needle. Instead, he suggested that, when current flowed in the wire, certain circular lines of force (or “conflict”) were established in the space surrounding the conductor, and it was these lines of force that drove the magnetic needle. This was the origin of the modern concept of a field… and it was also the beginning of the end of the simple mechanical view of physics.

To understand why this concept was so unexpected, and why it so fundamentally undermined the simple mechanical view, recall that Newtonian mechanics was based on the principle of action and re-action. Oersted was suggesting that the electromagnetic force was exerted on a material object (such as the compass needle) not directly by some other object, but by a “conflict” located in space. It isn’t clear how space itself can participate in the Newtonian action/re-action process, because (as far as one can tell) space has no mass and no identifiable state of motion. Two general approaches to this difficulty were pursued during the remainder of the 19th century. On the continent of Europe, most physicists tried in various ways to reconcile electromagnetic phenomena within the context of central forces and action at a distance, while in Britain attempts were made to incorporate Oersted’s “electrical conflict” into the mechanistic scheme by conceiving of it as a substantial aether filling all space.

Among those who continued to espouse the “direct action at a distance” approach to physics was the great French physicist Andre Marie Ampere, who analyzed the newly discovered electromagnetic phenomena by considering each small element of current individually. Ampere attempted to show that the phenomena were consistent with purely central forces of attraction and repulsion acting between these various parts of the current and the magnetic poles, and he partly succeeded, but only for situations involving closed current loops. Admittedly the force law he derived for the individual parts of the current (which we would call electric charges) involved a non-central component, but, when the total forces were integrated around a closed loop, the non-central components canceled out, so they could be regarded as just computational aids. Ampere believed that the non-central components would always cancel out, even in open loop situations, but it later became clear that this was not the case. The electromagnetic force (as classically defined) between two charges does not always point directly along the (instantaneous) line between the two charges. Thus, continuing with the “force at a distance” approach, Gauss and Weber found it necessary to postulate force laws that depend not just on the relative positions of the interacting particles but also on their relative velocities. At first the introduction of velocity-dependent force laws was criticized based on the belief that such forces must violate the conservation of energy, but it was later shown that Weber’s force law corresponded to a velocity-dependent potential which does conserve energy.

Meanwhile, in Britain, the idea of physical lines of force existing in space (rather than adhering to direct forces between distant material bodies) was taken up by Faraday, Kelvin, Maxwell, and others. Maxwell’s great synthesis of the laws of electromagnetism was completed by his introduction of what he called the displacement current, which he interpreted as signifying that all current loops are closed, thereby ensuring (in a sense) the very condition that is necessary for cancellation of the non-central components of Ampere’s “force at a distance”. However, Maxwell’s displacement current does not consist of observable material entities such as the charges moving along a conducting wire, but rather of changes in the state of the dielectric medium – even if the medium is the “empty space” of the vacuum. Thus Maxwell’s theory agrees with Oersted’s notion of a “conflict”, i.e., a field, in the space surrounding the conductors. The forces cannot be reduced to purely central force acting along the straight lines between the material objects… unless the apparent vacuum of space is endowed with some material substance. This hypothetical substance was called the aether (or ether), and much effort was devoted to the search for direct evidence of this substance, and to inferring its properties.

We see that both of the approaches to electrodynamics in the 19th century – Weber’s distant action theory and Maxwell’s field theory – attempted to account for Oersted’s fundamental discovery of non-central forces, albeit in different ways. Neither of the approaches was free of difficulties. The velocity-dependent potentials of Weber seemed to violate Newton’s third law explicitly, and Maxwell’s fields seemed able to avoid this violation only if the vacuum of space was filled with a substantial aether – a substance which could not be found and whose properties could not even be imagined, despite strenuous efforts. The field theory also raised troubling questions about the self-energy of electric charges residing in their own fields, which was not a difficulty for the distant action theory.

However, the field theory had one seemingly conclusive advantage, which was that, thanks to the displacement current and the presumed ability of empty space to support electric and magnetic fields, the theory predicted the existence of electromagnetic waves that would propagate through space at the speed of light. After Hertz demonstrated the transmission of electromagnetic waves in 1888, Maxwell’s field theory quickly became the predominant theory of electromagnetism, and remains so to this day. Nevertheless, it’s worth noting that the velocity-dependent potential of the distant action theory was subsequently modified by Leinard and Wiechert to incorporate a finite propagation speed (equal to the speed of light), and this retarded potential yields all the same observable phenomena as do Maxwell’s electromagnetic waves. Hence the field theory could no longer claim electromagnetic waves as unequivocal evidence in its favor, but by then the field theory – in the simple differential vector form given to Maxwell’s equations by Heaviside and others – had become firmly established.

Lorentz combined Maxwell’s field theory with a theory of the dynamics of charged particles (the newly discovered “electrons”) to give a fairly complete theory of electrodynamics by the beginning of the 20th century. This included what is now called the Lorentz force law

where q is the charge of the electron, E and B are the electric and magnetic field strengths at the location of the charged particle, and v is the velocity of the particle (in units such that the speed of light equals 1). Notice that this force equation refers only to a single material object (the charged particle) and to the components of the electromagnetic field at the location of the particle. Hence the force is not presented as being due to an interaction between two distant material objects, but rather as the response of a single object to the field at its location. Of course, the term involving the electric field E is easily seen to represent a central force, based on the idea that the electric field is spherically symmetrical centered on some neighboring charged particle. (As mentioned above, there are issues involving the effect of a particle’s own field on itself, but for sufficiently low speeds and accelerations these issues are arguably negligible.) However, the term involving the magnetic field B contains the cross product with the particle’s velocity, which many point in any direction, so in general the force on the particle need not be directed straight toward (or away from) the source of the field.

Remarkably, though, if two charges are each moving inertially (and have been for some time), the electric force on each particle points directly toward the present location of the other particle. This is interesting because, given that the potential effectively propagates only at the speed of light, one might expect the electric force to point toward the past position of the source particle, allowing for the time delay for propagation of the potential. However, the electric potential contains a velocity dependence that is precisely what is required to compensate for this propagation delay, resulting in a purely central force. In fact, this is sometimes used as an argument for why any force such as the electric force must have a velocity-dependent potential, assuming we accept that there is a limit for the speed of propagation of any force. This, in turn, leads to the necessity of a corresponding magnetic force, so Oersted’s philosophical notion that the electric and magnetic forces must be related had a rational basis after all.

But there remain some apparent difficulties for Newton’s third law in the context of Lorentz’s theory. First, as noted above, the velocity-dependent potential of the electric field yields a “central force” only for charges that are (and have been) moving inertially. If one or both of the charges undergoes acceleration, the compensation is no longer exact, and there are non-central forces on the charges. Poincare initially criticized Lorentz’s theory for this apparent violation of Newton’s third law, but by 1900 Poincare had noticed a possible way of reconciling the situation. When a charged particle is accelerated it emits electromagnetic radiation, and Poynting had shown that this radiation represents a flux of energy. Poincare showed that an energy flux S can be considered to correspond to a momentum flux S/c². This was an early and important step toward the recognition of the equivalence of mass and energy. Poincare showed that, when the momentum of the electromagnetic field energy is taken into account – along with suitable hypothesized motions of the unobservable aether – Newton’s third law is strictly satisfied.

Of course, this resolution commits us to accepting electromagnetic energy as one of the proper “objects” to which Newton’s third law applies, even though an electromagnetic wave (for example) is evidently not a material entity in the usual sense. Maxwell himself regarded this as one of the most compelling reasons for belief in a substantial field as the medium of electromagnetism, commenting that if we accept that an electromagnetic wave possesses energy and propagates at a definite finite speed, then the energy and momentum must exist in some form during the time after it has been emitted from one body and before it has been absorbed by another. Hence (he argued) we cannot avoid the conclusion that the field itself can embody energy and momentum, i.e., these are not properties of material bodies exclusively. In this regard, Planck pointed out that, in order to maintain the strict conservation of energy, it had been necessary several times to expand the concept of what qualifies as “energy”, so it shouldn’t be surprising that it was necessary to expand our idea about what qualifies as “momentum” in order to maintain strict conservation of momentum. On the other hand, Lorentz  wasn’t convinced that the principle of action and re-action needed to be saved. In a letter to Poincare in 1901 he wrote “But must we, in truth, worry ourselves about it?”

Incidentally, Poincare also noted that the velocity-dependence of the potential of the electric field (and the existence of the magnetic field) undercuts an argument made by Laplace, who had claimed that the force of gravity must propagate millions of time faster than light in order to avoid unacceptably large aberration effects on the orbits of the planets. Laplace’s reasoning didn’t take into account the possibility that gravity (like electromagnetism) might consist of a set of components that would compensate for the effects of mutual motions, and that the gravitational field components might convey both energy and momentum so that Newton’s third law would still be satisfied even in the presence of relatively small residual non-central forces.

Returning to Lorentz’s theory, there remained one source of concern related to Newton’s third law, even after accounting for the energy and momentum of electromagnetic radiation. The issue can most clearly be seen by considering a body in motion and subjected to stress. Just as in the case of electric currents, we find again an important distinction between open and closed “currents” of stress. If an unaccelerated object (or assembly of objects) is not subjected to any external force, then any internal currents of stress must be closed loops. For example, a compressed spring contained inside a rigid box represents a closed loop of stress, passing through the spring and then through the walls of the box back to the spring. Such closed loops of stress present no difficulty for Newton’s third law, regardless of the frame of reference in terms of which they are described. However, if a system is subjected to external open-loop stresses, the theory of Maxwell and Lorentz leads to some surprising predictions. An experiment performed by Trouton and Noble to test these predictions gave an unexpected result.

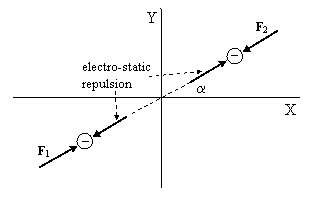
Reduced to the simplest terms, the experiment of Trouton and Noble can be understood as consisting of two negatively charged particles at rest relative to a system of inertial coordinates X,Y,T, and prevented from flying apart by the application of external forces inward on each of the particles, as shown below.

This stationary configuration presents no difficulties, since the force of repulsion between the particles acts directly along the straight line between them, and the two external forces F₁ and F₂ are also aligned on the same axis, with equal magnitudes in opposite directions. Since neither of the charged particles has any velocity, no magnetic force appears. Thus the electric and magnetic field strengths at the upper right particle are

Now consider the same situation in terms of a system of inertial coordinates x,y,t, such that the space axes are parallel to X and Y but moving in the positive X directions with the speed v. As explained in the article on Force Laws and Maxwell’s Equations, the components of the electric and magnetic field in terms of this relatively moving coordinate system are given by

Also, in terms of the xyzt coordinates, the particles are moving with the speed v in the negative x direction, so the velocity vector components are v_x = -v, v_y = 0, v_z = 0. Inserting these values into Lorentz’s formula (1) for the total electromagnetic force, we get

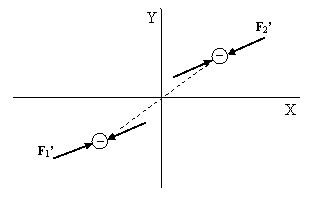
Consequently the Y component of the repulsion force exerted by each particle on the other is reduced by the factor (1-v²)^1/2 but the X component is unchanged, so those forces experience aberration as shown below, where we’ve also shown that the X component of the distance between the two particles has been reduced by the same factor, while the Y component is unchanged.

Both of these effects contribute to making the direction of the forces deviate from the straight line between the particles. As a result, we might expect an unbalanced torque to exist, causing the particles to revolve around their center of mass in the clockwise direction. The situation is essentially the same as in the experiment of Trouton and Noble, in which the two plates of a capacitor were suspended by a slender thread, with the expectation that the Earth’s velocity would cause aberration of the electromagnetic forces, leading to rotation of the capacitor. To explain the null result, Lorentz found it necessary to assume that the elastic forces holding the capacitor together were also electromagnetic, or at least that they transformed with velocity in the same proportion as do electromagnetic forces. This implies that, in terms of the translating coordinates, the external forces exhibit the same aberration as do the electromagnetic internal forces, so the net force on each particle remains zero, and hence the assembly does not rotate.

This is a logically consistent account, but it can be criticized in two ways. First, it is known that electromagnetism (being linear) cannot account for stable configurations, so the hypothesis that mechanical forces are ultimately electromagnetic in nature is not tenable. Hence Lorentz’s assumption that all forces of nature, including whatever non-electromagnetic forces are responsible for the stability of material configurations, transform exactly as do electromagnetic forces was purely ad hoc (tantamount to the assumption of special relativity). Second, the aberration of forces between particles raises again an apparent violation of Newton’s principle of action and re-action, albeit in a somewhat more subtle form. The individual couples of force evidently do not satisfy Newton’s principle, and yet in any closed-loop structure the non-central components cancel out, making the seemingly implicit violation of Newton’s principle unobservable.

As an aside, it’s interesting how closely this resembles the apparent violation of local realism involved in quantum entanglement. In both cases there is a correlation between pairs of separate but coupled entities, and the correlation, when considered in isolation, seems irreconcilable with any locally realistic flow of momentum, thereby seemingly implying a violation of relativity. And in both cases the overall circumstances conspire to preserve strict relativity, i.e., we find that (somewhat surprisingly) the non-classical correlations of momentum cannot be used to establish an absolute velocity.

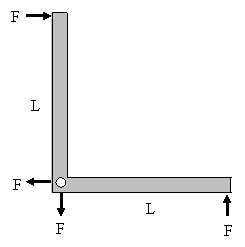
A few years after Lorentz gave his account of Trouton-Noble’s null result – an account that is also consistent with Einstein’s special relativity – the same basic phenomenon was given a stark representation in the form of a thought-experiment proposed by Lewis and Tolman in 1909. In their considerations of the effects of motion in special relativity, they were led to consider a “right-angle lever” with a pivot at the corner and equal forces F applied perpendicularly to the arms of equal length L, as illustrated below.

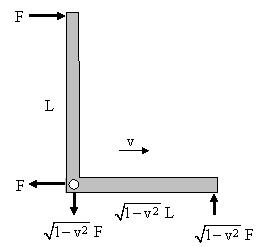
Since the lengths of the lever arms and the applied forces are equal, the lever is in equilibrium. Now we consider the same situation in terms of a coordinate system that is moving to the left at the speed v. In terms of this coordinate system the length of the vertical lever arm is still L and the force applied to this arm is still F, but the length of the horizontal arm and the magnitude of the force applied to this arm (according to the force transformation law we derived above) are both reduced by the factor (1-v²)^1/2, as shown below.

This is sometimes called the right-angle lever paradox, because (as in the Trouton-Noble experiment) there is evidently a net torque from the external forces on the lever which should cause it to rotate in the clockwise direction, and yet we know that the lever does not rotate (because it is in static equilibrium in terms of its rest frame). Oddly enough, when they first proposed this thought experiment in 1909, Lewis and Tolman were unaware of Lorentz had already given (in 1904) the relativistic force transformation law, as described above. In ignorance of this, Lewis and Tolman concluded that the transverse force must actually increase by a factor of (1-v²)^-1/2 (just the opposite of what Lorentz had shown) so as to make the external moments on their right-angle lever vanish.

Despite the original confusion of Lewis and Tolman, it’s clear that we can account for the lack of rotation of the lever in exactly the same way that Lorentz had explained the lack of rotation in the Trouton-Noble experiment, which is to say, by noting that all forces are Lorentz covariant, including the internal forces acting on the individual parts of the lever. It immediately follows that each part of the lever is subjected to null net force, both in terms of the original coordinate system and in terms of the moving coordinate system, so none of the parts undergoes any acceleration, and hence the lever does not rotate.

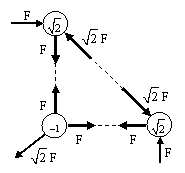
People are sometimes surprised that internal forces can produce a net torque, opposing the torque of the external forces. Indeed, if all forces are purely central, it can be shown that internal forces do not contribute to the torque on a body. However, as discussed above, relativistic forces are necessarily not purely central (in terms of arbitrary frames of reference), so they can and do represent non-zero net torques. It’s also worth noting that the distinction between “internal” and “external” forces is ambiguous, because it depends on our arbitrary partitioning between the system under consideration and the surroundings. For example, the right-angle lever can be succinctly represented by just three charged particles, two of one sign and one of the other, as illustrated below.

Each particle is subject to just three forces that sum to zero in terms of the rest frame of the particles, and since all forces transform in the same way, they also sum to zero when evaluated in terms of any other system of inertial coordinates. From the standpoint of each individual particle, all three of the forces are “external”, and hence there can be no objection to asserting that each particle is unaccelerated in terms of any system of inertial coordinates, and therefore the configuration of particles does not rotate. If, on the other hand, we regard the aggregate of all three particles as a single “object”, then the object is subject to three external forces which sum to zero with zero torque in the object’s rest frame, but which have non-zero torque when evaluated in terms of other reference frames. But we already know that the parts of this “object” are unaccelerated when the “internal” forces are taken into account. The physical effects of the forces between the charged particles does not change depending on whether we choose to examine the particles individually or as a group. The distinction between “internal” and “external” forces has no fundamental significance, especially since relativistic forces are generally not purely “central”.

Having said all that, it’s still legitimate to question whether non-central forces violate the principle of action and reaction. The answer to this question was provided by Max von Laue in 1911. As Pauli wrote in his 1921 article on relativity

As early as 1904, Lorentz gave the correct explanation that the elastic forces transform in precisely the same way as the electromotive forces. Laue’s conception goes deeper.

Laue’s deeper conception can be traced back to a paper written by Einstein in 1907 entitled “On the Inertia of Energy Required by the Relativity Principle”. (This is the paper in which Einstein made the somewhat notorious comment that as a young patent examiner he “felt I should be permitted to forgo a survey of the literature…”, since that could be relegated to the likes of Max Planck!) The first section of the paper is “On the kinetic energy of a rigid body in uniform translation subject to external forces”, wherein Einstein considers a rigid rod at rest in an inertial frame and subjected to equal and opposite compressive forces at its ends. In order to avoid accelerating the rod, the force must be applied simultaneously, but of course when described in terms of a coordinate system moving relative to the rod, the application of forces is not simultaneous. Instead, the force on the trailing end is applied first, followed by the application of the balancing force on the leading end. During the intervening time interval the force on the trailing end does work on the rod, and hence the kinetic energy of a moving rod under pressure is greater than that of the same rod in the same state of motion but free of pressure. Actually Einstein proved a more general result, covering all possible ways in which the forces could be applied to the rod, under the condition that there is no acceleration in the original rest frame.

We thus get the following strange result. If a rigid body on which originally no forces are acting is subjected to the influence of forces that do not impart acceleration to the body, then these forces—observed from a coordinate system that is moving relative to the body—perform an amount of work DE on the body that depends only on the final distribution of forces and the translation velocity. In accordance with the energy principle, from this it follows immediately that the kinetic energy of a rigid body subjected to forces is larger by DE than the kinetic energy of the same body moving at the same velocity but not subjected to any forces.

Now, once both the leading and trailing forces are being applied, the force on the trailing end continues to do work on the rod, but the same amount of work is being done by the leading end of the rod on the surroundings. As a result, in addition to the mass and kinetic energy of the rod itself, there is an energy current in the rod, consisting of the work done on the trailing end propagating up to the leading end. Moreover, in accord with the equivalence of mass and energy, this energy current also represents a momentum current. In the case of a linear rod with pressures parallel to the direction of motion and the axis of the rod, this momentum current is parallel to the velocity of the rod, just as in non-relativistic mechanics. However, von Laue realized that in other circumstances – such as the Trouton-Noble experiment or the right-angle lever – the momentum current associated with the application of forces on a moving body need not be parallel to the velocity of the body.

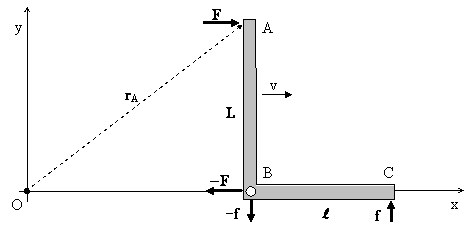
To understand how this comes about, and its consequences, consider again the right-angle lever and a coordinate system in terms of which the lever is translating to the right with speed v. We will assess the torques and angular momentum about the origin O of the coordinate system as shown below.

The magnitudes of f and l are (1-v²)^1/2. times the magnitudes of F and L respectively.  Letting r_A, r_B, and r_C denote the vector positions of the points A, B, and C on the lever, the net clockwise torque about the point O is given by

This net torque on the lever ought to equal the rate of change of angular momentum about the point O, and yet we know the lever is neither rotating about its fulcrum nor undergoing angular acceleration about the point O. It is simply translating to the right with respect to these coordinates, and maintaining its orientation. Now, we’ve already seen that the external torque is balanced by an internal torque (i.e., the elastic forces maintaining the shape of the lever itself) but, as Pauli said, there is a deeper explanation.

The force F applied to point A of the lever is acting through a distance as the lever moves to the right, so this force is doing work on the lever (and extracting work from the surroundings). Likewise the opposite force applied to point B of the lever is acting in the opposite direction of motion, so the lever is doing work on the surroundings. (The vertical forces at points B and C do not act through any distance, so they do no work.) This signifies that energy is being introduced at point A and removed from the lever at point B, so there is a flow of energy from A to B. Now we recall that the most profound implication of special relativity is the inertia of energy, i.e., the equivalence of energy and mass according to the relation m = E/c². Since we’ve chosen units such that c = 1, we have m = E. The rate at which energy is entering at point A (and departing at point B) is simply Fv, which we can regard as equivalent to a flow of mass. If each element of this flux moves from A to B at the speed u, the time required for the transit is L/u, and hence the total amount of this mass-energy in the lever arm at any given time is (Fv)(L/u). To get the total momentum of this mass-energy we simply multiply by the speed u, so the total momentum of the energy flowing from A to B is FLv. Thus as the lever moves to the right, there is a continuous current of momentum in the direction from A to B, as depicted below for a sequence of instants t₁, t₂, …

The angular momentum about the point O represented by this downward vertical flow of mass-energy equals the product of the momentum of the flow and the horizontal distance from O, so the angular momentum of the flow about the point O is (FLv)x in the clockwise direction. The horizontal position x is increasing at the rate v = dx/dt as the lever moves to the right, so the angular momentum of the system is increasing at the rate FLv², which is precisely equal to the net torque.

Oddly enough, even after the first self-consistent account of the Trouton-Noble experiment (and implicitly of the right-angle lever paradox as well) was given by Lorentz in 1904, and the more profound explanation was given by von Laue in 1911, there has been a steady stream of papers (albeit by individuals of modest attainments) claiming that one or both of those accounts are “wrong”. The authors of these papers argue about synchronous versus asynchronous explanations, internal versus external forces, kinematic versus dynamic effects, and about the relative merits of the various possible definitions of force and torque in a relativistic context. If nothing else, these papers give a nice illustration of the principle of action and re-action, since they spur endless rounds of papers and counter-papers, as each author helpfully explains why all others who have ever thought about the subject (including Lorentz, Poincare, Einstein, Sommerfeld, Laue, Pauli, etc) were misguided idiots. Typical among these papers is one by Butler (1969) in which we read that

In his efforts to explain the paradox, [Laue] invented the concept of the momentum of the “elastic energy current”. Laue made the ad hoc assumption that an elastic energy current exists from one end of the lever arm perpendicular to v to the other end of that same lever arm… Laue’s ad hoc postulate and its interpretations appear to raise more questions than they resolve. A few such questions are as follows: What kind of an instrument could one use to detect this elastic energy current in a laboratory?  What is the speed of this elastic energy along the lever? If the lever system is constantly increasing its angular momentum, what happens if after a long time this system collides with and sticks to another free body? Does all of this accumulated angular momentum show up in the rotation of the new aggregate system? How does one reconcile such an explanation with the principle of conservation of angular momentum?

It’s hard to see how the work done on and by the lever, and the resulting transmission of work (energy) from the one point to the other, can be regarded as an ad hoc assumption. And to disparage the insight that energy possesses inertia is nothing short of bizarre. Also, Butler’s innocence of the Poynting vector and the associated momentum flow in electromagnetic fields is obvious from his questions. One need only examine the fields involved in the configuration of the three charged particles discussed above to see explicitly the Poynting vector that appears when the electrostatic fields are transformed to mixed electromagnetic fields with respect to the moving coordinate system.

Those who argue about whether certain aspects of relativistic phenomena are “kinematic” or “dynamic” seem to overlook the fact that the inertia of energy (and the equivalence of mass and energy) renders that distinction obsolete. It could be said without much exaggeration that the whole message of special relativity is that kinematics and dynamics are just two different ways of describing the same things. A more meaningful distinction, and one that is often overlooked, is that between active and passive transformations. For example, the term “length contraction” as applied to a material object actually refers to two distinct concepts, depending on whether the physical object itself undergoes acceleration, or the object is simply described in terms of a different (relatively moving) system of inertial coordinates. This was emphasized by Einstein in the 1907 paper cited previously, in which he pointed out that the process of accelerating an object (even a seemingly “rigid” one) is actually quite complicated.

The effect of an impulse [on a body] is associated with a change of state of unknown quality in the body, which spreads throughout it with finite velocity and produces an acceleration of the body in a short time unless this effect is compensated by the effects of other forces acting upon the body within that time. Hence, if relativistic electrodynamics is correct, we are still far from having a dynamics of the parallel translation of the rigid body.

To avoid these complications we, for the most part, consider only unaccelerated objects described in terms of relatively moving coordinate systems, or else we condition weakly accelerated objects that can be regarded as being in quasi-static equilibrium.

In his 1909 book “The Theory of Electrons”, Lorentz acknowledged that whether all forces are ultimately electromagnetic in nature “remains an open question, about which we shall do well to speak with some reserve”, but he expressed his reasons for suspecting (as had Oersted a century earlier) a unity of all the forces of nature.

I believe every physicist feels inclined to the view that all the forces exerted by one particle on another, all molecular actions and gravity itself, are transmitted in some way by the ether, so that the tension of a stretched rope and the elasticity of an iron bar must find their explanation in what goes on in the ether between the molecules. Therefore, since we can hardly admit that one and the same medium is capable of transmitting two or more actions by wholly different mechanisms, all forces may be regarded as connected more or less intimately with those which we study in electromagnetism.

He was obviously mistaken in his belief that “every physicist” in 1909 was inclined to attribute all forces to “the ether”. (It’s interesting that he chose not to amend these words even in the 1915 edition.) Nevertheless, during the subsequent decades, quantum field theory succeeded in unifying the forces of electromagnetism and the strong and weak nuclear forces, vindicating – at least partially – the intuitions of Lorentz and Oersted. Only “gravity itself” has (so far) not been unified with the other forces.

Return to MathPages Main Menu