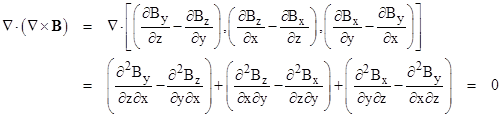Maxwell’s Displacement and Einstein’s Trace

There’s a remarkable parallel between Maxwell’s development of the field equations of electromagnetism and Einstein’s development of the field equations of general relativity. Recall that when Maxwell began his work there had already been established a set of relations describing the forces of electricity and magnetism. The earliest quantitative theories of electricity and magnetism were formulated in terms of forces acting at a distance, analogous to Newton’s law of gravitation. John Michell had shown in 1750 that the poles of stationary magnets exert on each other a force directed along the line between them with a magnitude inversely proportional to the square of the distance. Joseph Priestly (prompted by a suggestion from Benjamin Franklin) discovered in 1766 that the force of attraction or repulsion between stationary electrically charged particles is of this same form, a fact which was verified by Charles Coulomb in 1785. These discoveries, together with the success of the inverse-square law of gravity, led to the belief among most scientists that all the fundamental interactions of nature were to be understood in terms of inverse-square forces acting at a distance along the direct line of sight. However, in 1820 Oersted discovered that a moving charge (such as a current flowing through a wire) produces a magnetic force, and that this force evidently does not act along the direct line in sight. In 1830 Faraday discovered the reciprocal effect, i.e., that a moving magnet induces electric current in a wire. Ampere interpreted these effects, still within the framework of action at a distance, by formulating a force law that depended not just on the distance but on the velocity of the charged particles. Continuing with this approach, Gauss and Weber devised a fairly successful theory of electro-dynamics by the 1840s.

Beginning in the 1850’s, Maxwell elaborated ideas of Faraday to give a completely different account of electrodynamics, based on the concept of continuous fields of force. He showed that the inverse-square force laws of Michell and Coulomb can equally well be expressed in terms of such fields. In integral form, the flux of the field over any closed surface equals the charge enclosed within that surface. In differential form the same field law can be expressed by stating that the divergence of the field at any point equals the charge density at that point. Hence at any point free of charge the divergence of the field is zero. (Incidentally, from the absence of magnetic charges, i.e., mono-poles, it follows that the divergence of the magnetic field vanishes everywhere.) Maxwell also expressed the dynamical relations of Ampere and Faraday in terms of fields associated with moving magnets and electric charges. In all he arrived at a set of four partial differential equations, representing the laws of Michell, Coulomb, Ampere, and Faraday. All the information encoded in these four equations had been derived directly from experiment.

Maxwell then added another term to Ampere’s law, which he called the displacement current. The magnitude of this term was far too small to have been perceptible in the experiments performed by Ampere and Faraday, so its inclusion by Maxwell was motivated purely by theoretical considerations. Recall that Ampere’s original law, converted to differential form in terms of the magnetic field B, was

where j is the current density, understood to represent the flow of electric charge. Maxwell decided that this equation was incomplete, and the right hand side needed to be augmented by an additional term which he called the displacement current. His first published explanation of this term was really just a plausibility argument from a crude mechanical analogy, but in context it strikes me as a post facto rationalization rather than as a thought process that would have motivated the inclusion of the term in the first place. His explanation evolved over the years, as his ideas about suitable mechanisms changed, but in essence he argued that the current density j at a given location does not actually represent the total current flow at that location (even though that is essentially its definition). According to Maxwell, a dielectric medium can be considered to consist of couples of positive and negative charges, and an electric field E pulls these charges in opposite directions, stretching the links between them until they achieve some kind of equilibrium. If the strength of the field is increased, the charges are pulled further apart, so during periods when the electric field is changing there is movement of the electric charge elements of the dielectric medium. This movement of charge is what Maxwell calls the displacement current, proportional to ∂E/∂t, which he adds to Ampere’s original formula to give (in suitable units)

However, Maxwell’s rationalization of this extra term is questionable in at least two respects. First, it’s reasonable to ask why the displacement current is not already included as part of the total current density j at the given point. By definition, j is supposed to represent the flow of electric charge at a given location and time. Since Maxwell conceives of the displacement current as literally a flow of electric charge, one could argue that it should already be included in j, especially since the experimental results did not indicate the need for any additional term. Second, after introducing the concept of displacement current in dielectric media (where the existence of coupled electric charges is somewhat plausible), Maxwell goes on to apply the extra term to the vacuum, where the presence of coupled electric charges (being pulled apart and held in equilibrium by a stationary electric field) is questionable. He certainly could not point to any evidence of such disembodied charges existing in the vacuum. It’s true that some aspects of modern quantum field theory can be expressed in terms of pairs of oppositely charged virtual particles in the vacuum, flashing in and out of existence within the limits of the uncertainty principle, but surely virtual particles were not what Maxwell had in mind when he conceived of his tangible mechanistic models of the luminiferous ether. Without the uncertainty relations such particles would violate conservation of charge, a principle which Maxwell surely accepted. This principle can be expressed in differential form as

Now, recall that Coulomb’s law is ,  and if we take the partial of this with respect to time (and make use of the fact that partial differentiation is commutative), we get

Adding this to the previous equation gives

Thus the combination of charge conservation and Coulomb’s law implies that the divergence of equation (2) vanishes, whereas the divergence of equation (1) does not vanish. This immediately shows that equation (2) must be correct, i.e., we must add ∂E/∂t to Ampere’s law, purely for mathematical consistency, because the left hand sides of equations (1) and (2) are the curl of the magnetic field, and it’s easy to show that the divergence of the curl of any vector field is identically zero. Making use again of the commutivity of partial differentiation for an arbitrary vector field B, we have

It is sometimes argued that Maxwell’s addition of ∂E/∂t to Ampere’s law arose from his mechanistic model of the luminiferous ether, leading to the idea of a displacement current, and that this implies some kind of validity for that model. However, a review of his Treatise suggests a different interpretation. In Article 110, after discussing the hypothetical states of stress in a fluid dielectric, he says

It must be carefully borne in mind that we have made only one step in the theory of the action of the medium. We have supposed it to be in a state of stress, but we have not in any way accounted for this stress, or explained how it is maintained. This step, however, seems to me to be an important one, as it explains, by the action of the consecutive parts of the medium, phenomena which were formerly supposed  to be explicable only by direct action at a distance.

Thus Maxwell’s main concern was to formulate electrodynamics in such a way that it did not rely on action at a distance. The essence of his approach, following Faraday, was to treat the fields of force as having “consecutive parts”, and to regard the force as being communicated from one part to adjacent parts over time. In other words, his main commitment was to the idea of local action, not to the idea of a material mechanism for this action. Certainly a material mechanism would satisfy local action, but he was beginning to realize that local action need not imply a material mechanism. This is shown clearly when he then continues the discussion in Article 111 with an important admission

I have not been able to make the next step, namely, to account by mechanical considerations for these stresses in the dielectric. I therefore leave the theory at this point, merely stating what are the other parts of the phenomenon of induction in dielectrics…

When induction is transmitted through a dielectric, there is in the first place a displacement of electricity in the direction of the induction… Any increase of this displacement is equivalent, during the time of increase, to a current of positive electricity… and any diminution of the displacement is equivalent to a current in the opposite direction…

Thus the introduction of the displacement current (in Maxwell’s final presentation of his results) is prefaced by an explicit admission that he was not able to show how it would arise “from mechanical considerations for the stresses in the dielectric”. This applies even for a fluid dielectric, to say nothing of the vacuum. Admittedly he still refers to a displacement of electricity (i.e., a displacement of electric charge), but he follows this by saying “any increase of this displacement… is equivalent to a current”. This reveals Maxwell’s ambiguity, because if the displacement is actually a movement of electric charge, then it’s not just equivalent to a current, it is a current. Overall it seems fair to say that, even in his final presentation of the subject, Maxwell is unclear as to the nature of the displacement current.

One finds in the literature three basic justifications for introducing the “displacement current” term to Ampere’s law. First, it is sometimes claimed that it can be justified simply on the grounds of symmetry, i.e., since Faraday’s law indicates that a changing magnetic field is associated with an electric field, we would expect by symmetry that a changing electric field should be associated with a magnetic field. However, the glaring asymmetry due to the absence of magnetic monopoles tends to undermine the cogency of this argument. The second justification, found especially in historical treatments, is Maxwell’s heuristic rationale based on the idea of a dielectric medium consisting of charge couples that are pulled apart by an electric field. Lastly, the most common justification is consistency with Coulomb’s law and charge conservation, noting that the divergence of the curl of B must vanish. Thus we begin with Ampere’s hypothesis that the curl of B equals j, but then we note that the divergence of j does not vanish, whereas the vector  j + ∂E/∂t  does have vanishing divergence (due to Coulomb’s law and the conservation of charge), so we add this term to complete the field equations of electromagnetism in a mathematically and physically self-consistent way.

It’s interesting how similar this is to the process by which Einstein arrived at the final field equations of general relativity. The simplest hypothesis involving only the metric coefficients and their first and second derivatives, is that the Ricci tensor R_μν equals the stress energy tensor T_μν, but then we notice that the divergence of T_μν does not vanish as it should in order to satisfy local conservation of mass-energy. However, the tensor T_μν - (1/2)g_μνT does have vanishing divergence (due to Bianchi’s identity), so we include the “trace” term -(1/2)g_μνT to give the complete and mathematically consistent field equations of general relativity

which can also be written in the equivalent form

Just as the inclusion of the “displacement current” in Ampere’s formula was the key to a Maxwell’s self-consistent field theory of electrodynamics, so the inclusion of the “trace stress-energy” in the expression for the Ricci tensor was the key to Einstein’s self-consistent field theory of gravitation. In both cases, the extra term was added in order to give a divergenceless field.

Incidentally, to the three common justifications for the displacement current discussed above, we might add a fourth, namely, the fact that the inclusion of the term ∂E/∂t in Ampere’s equation leads to transverse electromagnetic waves propagating in a vacuum at the speed of light. Of course, this is ordinarily presented (triumphantly) as a consequence of the added term, rather than as a justification or motivation for it. However, someone as mathematically astute as Maxwell could hardly have failed to notice that the standard wave equation would result from the known system of electromagnetic equations if only Ampere’s law contained a term of the form ∂E/∂t. Indeed Faraday (Maxwell’s primary source and inspiration) had speculated that the electromagnetic ether and the luminiferous ether might well turn out to be the same thing, suggesting that light actually is a propagating electromagnetic disturbance. Also, Weber had shown that a speed on the order of the speed of light is given by a simple combination of electromagnetic constants, and many other people (including Riemann) had pursued the same idea. The objective of explaining the wave properties of light was certainly “in the air” at that time. Is it conceivable that Maxwell actually reverse-engineered the displacement current precisely so that the equations of electromagnetism would support transverse waves at the speed of light in a vacuum? If so, he would have been consistent with a long tradition, dating back to the ancient Greeks, of arriving at results analytically but presenting them synthetically.

Einstein commented on this question in a letter to Michele Besso in 1918. He was chiding Besso for having suggested (in a previous letter) that, in view of Einstein’s theory of relativity, “speculation had proved itself superior to empiricism”. Einstein disavowed this suggestion, pointing out the empirical bases for all the important developments in theoretical physics, including the special and general theories of relativity. He concluded

No genuinely useful and profound theory has ever really been found purely speculatively. The closest case would be Maxwell’s hypothesis for displacement current. But there it involved accounting for the fact of the propagation of light (& open circuits).

In other words, although the displacement current itself had never been directly detected, the hypothesis of such a current could be very directly connected to empirical phenomena. Likewise the atomic hypothesis and the kinetic theory of gases arose (according to Einstein) from the empirical equivalence of work and heat. Similarly in the case of general relativity he cites the empirical equivalence of inertial and gravitational mass. Ironically, Einstein was later seen as having succumbed to the very notion for which he had chided Besso. He seemed to encourage this impression himself when he said (in the Herbert Spenser lecture of 1933)

The creative principle resides in mathematics. In a certain sense, therefore, I hold true that pure thought can grasp reality, as the ancients dreamed.

Regarding Einstein’s long search for a field theory that would unify the gravitational equations with Maxwell’s electromagnetic equations, his old friend Max Born wrote

He had achieved his greatest success by relying on just one empirical fact known to every school boy. Yet now he tried to do without any empirical facts, by pure thinking. He believed in the power of reason to guess the laws according to which God has built the world.

Return to MathPages Main Menu