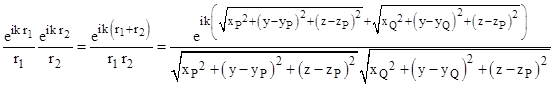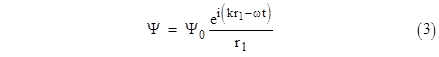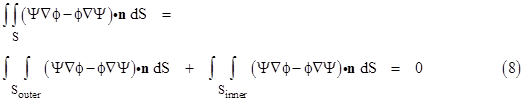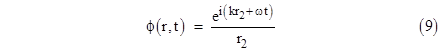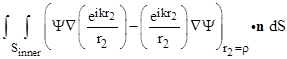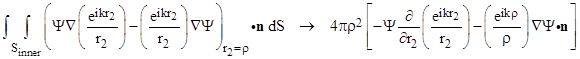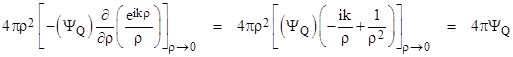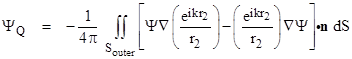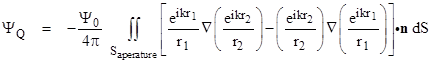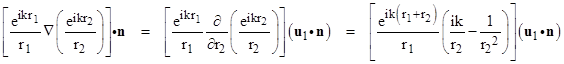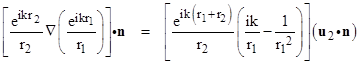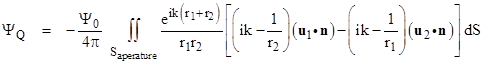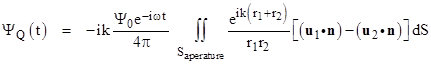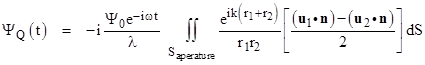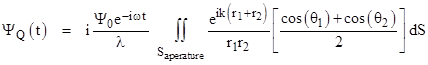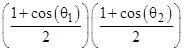On Diffraction

Why, I, in this weak piping time of peace,

Have no delight to pass away the time,

Unless to spy my shadow in the sun

And descant on mine own deformity...

                          Shakespeare, 1593

Able was I, ere I saw Elba.

                           Anonymous

We observe the effects of diffraction of acoustical waves whenever we hear a sound originating from (for example) behind a tree, so we’re accustomed to the fact that sound waves can propagate “around corners”, i.e., they aren’t constrained to propagate only in straight lines. On the other hand, visible light often gives the impression of propagating strictly in straight lines. We even speak about “rays” of light, and we don’t imagine that we can see around corners. The apparent rectilinear propagation of light led many scientists (such as Newton) in the 17th century to suspect that light consists of tiny corpuscles moving in straight lines through the vacuum of space. However, others (notably Huygens and Hooke) argued that light is a wavelike phenomenon, propagating in some medium. Based on the wave model, Huygens gave reasonable accounts of reflection and refraction of plane waves. His guiding principle was what is now called Huygens’ Principle, which asserts that each point on a wave front can be regarded as the source of a spherical wavelet, propagating at the wave’s speed at that location, and that the overall wave front at some future time is the envelope of tangency of all the wavelets. One might think this would imply diffraction effects, since we would expect the wavelets located at an aperture to spread out in all directions, but Huygens denied this, claiming that propagation of the wavelets proceeds only along a common front, perpendicular to the front. Hence (according to Huygens) a light wave does not turn around corners. He wrote in his Traite de la lumiere (Treatise on Light) in 1690

Each part of the wave is propagated in such a way that its extremities lie always between the same straight lines drawn from the luminous point. For instance, that part of the wave BG, whose centre is the luminous point A, develops into the arc CE, limited by the straight lines, ABC and AGE.

For although the secondary waves produced by the particles lying within the space CAE may spread to the region outside, nevertheless they do not combine at the same instant to produce one single wave, limiting the motion to the circumference CE which is their common tangent. This explains the fact that light, provided its rays are not reflected or refracted, always travels in straight lines, so that no body is illuminated by it unless the straight line path from the source to this body is unobstructed.

Thus, according to Huygens, diffraction is impossible. It’s interesting that although this passage is often cited as proof that Huygens never grasped the possibility of explaining rectilinear motion by interference, he actually does come close to invoking the concept of interference when he says “the secondary waves produced by the particles lying within the space CAE may spread to the region outside, nevertheless they do not combine at the same instant to produce one single wave”. Admittedly, this doesn’t show that he had any notion of destructive interference, but it does refer to a lack of constructive “interference” (i.e., of wavelets arriving at the same place and the same time to reinforce each other) as the reason that non-rectilinear propagation is suppressed.

There are several ironies in Huygens’ position. For example, he felt it necessary to truncate the wavelets at the boundaries of wave fronts in order to account for what he believed was the strictly rectilinear propagation of light, and then, having done this, he was unable to account for the phenomena of diffraction, which had been described by Grimaldi in a paper published in 1664. Once the wave theory of light was more fully developed, Huygens’ principle – minus the arbitrary truncation at the boundaries – was used to explain diffraction. But before this could be done successfully, it was necessary to extend that principle to include quantitative interference effects, and this in turn required a fundamental change in how “light” was conceived to be related to a “wave”. Descartes had taught that light consists of static pressure communicated instantaneously from the illuminated body to the eye, and, although Huygens replaced the static pressure with a transiently propagating wave, he evidently retained the idea that the sensation of light resulted from the static pressure that was (temporarily) produced when a single wave strikes the eye. This is quite different from the idea that the sensation of light is produced by oscillations of various frequencies, an idea that Huygens never espoused. Indeed Huygens never attributed a frequency or periodicity to his light waves. He conceived of light as a single pulse disturbance, and although he surely understood that there would be sequences of such pulses, he associated the sensation of light with each individual pulse, not with a sequence of pulses, i.e., not to oscillations.

Naturally this left him unable to explain the mechanism of color, an inability which he candidly admitted. He wrote in the preface to his Treatise

I trust there will be some who, from such beginnings, will push these investigations far in advance of what I have been able to do; for the subject is not one which is easily exhausted. This will be evident especially from those parts of the subject which I have indicated as too difficult for solution; and still more evident from those matters upon which I have not touched at all, such as the various kinds of luminous bodies and the whole question of color, which no one can yet boast of having explained.

It would be interesting to know how Newton reacted when, in the summer of 1689, Huygens visited London and presented his Treatise on Light at a meeting of the Royal Society. Although Newton did not publish The Opticks until 1703, he was well-known for having “explained” colors in a series of papers in the early 1670s, but it was not the sort of explanation that satisfied Huygens, who continued in the tradition of Descartes to always seek a mechanistic model (which Newton would have termed a hypothesis) for phenomena. According to Huygens

Demonstrations in optics, as in every science where geometry is applied to matter, are based upon experimental facts; as, for instance, that light travels in straight lines, that the angles of incidence and reflection are equal, and that rays of light are refracted according to the law of sines… Most writers upon optical subjects have been satisfied to assume these facts. But others, of a more investigating turn of mind, have tried to find the origin and the cause of these facts, considering them in themselves interesting natural phenomena. And although they have advanced some ingenious ideas, these are not such that the more intelligent readers do not still want further explanation in order to be thoroughly satisfied.

In case this wasn’t enough to make it clear that Huygens did not consider Newton to have said the last word on optics, Huygens continued

I have been astonished to find these same writers accepting arguments which are far from evident as if they were conclusive and demonstrative. No one has yet given even a probable explanation of the fundamental and remarkable phenomena of light, viz, why it travels in straight lines and how rays coming from an infinitude of different directions cross one another without disturbing one another.

This recalls the correspondence between Huygens and Newton (by way of Oldenburg) in 1673, when Newton had announced his results on the heterogeneity of white light and the different refrangibility of colors, and Huygens (after admitting that Newton’s ideas were “very ingenious”) had deprecated the achievement by pointing out that Newton had not provided any mechanistic explanation for colors. Newton replied

To examine how colours may be thus explained hypothetically is besides my purpose. I never intended to show wherein consists the nature and difference of colours, but only to show that de facto they are original and immutable qualities of the rays which exhibit them, and to leave it to others to explicate by mechanical hypotheses the nature and difference of those qualities, which I take to be no very difficult matter.

After Oldenburg forwarded this letter to Huygens (along with the comment that “Mr Newton is a man of great candor”), Huygens replied

Seeing that he maintains his doctrine with some warmth, I do not care to dispute.

In The Opticks Newton seemed to argue for a corpuscular theory of light, although he presented the idea only tentatively, and tried to avoid basing his factual findings on this or any other hypothesis regarding the mechanism of light. It is often said that the weight of Newton’s prestige and authority was responsible for the (temporary) abandonment of the wave conception of light during the 18th century, but this ignores the fact that a corpuscular theory has some definite strengths, and the wave conception has definite weaknesses. After pointing out difficulties which the wave theory has in accounting for numerous phenomena of electromagnetic radiation, Einstein wrote (in his 1909 paper “On the Development of our Views Concerning the Nature and Constitution of Radiation”)

The basic property of the wave theory that gives rise to these difficulties seems to me to lie in the following. While in the kinetic theory of matter there exists an inverse process for every process in which only a few elementary particles take part (e.g., for every molecular collision), according to the wave theory this is not the case for elementary radiation processes. According to the prevailing theory, an oscillating ion produces an outwardly propagated spherical wave. The opposite process does not exist as an elementary process. It is true that the inwardly propagated spherical wave is mathematically possible; however, its approximate realization requires an enormous amount of emitting elementary structures. Thus, the elementary process of light radiation as such does not possess the character of reversibility. Here, I believe, our wave theory is off the mark. Concerning this point the Newtonian emission theory of light seems to contain more truth than does the wave theory, since according to the former the energy imparted at emission to a particle of light is not scattered throughout infinite space but remains available for an elementary process of absorption.

In the same year (1909) Einstein discussed with Ritz (who espoused a classical emission theory of light) the origin of the temporal asymmetry in electromagnetism, i.e., why we observe retarded but not advanced waves, even though the latter are equally valid solutions of Maxwell’s equations, and again Einstein declared that the asymmetry was due to probability. Ritz, on the other hand, argued that the formal possibility of advanced waves in Maxwell’s equations indicated that those equations must be invalid, and should be replaced by equations that explicitly exclude advanced potentials. It’s interesting that both Ritz and Einstein came to distrust Maxwell’s equations, but for opposite reasons. Ritz thought those equations were wrong because they entail the formal possibility of reversible interactions, whereas Einstein thought they were wrong because they don’t entail direct reversibility of elementary interactions. In other words, for Ritz, the classical wave theory of electromagnetic radiation was too symmetrical, whereas for Einstein it was not symmetrical enough. Ritz was seeking the origin of the second law of thermodynamics in some explicitly time-asymmetry of the elementary laws, while Einstein expected those laws to be perfectly time-symmetric, just like the laws of elementary particle collisions, and he argued that in both cases the second law emerges from statistical considerations (presumably along the lines Boltzmann had described).

Before leaving Huygens, it may be worth mentioning that he commented specifically on one aspect of his “principle” that is often cited as a shortcoming, and one that was (allegedly) repaired by subsequent workers like Fresnel and Kirchhoff. This relates to the “backward” propagation of secondary wavelets, which would seem to be predicted by the original version of Huygens’ principle, raising again the issue of temporal asymmetry, and the question of why the outward propagation of a spherical wave exists as an elementary process whereas the reverse (i.e., the inward propagation of a spherical wave) apparently does not. It is often said that the resolution of this problem comes from Fresnel’s introduction of interference effects, or Kirchhoff’s derivation based on the scalar wave function, but both of these claims are questionable at best. When we consider the Fresnel-Kirchhoff theory of diffraction (below) we’ll see that the so-called “obliquity factor”, which effectively eliminates the backward-going waves (in forward time), is essentially introduced by fiat, so the absence of backward wavelets in the “modern” version of Huygens’ principle is (arguably) no more justified than it was in Huygens’ original statement. (He didn’t discuss the possibility of regarding the temporally-reversed incoming waves as the backward wavelets.) In his Treatise he wrote

From what has been said concerning the small intensity of the secondary waves, it would appear not to be necessary that all the ether particles [of the ethereal medium] be equal, although such an equality would favor the propagation of the motion. The effect of inequality would be to make a particle, in colliding with a larger one, use up a part of its momentum in an effort to recover. The secondary waves thus sent backward towards the luminous point would be unable to produce the sensation of light, and would not result in a primary wave similar to CE.

This isn’t a very satisfactory explanation, since it just pushes the alleged asymmetry down to the level of the particles of ether, where it still is given no intelligible justification. This may have been what led Huygens to the idea of an infinite regress of ethers (turtles all the way down), which he alluded to as follows

To apply this kind of motion to the explanation of light, nothing prevents our imagining the particles of the ether as endowed with a hardness almost perfect and with an elasticity as great as we please. It is not necessary here to discuss the cause either of this hardness or of this elasticity, for such a consideration would lead us too far from the subject. I will, however, remark in passing that these ether particles, in spite of their small size, are in turn composed of parts, and that their elasticity consists in a very rapid motion of a subtle material which traverses them in all directions and compels them to assume a structure which offers an easy and open passage to this fluid… So far from there being anything absurd or impossible in all this, it is quite credible that nature employs an infinite series of different-sized molecules, endowed with different velocities, to produce her marvellous effects.

Young and Fresnel didn’t pursue these rather speculative ideas of Huygens, but they did revive the wave theory of light, mainly by conceiving of light as an oscillation with a definite frequency (or mixture of frequencies), thereby accounting for colors, and also by proposing that light consists of a transverse (rather than longitudinal) wave, thereby providing a natural explanation for the effects of polarization. Of course, this also made it more difficult to represent light waves in mechanistic terms, but gradually the belief that mechanical processes were more fundamental (or inherently more intelligible) than electromagnetic processes was losing its persuasiveness. Eventually Maxwell’s great synthesis and completion of the laws of electromagnetism seemed to confirm that light was a transverse wave of high frequency, and on the basis of these equations it was possible to account for many aspects of the propagation of light, including the phenomena of diffraction and a modified form of Huygens’ principle – although not without some questionable assumptions and stipulations.

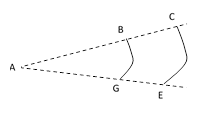
First, we should note that it isn’t difficult to arrive at a rough description of diffraction, especially in certain limiting cases. Consider the general case of a point-like light source A and another point B separated by an infinite partition containing a small aperture as illustrated below. (The width of the rectangular aperture in the perpendicular direction is taken to be arbitrarily small.)

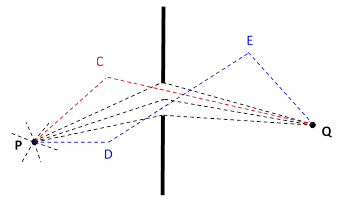
Even though the straight “line of sight” from P to Q is obstructed, there are still paths from P to Q, noting that each point on the spherical waves emanating from P is to be regarded as the source of secondary spherical waves. The most shortest and simplest wave paths are those that proceed rectilinearly from P to the aperture, and then rectilinearly from the aperture to Q. There are, of course, other two-step paths, such as the paths PCQ, and there are also three-step paths such as PDEQ, and so on, but we can get some idea of the expected behavior from just considering the paths that are rectilinear except at the aperture.

The light arriving at Q is the sum of the light from all possible paths, but accounting for the differences of phases, because the path lengths are different. The amplitude contributed by a particular light wave (along a particular path) at a distance r from the source can be represented by a function of the form

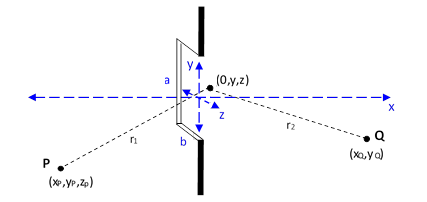
where k is the wave number (equal to 2π/λ where λ is the wavelength) and ω is the frequency. Since the waves are all synchronized, we need only consider the differences in spatial path lengths. The diagram below shows the parameters for determining the path length of one of the paths.

Again, the size of the aperture in the “z” direction is taken to be arbitrarily small, so we need consider only a single plane slice. The amplitude contribution of the indicated path is

Integrating this for positions of the intermediate point ranging over the entire aperture gives an approximation of the total amplitude. The squared absolute value of this integral gives an approximation of the intensity. This is essentially Fresnel’s theory of diffraction, according to which the intensity at point Q from a wave emanating from point P is

This is rightly called an approximation for several reasons. First, we are uniformly weighting the contributions in proportion to the area in the aperture, but this is only approximately correct, since the primary waves impinging on the aperture are oblique. Of course, if the aperture is small compared with the distances of P and Q from the partition, and if those points are not too far from the x axis, the angles of the rays will all be close to zero, so we can indeed neglect the obliqueness and simply integrate uniformly over the area, but in general this is only an approximation. Also, as Fresnel himself noted, Huygens’ principle in its primitive form assumes the secondary waves are equally strong in all directions, whereas Fresnel anticipated that those waves would be weaker in directions other than the direction of the primary wave. He wrote

Since the impulse communicated to every part of the primitive wave was directed along the normal, the motion which each part of the wave tends to impress upon the ether ought to be more intense in this direction than in any other; and the rays which would emanate from it, if acting alone, would be less and less intense as they deviated more and more from this direction. The investigation of the law according to which their intensity varies about each centre of disturbance is doubtless a very difficult matter; but, fortunately, we have no need of knowing it, for it is easily seen that the effects produced by these rays are mutually destructive when their directions are sensibly inclined with respect to the normal. Consequently, the rays which produce any appreciable effect upon the quantity of light received at any point P may be regarded as of equal intensity.

Naturally Fresnel discounted the possibility of a backward secondary wave, but he provided no rigorous justification for excluding it, beyond the above allusion to the directionality of the “impulse” of the primitive wave.

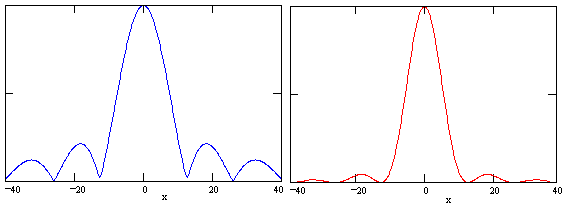
Despite the dubious aspects of this approach, it yields excellent results for a wide range of diffraction phenomena. The figures below show the amplitude and intensity for an aperture of 1 cm, wavelength of 0.02 cm, and distances of source and receiver from the aperture of 100 cm.

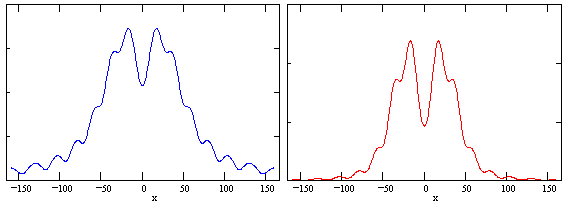
In this special case (which is called Fraunhofer diffraction) it can be shown that the intensity approaches the simple expression I = I₀ [sin(β)/β]² where β = ka x/(2D), a is the width of the aperture, and D is the distance from the aperture to the projection screen. On the other hand, for larger apertures (relative to the projection distances) the diffraction patterns are more complicated. For example, the figures below show the amplitude and intensity for an aperture of width 60 cm and a monochromatic light source of wavelength 0.8 cm for a light source (on the axis of the slit) at a distance of 200 cm from the aperture, projected onto a screen at a distance 200 cm from the aperture.

In this regime the results are known as Fresnel diffraction. Interestingly, Fresnel’s theory of diffraction based on the wave model of light was developed in 1816, when the corpuscular theory of light was still predominant. Indeed the major physicists of the day believed that the corpuscular theory could successfully account for all observed phenomena of light – with the notable exception of diffraction. Thomas Young had surely encountered great resistance to his efforts to revive the wave theory of light, as can be gathered from his comments in one of his early treatise:

The experiment of Grimaldi on the crested fringes within the shadow, together with several others of his observations equally important, has been left unnoticed by Newton. Those who are attached to the Newtonian theory of light, or to the hypothesis of modern opticians founded on views still less enlarged, would do well to endeavor to imagine anything like an explanation of these experiments derived from their own doctrines; and if they fail in the attempt, to refrain at least from idle declamation against a system which is founded on the accuracy of its application to all these facts, and to a thousand others of a similar nature.

Despite Young’s best efforts, the physics community in the first two decades of the 19th century continued to have confidence in the corpuscular theory. To overcome its last remaining obstacle, a contest was organized under the auspices of the French Academy of Science, with a prize to be awarded for the best paper on the phenomena of diffraction. Apparently the judges expected the final breakthrough in corpuscular theory but, alas, the only creditable entry was a paper (submitted in 1818) by Fresnel, in which he claimed to be able to model all diffraction phenomena based on the wave theory, specifically on the principle of Huygens combined with the effects of interference that had been described by Thomas Young. (Fresnel had devoted himself to the study of diffraction after losing his job for his part in the attempt to block Napoleon’s return from Elba in 1815.) One of the contest judges was Poisson, a staunch believer in the corpuscular theory of light, and a sharp critic of the wave theory. In his review of Fresnel’s paper, Poisson applied Fresnel’s theory to the case of the shadow cast by an opaque circular disk, and showed that – if Fresnel’s theory was correct – there should actually be a bright spot in the center of the circular shadow, directly behind the center of the disk, with intensity approaching what would be present at that location if the disk were entirely absent! Poisson apparently thought this should be sufficient to discredit the theory, but another of the contest judges, Arago, arranged for an experiment to test the prediction, and found the bright spot in the center of the shadow, just as the theory predicted. Fresnel was awarded the prize… and within just a few years the corpuscular theory of light had been totally abandoned in favor of the wave theory of Young and Fresnel.

Of course, Fresnel’s analysis of diffraction was based heavily on Huygens’ principle, the theoretical basis of which was unclear. A more rigorous treatment of diffraction, based on the Maxwell-Hertz equations for electromagnetic waves rather than on Huygens’ principle, was developed by Kirchhoff. This derivation, like Fresnel’s, still involves some approximations and physically questionable assumptions, but it has proven to be quite successful. Unfortunately the derivation is usually presented in a garbled form, obscuring the actual physical content.

We first assume the amplitude of the field oscillations emanating from point P satisfies everywhere (except perhaps on the surface of the partition) the wave equation

for some constant c with units of speed. Furthermore, we assume that, at every point up to the plane of the partition (including every point on the source side of the aperture), this scalar amplitude Ψ is a spherical wave emanating from the source P, i.e., the light field on the source side of the partition is of the form

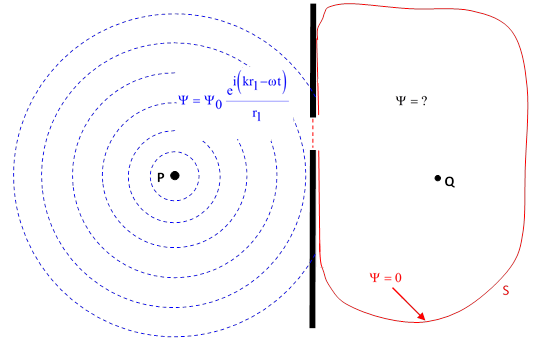
Of course, it’s easy to verify that (3) satisfies the wave equation (2) with c = ω/k. Our objective is to “extrapolate” this function through the aperture to the other side of the partition, to determine the value at the receiving point Q, as indicated in the figure below.

To the right of the partition we know only that the values of the scalar field Ψ on the surface of the aperture (shown in red) have the values given by the spherical wave function on the left side (shown in blue), and we know that Ψ satisfies the wave equation (2) for all points except possibly on the surface of the partition itself. In addition, we now assume that Ψ = 0 on the right side of the partition surface, and we also assume that we can enclose the receiving point Q in a closed surface S that is far enough from P so that Ψ is essentially zero over the entire surface.

Based on these assumptions, the value of Ψ at any receiving point Q is completely determined. We first recall the divergence theorem

where F is any continuous vector field over the region of interest. This signifies that the integral of the divergence of F over any enclosed volume equals the integral, over the enclosing surface, of the components of F normal to the surface. Many other useful identities can be derived from this simply by substituting various expressions for the vector field F. For example, consider a vector field defined in terms of two continuous scalar fields G and H as follows

In words, this means we define F as G times the gradient of H, minus H times the gradient of G. Substituting this into the divergence theorem, we get

Now suppose we specialize this theorem to the case where both of the scalar fields G and H satisfy the wave equation of the form (2). We can then substitute from the wave equation for the Laplacians on the left side to give

Now we specialize even further by considering only functions G and H whose second partial derivative with respect to time are, at every point, in the same proportion to G and H respectively. In other words, we require

which implies that the left hand integral vanishes. Thus, for any two scalar functions that each satisfy the wave equation (2) and the time-dependence condition (4), we have

We will show below how to use this equation to determine the amplitude of the scalar wave function Ψ at the location of the reception point Q, but first we must make a physical assumption about the form of Ψ. Recall that we assumed, for the region to the left of the partition, this function is given by

Thus at any given spatial position r₁ the function undergoes a simple oscillation with a frequency ω. This applies throughout the region to the left of the partition, but we now assume that it also applies to the region on the right of the partition. Whether we are really justified in assuming the wave function, after passing through an arbitrary aperture, continues to have a purely sinusoidal form with frequency ω at each point is questionable, but this assumption is required in order to carry through Kirchhoff’s derivation.

Now, notice that, for any function of the form

we have

Thus any function ϕ of the form (6) is compatible with our wave function Ψ in the sense that they satisfy equation (4) when substituted for G and H. If, in addition, the function ϕ is continuous and differentiable in the region of interest (i.e., the region enclosed by the red boundary in the preceding figure), and if it satisfies the wave equation (2) with c = ω/k throughout this region, then Ψ and ϕ also satisfy equation (5) when substituted for G and H. Thus we would have functions such that

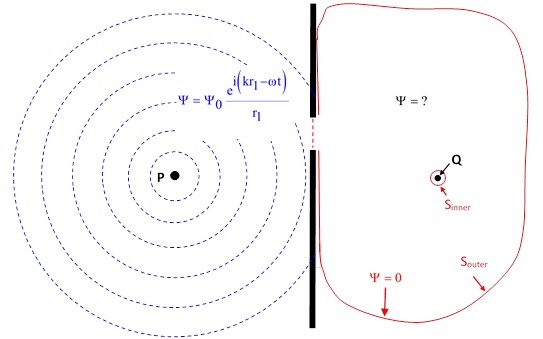
However, it isn’t clear how this relation leads to a determination of the amplitude of Ψ at the receiving point Q. It merely asserts that the integral of a certain quantity over the surface S equals zero. To find the amplitude of Y at Q, we make use of an interesting technique, based on the fact that we can enclose a region of space “within” a surface S consisting of two disconnected parts. In particular, we can apply (7) to a region that is enclosed between an outer surface S_outer and an inner surface S_inner, and we can choose the inner surface to surround the receiving point Q as shown in the figure below.

Applying equation (7) to the region enclosed between the inner and outer surfaces, we must integrate over both surfaces, so we have

Thus we have a relation between an integral over the outer surface and an integral over the inner surface, and we can make the inner surface approach as nearly as we like to the point Q. To make the evaluation of the inner surface integral as simple as possible, we choose a spherical surface of radius ρ centered on the point Q, and we also choose a function ϕ that is spherically symmetrical about the point Q. Recall that ϕ can be any function we choose, provided it satisfies the wave equation and has a time dependence of the form e^±iωt at each point and is continuous and differentiable throughout the enclosed region. A function that satisfies all these conditions, and that is spherically symmetrical about the point Q, is

where r₂ is the distance from the receiver point Q. Admittedly this function is singular at the point Q, where r₂ = 0, but the point Q is not contained with the region enclosed between the inner and outer surfaces. Now, we can factor the time dependence out of both Ψ and ϕ (since the factors e^±iωt are constants at any given instant, and each term in the integrals contains each time dependence), so we need consider only the spatial parts of the functions. Thus the integral over the inner surface (i.e., at r₂ = ρ) is

If we choose ρ small enough, the functions and their gradients will be essentially constant over the spherical surface, do we can simply multiply their values at the point Q by the sphere’s surface area 4πρ², which gives

We are applying the dot product with the normal vector n only to the gradient of Ψ, because the gradient of ϕ is always normal to the spherical surface, so the dot product of that term is simply the magnitude of the negative gradient, i.e., the negative partial of ϕ with respect to r₂. (We take the negative because n always points outward from the enclosed region, and hence it points inward toward Q, i.e., in the negative r₂ direction.) Notice that when we multiply through by 4πρ² the second term ends up with a factor of ρ in the numerator, so it vanishes in the limit as ρ goes to zero. Therefore, in that limit, the integral over the inner surface reduces to

where Ψ_Q is the value of the scalar amplitude of the wave function at the point Q. Substituting this for the inner integral and inserting the expression for (the spatial part of) ϕ into equation (8), we get

We’ve already stipulated that Ψ is zero over the entire outer surface, except for the aperture, where it has the values given by (3). Therefore, substituting the spatial part of (3) and noting that the integration need only extend over the surface of the aperture, we can re-write the above equation as

Since Y and f are both spherically symmetrical (about the points P and Q respectively), their gradients obviously point radially outward from their centers, and the gradients can be expressed as partial derivatives with respect to the radii. Thus the first term in the integral can be written as

where u₁ is the unit vector pointing in the direction of r₂. Likewise the second term in the integral can be written as

Inserting these expressions into the last expression for Ψ_Q gives

Recalling that the wave number k equals 2π/λ where λ is the wavelength of the (assumed monochromatic) light source, we see that in nearly all cases of interest the magnitude of ik is much greater than 1/r₁ and 1/r₂, so we can neglect the latter terms inside the square brackets and factor ik from the remaining terms. We can also multiply the entire expression, which represents just the spatial part of the wave, by the factor e^-iωt, which is the temporal part of Ψ. This results in the following expression for the time-dependent value of the scalar amplitude Ψ at the point Q:

Replacing k with 2π/λ and bringing one factor of 2 inside the integral, this can also be written in the form

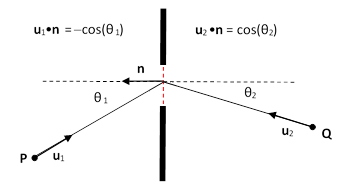
This is called the Fresnel-Kirchoff diffraction formula. The factor of –i signifies that the diffracted wave is 90 degrees out of phase from the original wave. The intensity is just the squared magnitude of the amplitude. Notice that the above is nearly identical to the result (1) which we got by the naïve application of Huygens’ principle, the only difference being the so-called obliquity factor [u₁•n – u₂•n]/2, which seems to vindicate Fresnel’s remarks (quoted above) about the variation in intensity of the secondary wavelets with direction. Remembering that n points outward from the aperture back toward the source P, we can express the dot products as cosines of the angles θ₁ and θ₂ as defined in the figure below.

Expressing the obliquity factor in terms of the cosines of these angles, we get

The symmetry of this equation is obvious, so it shouldn’t be surprising that the result is symmetrical, i.e., the fraction of the light from P reaching Q is the same as that for the light from Q reaching P. This palindromic property seems to be characteristic of the elementary processes of radiation, consistent with Einstein’s remarks about reversibility noted above.

The precise form of the obliquity factor is slightly puzzling, because it suggests that the contribution of a particular ray from point P to the aperture and from there to point Q depends not just on the angular difference between those two segments, but on the relation of each segment to the normal of the boundary in the aperture. If we chose a different surface to cover the aperture, but still including the point of the original aperture surface, the resulting contribution of the same rays to the same points would be different. This may be related to the lack of certainty in how much latitude (if any) we have when choosing the aperture surface. One sometimes sees the surface curved so that it is a constant distance from some point on the axis, and it is still assumed that the spherical form of the wave function extends to that surface. It might be suggested that this simple form exists at every point that is on a direct line of sight from the source, but this cannot be the case, because the receiving point itself could be in the direct line of sight of the source, and yet we know there are diffraction effects at that point. Thus there is clearly a limit to how far we can legitimately extend the aperture-covering surface and still claim that the wave function has the simple spherical form on that surface. In fact, even with the surface in the plane of the partition, it can be argued that this assumption is not strictly valid. Hence the precise form of the obliquity factor may be somewhat questionable. From an empirical standpoint, recall that Fresnel’s theory was eminently successful at reproducing the observed phenomena, and it completely omitted the obliquity factor (except perhaps for the exclusion of backward wavelets). On the other hand, the obliquity factor for the case of r₁ normal to the aperture surface is [1+cos(θ₂)]/2, which seems right from a quantum mechanical standpoint, and for this to be symmetrical, the general factor would either need to be as given in the Fresnel-Kirchoff formula or else (perhaps) by something like

which agrees quite closely with the former as long as either θ₁ or θ₂ is not very far from zero.

But in any case, the obliquity factor emerging from such an analysis can’t be regarded as the “explanation” for why we have forward (outward) propagating waves and not backward (inward) propagating wave fronts. Kirchhoff's solution is based not just on the assumption that the amplitude satisfies the wave equation, but on the assumption that the

amplitude is one particular solution of the wave equation, namely, an expanding spherical wave. Of course, there exist other possible solutions of the wave equation, such as an inward contracting spherical wave, which is precisely what Huygens' backward wavelets would produce. Hence we cannot exclude them merely by invoking the wave equation. We exclude them in Kirchhoff’s derivation by fiat, i.e., by stipulating at the start that the solution has the form of an outwardly expanding wave, at least up to the aperture surface. Furthermore, the derived solution applies only to the amplitude at points beyond the aperature surface, so it deals only with forward-going waves. The obliquity factor does indeed give 0 if we insert an angle of π (representing a wave emanating backwards from the aperture surface), but this is simply the value required for consistency with our assumption that the wave function up to the aperture surface is an outwardly expanding spherical wave. If we were to consider a receiving point Q on the source side of the aperture surface, it would be in the region where the wave function has simply been defined as an expanding spherical wave. Therefore, it is questionable to claim that the Fresnel-Kirchhoff theory with its obliquity factor "explains" why there are no backward-propagating waves. In his original treatment of the subject, Huygens referred vaguely to the momentum in the forward direction being greater than in the backward direction, but he couldn’t express precisely how a wave conveys momentum. This was greatly clarified by Poynting, who derived the energy and momentum flux of electromagnetic fields and waves.

Interestingly, although the reasoning of Fresnel and Kirchhoff leads to this very successful formula, the same results can also be derived in several different ways, based on completely different conceptions of what is actually happening. Indeed, Young had originally proposed the idea that diffraction effects arise from combining the directly transmitted waves with waves that are generated at the edges of diffracting objects. In a sense, it was an early form of the “absorber theory” of Feynman and Wheeler, because Young imagined that waves emanate only from material sources, in contrast with Fresnel’s view based on Huygens principle, according to which waves emanate from every point in a wave. After Fresnel’s brilliant success, Young discarded his “edge reflection” theory and endorsed Fresnel’s ideas, but many years later it was found that Young’s original theory of edge effects was actually valid, i.e., it actually is possible to decompose diffracted light patterns into direct waves from the source and edge-reflected waves, without resorting to the Huygensian notion of secondary wavelets originating at every point in empty space. On the other hand, Huygens’ principle is arguably more consistent with the “some over all paths” interpretation of modern quantum electrodynamics, which of course combines both corpuscular and wavelike features.

Return to MathPages Main Menu