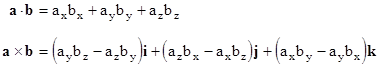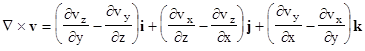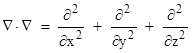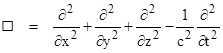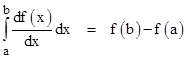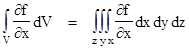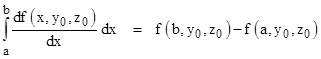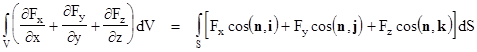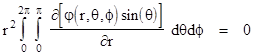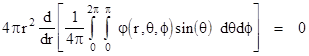Differential Operators and the Divergence Theorem

One of the most important and useful mathematical constructs is the "del operator", usually denoted by the symbol ∇ (which is called "nabla"). This can be regarded as a vector whose components in the three principle directions of a Cartesian coordinate system are partial differentiations with respect to those three directions. Of course, the partial differentiations by themselves have no definite magnitude until we apply them to some function of the coordinates. Letting i, j, k denote the basis vectors in the x,y,z directions, the del operator can be expressed as

All the main operations of vector calculus, namely, the divergence, the gradient, the curl, and the Laplacian can be constructed from this single operator. The entities on which we operate may be either scalar fields or vector fields. A scalar field is just a single-valued function of the coordinates x,y,z. For example, the static pressure of air in a certain region could be expressed as a scalar field p(x,y,z), because there is just a single value of static pressure p at each point. On the other hand, a vector field assigns a vector v to each point in space. An example of this would be the velocity v(x,y,z) of the air throughout a certain region.

If we simply multiply a scalar field such as p(x,y,z) by the del operator, the result is a vector field, and the components of the vector at each point are just the partial derivatives of the scalar field at that point, i.e.,

This is called the gradient of p. On the other hand, if we multiply a vector field v(x,y,z) by the del operator we first need to decide what kind of "multiplication" we want to use, because there are two different kinds of vector multiplication, commonly called the dot product and the cross product. For two arbitrary vectors a = a_xi + a_yj + a_zk and b = b_zi + b_yj + b_zk the dot product a·b and the cross product a×b are defined as

Intuitively, the dot product is a scalar equal to the product of the magnitudes of a and b times the cosine of the angle between them, and the cross product is a vector perpendicular to both a and b (with direction determined conventionally by the "right hand rule") and whose magnitude is equal to the product of the magnitudes of a and b times the sine of the angle between them. Since the dot product yields a scalar, it is often called the "scalar product". Likewise the cross product is often called the "vector product".

The dot product of ∇ and a vector field v(x,y,z) = v_x(x,y,z)i + v_y(x,y,z)j + v_z(x,y,z)k gives a scalar, known as the divergence of v, for each point in space:

The cross product of ∇ and a vector field v(x,y,z) gives a vector, known as the curl of v, for each point in space:

Notice that the gradient of a scalar field is a vector field, the divergence of a vector field is a scalar field, and the curl of a vector field is a vector field. Can we construct from the del operator a natural differential operator that creates a scalar field from a scalar field? Actually we already have the ingredients for such an operator, because if we apply the gradient operator to a scalar field to give a vector field, and then apply the divergence operator to this result, we get a scalar field. This is sometimes called the "div grad" of a scalar field, and is given by

For convenience we usually denote this operator by the symbol ∇², and it is usually called the Laplacian operator, because Laplace studied physical applications of scalar fields φ(x,y,z) (such as the potential of an inverse-square force law) that satisfy the equation , i.e.,

This formula arises not only in the context of potential fields (such as the electro-static potential in an electric field, and the velocity potential in a frictionless ideal fluid), it also appears in Poisson's equation  and in the fundamental wave equation

where c is the speed of propagation of the wave. Incidentally, this suggests another useful differential operator, formed by bringing the right hand term over to the left side to give

This operator is known as the d'Alembertian (because the wave equation was first studied by Jean d'Alembert), and it could be regarded as the dot product of two "dal" operators

where i,j,k,l are basis vectors of a four-dimensional Cartesian coordinate system.

One of the most important theorems in vector analysis is known as the Divergence Theorem, which is also sometimes called Gauss' Theorem. This is essentially just an application of the fundamental theorem of calculus

This enables us to express the integral of the quantity df/dx along an interval in terms of the values of f itself at the endpoints of that interval. Now suppose we are given a scalar function f(x,y,z) throughout a region V enclosed by a surface S, and we want to evaluate the integral of the quantity ∂f/∂x over this entire region. This can be written as

where the three integrals are evaluated over suitable ranges to cover the entire region V. For any fixed values of y = y₀ and z = z₀ the function f(x,y₀,z₀) is totally dependent on x, so we can evaluate the integral along any line parallel to the x axis through the region V for any particular y₀,z₀ using the fundamental theorem of calculus

where a,b are the x values at which the line intersects the surface S. (For ease of description we are assuming every line parallel to the x axis intersects the surface in only two points, but this restriction turns out to be unnecessary.) We now just need to integrate the above quantity over suitable ranges of y₀ and z₀ to give the integral throughout the entire region V. Notice that the two points (a,y₀,x₀) and (b,y₀,x₀) are both, by definition, on the surface S, at opposite ends of a line interval parallel to the x axis. Hence, we can cover all the contributions by integrating the value of the function f(x,y,z) over the entire surface S.

Of course, we recognize that f(a,y₀,z₀) is subtracted from the total, whereas f(b,y₀,z₀) is added, so it's clear that we need to apply a weighting factor to f(x,y,z) at each point when we integrate. The value for points on the "low" end of the intervals must be subtracted, and the value for points on the "high" end of the intervals must be added. Furthermore, if we want to evaluate the integration over the surface area of S by integrating over dS, we need to scale the magnitude of the contribution of each point to give the appropriate weight to each incremental region dS of the surface, because a portion of the surface that is very oblique to the yz plane doesn't "contribute as many line segments" parallel to the x axis as does an equal increment of the surface that is parallel to the yz plane.

Clearly the necessary scale factor at each point is the cosine of the angle between the positive x axis and the normal to the surface at that point. Notice that this automatically gives us the appropriate sign for each contribution as well, because (for a convex surface) the normal to the surface will have a positive x component on one end of the interval and a negative x component on the other, which means the cosines of the respective angles will have opposite signs. (Again, for ease of description we are assuming a convex surface, but it's not hard to show that this restriction is unnecessary, since a given line parallel to the x axis can have multiple segments which can be treated separately.)

Consequently, we can write our original integral as

where cos(n,i) denotes the cosine of the angle between a unit vector normal to the surface and a basis vector in the positive x direction. Naturally, since the coordinate axes are symmetrical, we could arrive at analogous results with x replaced by either y or z, and i replaced by j or k respectively.

Now suppose we are given a vector field F(x,y,z) with the components F_x(x,y,z), F_y(x,y,z), and F_z(x,y,z). Using the above results and simple additivity we have

The integrand on the left side is ∇·F, i.e. the divergence of F. Also, notice that cos(n,i), cos(n,j), and cos(n,k) are the components of the normal unit vector n, so the integrand on the right side is simply F·n, i.e., the dot product of F and the unit normal to the surface. Hence we can express the Divergence Theorem in its familiar form

Several interesting facts can be deduced from this theorem. For example, if we define F as the gradient of the scalar field φ(x,y,z) we can substitute ∇φ for F in the above formula to give

The integrand of the volume integral on the left is the Laplacian of φ, so if φ is harmonic (i.e., a solution of Laplace's equation) the left side vanishes. The integrand of the right hand integral is the normal "flux" through the surface, so we see that the integral of the normal flux over any closed surface (in a region that everywhere satisfies Laplace's equation) is zero. It follows that there can be no local maximum or minimum inside a region where Laplace's equation is satisfied, because such a point would, by definition, be completely enclosed by a surface of everywhere positive (or everywhere negative) normal flux, making it impossible for the integral of the flux over the surface to vanish. This, in turn, implies that if φ is constant over an entire closed surface (where Laplace's equations is satisfied) then the value of φ is constant throughout the enclosed volume, because otherwise the volume would have to contain a local maximum or minimum. Combining these facts with the additivity of harmonic functions, we can conclude that there is a unique harmonic function within an enclosed region that has specified values on the enclosing surface, because if φ₁ and φ₂ are two functions satisfying those boundary conditions, the harmonic field φ₁ – φ₂ is zero over the entire boundary, and therefore it vanishes throughout the interior as well.

If we allow non-zero charge or mass density (or sources or sinks) in the enclosed region, such that Poisson's equation ∇²φ = –4πr is satisfied, then the left hand integral is the net charge contained within the volume, and this equals the integral of the normal flux over the enclosing surface. This is often called Gauss' law of electrostatics, and it constitutes one of Maxwell's equations.

Another important consequence of the Divergence Theorem can be seen by noting that the scalar quantity ∇φ·n at any given point on the surface equals the partial derivative ∂φ/∂n where n is the displacement parameter in the direction normal to the surface. Furthermore, if the surface in question is a sphere – which we can assume without loss of generality is centered at the origin – then the normal displacement parameter n is equal to the radial parameter r. So for such a spherical surface we have

Recall that, in terms of spherical coordinates r, θ, and ϕ, where θ is latitude (zero at the North Pole) and ϕ is longitude (zero on the positive x axis) the basic line element in space is

so an incremental change dθ at constant r and ϕ corresponds to a change ds = r dθ, whereas an incremental change dϕ at constant r and θ gives ds = r sin(θ) dϕ. Hence the surface element in terms of θ and ϕ is dS = r² sin(θ) dθ dϕ , so the preceding integral can be written as

Applying Leibniz's Rule for the derivative of an integral, and multiplying by 4π/4π, this becomes

The quantity in the square brackets is just the mean value of φ(r,θ,ϕ) on the surface of the sphere, and this equation shows that the derivative of the mean value with respect to the radius r vanishes, so the mean value of φ on the surface of a sphere centered at any fixed point is independent of the radius. Considering the limit as r approaches zero, it's clear that the mean value of a harmonic function φ on the surface of a sphere (of any radius) is equal to the value of φ at the center of the sphere.

Return to MathPages Main Menu