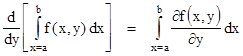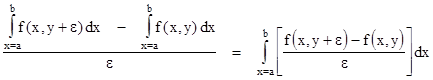|
Leibniz's Rule |
|
|
|
If f(x,y) is a well-behaved bi-variate function within the rectangle a<x<b, c<y<d, then we have |
|
|
|
|
|
This useful formula, known as Leibniz's Rule, is essentially just an application of the fundamental theorem of calculus. To prove this rule, we can simply expand the differentiations on both sides as follows |
|
|
|
|
|
|
|
in the limit as the real number ε approaches zero. Multiplying through by ε and distributing the integration on the right hand side, we see immediately that the equality holds. |
|
|
|
In a sense, Leibniz's Rule just expresses the fact that integration and differentiation are, in a sense, commutative. This can be seen more clearly if we define the operators (for any fixed constants a,b) |
|
|
|
|
|
Leibniz's Rule asserts the commutativity of these operators, i.e., we have |
|
|
|
DyIx = IxDy |
|
|
|
For an example of how this rule is used, see Differential Operators and the Divergence Theorem. |
|
|