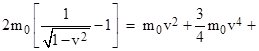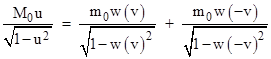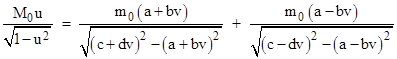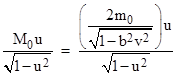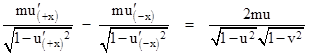Does Relativistic Mass Imply Special Relativity?

In a collection of essays on the subject of special relativity (“Six Not-So-Easy Pieces”), Richard Feynman presents the formula for relativistic mass

and then remarks that

For those who want to learn just enough about it so they can solve problems, that is all there is to the [special] theory of relativity – it just changes Newton’s laws by introducing a correction factor to the mass.

Unfortunately he gives no explicit explanation of this assertion. Later he discusses how the relativistic mass formula can be derived from the Lorentz transformation, but that’s the reverse of what’s needed to support the above claim, i.e., he needs to show that the Lorentz transformation follows from the relativistic mass formula. Incidentally, Feynman was well aware of the questionable nature of such claims. For example, in Vol II of his Lectures on Physics (section 26) he wrote

Whenever you see a sweeping statement that a tremendous amount can come from a small number of assumptions, you always find that it is false. There are usually a large number of implied assumptions that are far from obvious if you think about them sufficiently carefully.

Nevertheless, he did claim that all of special relativity follows from (1), so it’s interesting to consider in what sense this claim is valid. Some authors – especially those who disapprove of the notion of “relativistic mass” – have argued that Feynman was simply wrong, i.e., they assert that special relativity does not follow from relativistic mass.

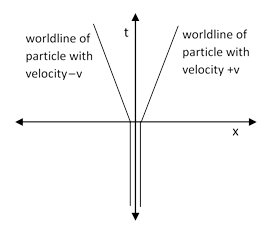
To examine this question, let’s consider two identical neutral particles, each of mass m₀, initially sitting side-by-side, at rest at the spatial origin of an inertial coordinate system S. Since the particles have v = 0, the combined mass of the two particles is presumably just 2m₀, and their total momentum is zero. Now suppose that at the time t = 0 these two particle somehow push against each other, and begin moving away from the origin in opposite directions at the speed v, as indicated in the spacetime diagram below.

The total momentum is still zero, but according to (1) the total relativistic mass of the two particles is now (choosing units so that c = 1)

At this point, from the standpoint of classical Newtonian mechanics augmented by the relativistic mass formula, we are faced with an apparent violation of the conservation of “mass”, because the relativistic mass has increased due to the acquired speed v of the particles. The apparent increase in relativistic mass of the particles is

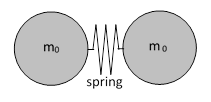
Of course, based on what we’ve said so far, we also have a violation of the conservation of energy, because initial the two particles were are rest (zero kinetic energy), and then they acquired the speed v, and we gave no indication of the source of this energy. One possibility is that there is a massless spring compressed between the two particles, which are held together (initially) by a latch, as illustrated below.

When the latch is released at time t = 0, the spring drives the particles apart. Thus the original and final configurations have the same energy, initially stored as potential energy in the compressed spring, and later in the form of kinetic energy of the particles. According to Newtonian mechanics (augmented with relativistic mass) the final kinetic energy of the two particles is

Thus to the second order the kinetic energy imparted to the particles equals the increase in the relativistic mass of the particles. It isn’t hard to show that the energy originally contained in the compressed massless spring must contribute actual rest mass to the original configuration. In other words, the total rest mass of the two particles latched together with the compressed massless spring between them must be greater than 2m₀.

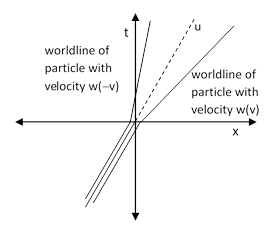
To show this, consider the same two particles, but this time the latched pair originally has a speed u in the positive x direction, and then at time t = 0 the latch is released, as indicated in the spacetime diagram below.

Now, a system of inertial coordinates for which the particles were originally at rest will be defined such that the two particles acquire the speed v is opposite directions when the latch is released. However, with respect to the original system of inertial coordinates, it’s clear that the speeds cannot equal simply u+v and u–v. We can say only that the final speeds (for any given u) will be w(v) and w(–v) for some function w, which we know must be linear fractional because these are the only entire meromorphic bijections. Thus for any given u we have

where a,b,c,d are functions of u. For conservation of relativistic momentum with respect to the original coordinates, we must have

where M₀ is the total rest mass of the initial configuration of the two particles plus the massless compressed spring between them (with energy to propel the particles to the speed v when unlatched). Inserting the linear fractional form of w into this equation and simplifying, we get

Without loss of generality we can set c = 1 (since we can divide through the linear fractional transformation by c). Also, in the case v = 0 we have M₀ = 2m₀ and the above equation reduces to

so we must have a(u) = u.  Furthermore, we note that the denominators on the right side are equal to each other if and only if ab = cd, so if we set ub = d the full equation becomes

We know that b(u) equals or approaches 1 as u goes to zero, so evidently the rest mass M₀ of the two particles plus the energy capable of propelling them to the speed v is not 2m₀ but rather

Thus conservation of momentum requires that the rest mass of the original configuration consist not just of the rest masses of the two particles, but also a contribution equal to the energy necessary to propel them apart at the speed v. We suggested an ideal massless spring to represent this energy, but the above argument applies to any form of energy (e.g., a small amount of gunpowder, accounting for the chemical energy). Hence we are forced to conclude that energy itself has inertia, and bound energy contributes to the rest mass of an object. It follows that relativistic mass is simply a measure of the energy of a system, so the conservation of energy is equivalent to the conservation of relativistic mass. Furthermore, for consistency with the relativistic mass formula (1) and the conservation of momentum, we must have a = d = u and b = c = 1, so the speeds (with respect to the original coordinates) of the two particles when unlatched must be given by

whereas the speeds of those particles with respect to the inertial coordinate system in terms of which the original configuration was at rest are simply +v and –v by the definition of inertial coordinates. This expression for composition of velocities leads, in turn, to the Lorentz transformation as the relationship between relatively moving systems of inertial coordinates

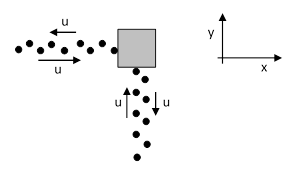
which are the only linear transformations consistent with the relativistic velocity composition formulas. Having established this, we can also determine the transformation of forces. In the relativistic context we can define “force” in different ways, since the various definitions that are equivalent to each other in Newtonian physics are distinct in relativistic physics. The most meaningful definition of force is the time derivative of momentum, where momentum is taken to be the product of relativistic mass and velocity. On this basis, we may ask how the components of a given force transform from one system of inertial coordinates to another. To answer this question, consider an object resting with respect to a certain inertial coordinate system, and suppose the object is being struck once per second by a sequence of perfectly elastic particles, each with rest mass m, moving with speed u in the positive x direction, and by another sequence of particles in the positive y direction. Each particle strikes the object and rebounds with equal speed in the opposite direction, as depicted below.

The force exerted by these particles is equal to the change in momentum per unit time. Each second a particle with rest mass m moving with speed +u rebounds with speed –u, so the net change of momentum per unit time gives the forces in the x and y directions

Now we consider the same situation in terms of a spatially aligned inertial coordinate system moving in the negative x direction with speed v. In terms of this system the object is moving to the right with speed v, and the incoming and rebounding particles in the x direction have speeds

Consequently, the net momentum contributed by each collision is

One such collision takes place each second in terms of the rest frame coordinates of the object, but since the object is moving with speed v relative to our new coordinates, we know from the Lorentz transformation that the collisions take place only once per (1–v²)^1/2 seconds, and therefore the rate of momentum transfer (and hence the force) in the x direction relative to the new coordinate system is

Thus the force parallel to the direction of motion is unchanged by the transformation to the new coordinates. Next we consider the force in the y direction, i.e., perpendicular to the direction of motion.  In this case the speeds of the incident and rebounding particles in the y direction are given by

which we infer from the fact that the transverse distances they travel are unchanged so their speeds are reduced by the time dilation factor. In addition, the incident and rebounding particles also have a transverse speed v in the x direction. Therefore, the total squared speed of the particles (both incident and rebounding) is

Using this we can compute the net transferred momentum per collision is

Again, one such collision takes place each second in terms of the rest frame coordinates of the object, and since the object is moving with speed v relative to our new coordinates, the collisions take place only once per (1–v²)^1/2 seconds in terms of the new coordinates, so the rate of momentum transfer (and hence the force) in the y direction relative to the new coordinate system is

Thus the force perpendicular to the direction of motion is reduced by the factor (1–v²)^1/2 in terms of the new coordinates. It’s worth noting that this transformation of forces, based entirely on mechanical considerations, agree with how the electromagnetic force transforms under Lorentz transformations, as discussed in the note on Force Laws and Maxwell’s Equations.

In summary, we’ve shown that the relativistic mass formula (1), combined with conservation of momentum in the Newtonian context, does indeed imply special relativity, at least to the extent of implying the equivalence of mass and energy, and the Lorentz transformation relating relatively moving systems of inertial coordinates. It might be argued that we have considered only mechanical systems, and can’t conclude anything about (for example) the propagation of light from equation (1). However, we’ve seen that (1) implies all forms of energy have inertia. For example, we could imagine a pulse of light bouncing between the mirrored surfaces of the two particles when latched together, and we would find that the energy of that pulse of light contributes to the rest mass of the bound configuration, just as did the energy of a compressed spring. Hence a pulse of light is an inertial entity, and must satisfy conservation of momentum, so it too must propagate in conformity with equation (1), which of course involves the constant c, defined as the speed of light. Hence we have tacitly introduced electromagnetism into the relativistic mass formula.

The usefulness (and even the validity) of the concept of “relativistic mass”, as distinct from “rest mass”, has often been debated, but it seems to be overlooked by both sides that at least some (and perhaps all) of the rest mass of typical physical entities ultimately consists of relativistic mass. For example, the “rest mass” of a billiard ball at a given temperature consists partly of the relativistic mass of the molecules comprising the ball, since those molecules are in motion even while the ball is stationary. Also the binding energy of molecules, and various other forms of potential energy, contribute to the rest mass, so the idealized image of “rest mass” as a primitive attribute of some localizable entity seems fundamentally misguided. The idea of invariant rest mass is perhaps best adapted to the study of sub-atomic particles, since those entities come closest to being irreducible, and hence the assignment of a primitive invariant rest mass to such entities often seems justified. However, even in this context we know an electron and a positron can annihilate each other, giving off electromagnetic energy, leaving no “matter” at all. Of course, it remains possible to define the “rest mass” of the total emitted electro-magnetic energy, but in so doing we are identifying a rest mass for the combination of multiple entities (photons), each of which has zero rest mass. If effect, this rest mass consists entirely of relativistic mass. (See The Inertia of Energy for more on this topic.)

Return to MathPages Main Menu