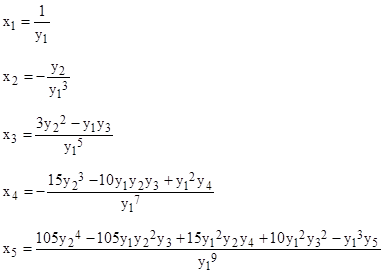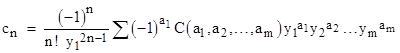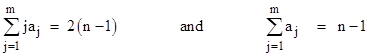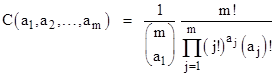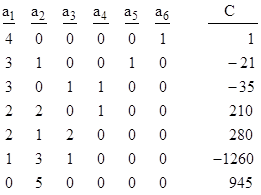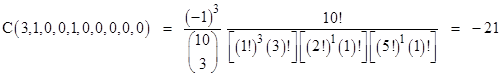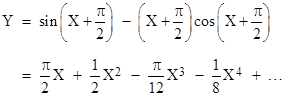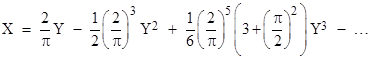Inverse Functions

As discussed in the note on grazing goats, a differentiable function y(x) can be inverted at any given point x₀, y₀ to give a power series for the function x(y). Writing this power series as

it’s clear that the coefficients c_n are related to the derivatives of x with respect to y by

Hence in order to determine the coefficients of the power series of this inverted function we need only determine the derivatives of x with respect to y. Our task is to determine these derivatives from the known derivatives of y with respect to x. We have y₀ = y(x₀). Letting positive integer subscripts on either of these variables denote derivatives with respect to the other variable, we saw in the previous note that the derivatives are related by

Using this formula we can determine the expressions

and so on. For a simple example, suppose we wish to determine the power series for the inverse of the exponential function y = e^x. In this case y_n = e^x for all n, and substitution into the preceding expressions gives

and so on. We choose to expand the series about the point x₀ = 0, y₀ = 1, so we evaluate these derivatives at x₀ = 0, and we find that

Substituting these expressions into the equations for the coefficients, we get the series

which of course is the power series for the natural log, the inverse of the exponential function.

Notice that the numerators of the expression for x_n contains a term for each partition of m = 2(n–1) into exactly (n–1) parts.  Also, the overall signs alternate for successive n, so we can write the general coefficient of the inverse function in the form

where the summation is evaluated over all sets of non-negative integers a₁, a₂, …, a_n such that

The “C” coefficients in the preceding expression are related to the multinomial and binomial coefficients. Specifically, we have

To illustrate, we will use these formulas to determine the general expression for the 6th order coefficient in the power series of the inverse function. The seven partitions of m = 2(n–1) = 10 into exactly (n–1) = 5 parts are listed below, along with the corresponding C coefficients.

To illustrate how the coefficients are computed, the coefficient corresponding to the second of these partitions is

Notice that the sum of the coefficients for n = 6 is (n–1)! = 120, as required. From these results we can now write the sixth order coefficient in the power series expansion of the general inverse function:

Naturally these results are consistent with the “reversion of series” formulas, which apply in cases when the original function is given as a power series and we wish to find the power series of the inverse function. We can always shift the variables so that we are expanding about the point x₀ = y₀ = 0, and as always we require that the derivative of y(x) be non-zero, so we are given a series of the form

and we wish to determine the coefficients of the reverted series

Inserting the values of the derivatives y₁ = h₁, y₂ = 2h₂, y₃ = 6h₃, etc., into the previous formulas, we get

and so on.  In these terms the coefficients in the numerators sum to unity. In the note on grazing goats we considered the function y = sin(x) – x cos(x) at the point x₀ = π/2, y₀ = 1, so we could just as well have proceeded by re-writing the function in terms of the re-scaled parameters X = x – π/2 and Y = y – 1, which gives

Then application of the preceding formula for series reversion gives

in agreement with the result found by evaluating the derivatives.

It’s interesting that the condition that must be met by a function y(x) in order for the third derivative of x(y) to vanish is y₁y₃ – (1/3)y₂² = 0 which, if we set s₀ = y₁ and differentiate again, gives

This is of the same general form as the ubiquitous “separation equation” in physics. (See the note on inertial and gravitational separations.) This is also reminiscent of the question about whether an accelerating charge radiates, a question that hinges on whether radiation is associated with the second or the third derivative of position with respect to time.

Return to MathPages Main Menu