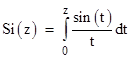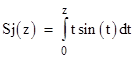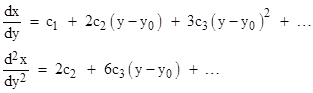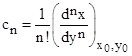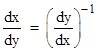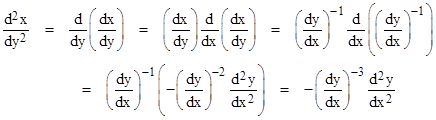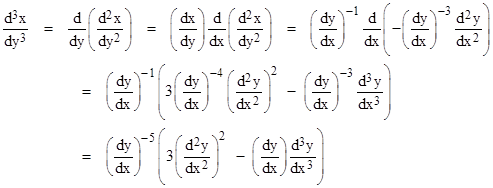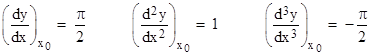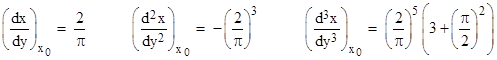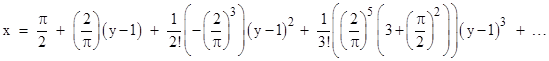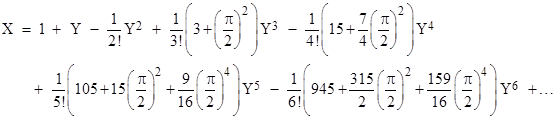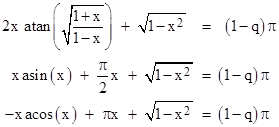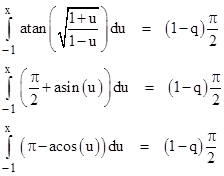The Mystery of the Grazing Goat

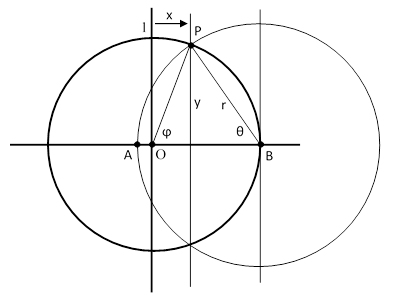
The University of Maryland's European Division conducts classes at the undergraduate level on US military bases all over Europe, and one of the math problems featured in their course work is the old question about a goat grazing in a circular pasture. The statement of the problem goes like this: Consider a fenced circular pasture with known radius. At the edge of this pasture is a pole with a rope attached to it. At the other end of the rope we attach a goat. What length of rope is required if we want the goat to graze over exactly half the area of the pasture? The situation is as shown in the figure below.

The pasture is represented by the circle of radius 1 through B centered at O, and the rope is attached to the fence at point B. The limit of the goat’s tether is the circle of radius r through P centered at B. The upper half of the region reachable by the goat consists of a slice of the circle of radius r subtended by the angle θ, plus a slice of a unit circle subtended by the angle ϕ, minus the triangular region OPB.  We wish to set the area of this region equal to some specified fraction q (such as one half) of the area of the upper half of the pasture (i.e., the upper half of the unit circle). Thus we have

Multiplying through by 2 and simplifying, we get

Since PB is an arc of the circle centered at O, the angle OPB equals the angle OBP, and so θ = (π–ϕ)/2. Also, from the relations r² = (1–x)² + y² and y² = 1 – x², we have r² = 2(1–x). Using these facts, the above equation can be written in the form

Re-arranging terms and making the substitutions x = cos(ϕ) and y = sin(ϕ) gives

Furthermore, if we set α = π – ϕ, and note that sin(π–ϕ) = sin(ϕ) and cos(π–ϕ) = –cos(ϕ), this equation can be written as

Given any fraction q (the fraction of the circular pasture reachable by the goat), we can solve this equation for the angle α, and then the length of the rope is given by

For example, the usual problem statement calls for q = 1/2 (i.e., the goat can reach half of the pasture), and with this value of q equation (1) implies that α = 1.9056957…, and so the length of the rope is r = 1.15872847301… times the radius of the pasture.

Despite the simplicity of this problem, it seems to exert a strong fascination on some people, apparently due to the fact that equation (1) gives the value of α only implicitly, rather than as some explicit expression of the form α = f(q) for some “known” function f. It’s really quite remarkable how this problem appeals to people’s imagination, as if there was something profound and/or mysterious about the fact that the length of the rope is not expressible in “closed form”. It takes on a significance in the minds of some people that is difficult to understand. (One man said his father had asked him for an “analytical solution” of the grazing goat problem ten years before he died, and he – the son – had been seeking the solution ever since…) This may be partly a result of the usual education process, in which children are exposed almost exclusively to problems whose solutions have tidy expressions in terms of a small set of elementary functions. This tends to produce the (false) impression that most problems have such solutions. The reaction of people when they first encounter a problem like the grazing goat is reminiscent of the shock of the ancient Greek mathematicians when they first realized that not all numbers are rational, the circle cannot be squared and not all angles can be trisected (by straightedge and compass), and so on. At first people tend to regard such things as bizarre exceptions and anomalies, but gradually they realize that these “intractable” problems are the rule rather than the exception.

The fixation on “closed form” solutions among people who are not too familiar with mathematics is also based partly on the naïve view of “standard functions”, and of the difference between implicit and explicit conditions. For example, they might accept “the square root of two” as an explicit answer, even though these words are just a verbal way of expressing the implicit condition x² – 2 = 0. Likewise an answer like “π/2” is based on the definition of the transcendental number π, which is not even the root of any algebraic equation. As for “standard functions”, it’s questionable whether that term has any objective meaning. Consider, for example, the sine integral function

Just as with the usual trigonometric functions, we can represent this as a power series, and its values are tabulated in many reference books, so it may be regarded as a standard function. We can also define the inverse of this function, i.e., we can let z = invSi(u) denote the value of z such that Si(z) = u. But the decision to define these as “standard functions” is subjective. We could just as well define a function such as

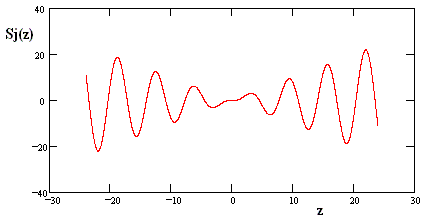
A plot of this function is shown below.

Notice that Sj(z) = sin(z) – z cos(z), so the solution of the grazing goat problem can be expressed in “closed form” using the inverse of this function (made unique by specifying it as the smallest positive value), i.e.,

This illustrates the fact that whether or not a number can be expressed in “closed form” is largely conventional, since it depends on what functions we choose as our “standard functions”. There is no absolute objective reason that Si should be considered such a function while Sj should not. Also, by allowing inverse functions, we can always just take an implicit condition defining a number, and invert it to give the desired number “explicitly”.

Another source of confusion is the term “analytic”. People ask for an analytic solution, but this can be confused with the concept of an analytic function, which is a function that has complex derivatives and a power series representation (in the region of interest). In this sense there actually is an “analytic solution” to the goat grazing problem, i.e., the length of the rope can be expressed as a power series in the fraction q. This follows from the existence of derivatives of the implicit function. In general, given an explicit differentiable function y(x), we can determine a power series for the inverse function x(y) at any desired point (x₀,y₀) where dy/dx is not zero by evaluating the derivatives of x with respect to y at that point. (The symbols “x” and “y” here refer to generic variables, not to be confused with the coordinates in the pasture discussed previously.) The desired power series is of the form

which has the derivatives

and so on. Hence we can evaluate the coefficients in terms of the derivatives at the point (x₀,y₀). Specifically, we have

We immediately have c₀ = x₀ = x(y₀), and our task is to deduce the derivatives of x with respect to y from the derivatives of y with respect to x. The first derivative is found directly by taking the reciprocal, i.e.,

Then the second derivative is given by

From this we can determine the third derivative as

and so on for successively higher derivatives. As an example, consider the goat-grazing function

and let us expand the inverse function x(y) about the point y₀ = 1, which corresponds to the value x₀ = π/2. The derivatives of y with respect to x are

so at the point x₀ we have

Inserting these values into the previous expressions, we get the derivatives of x with respect to y at this point

Thus the power series for x as a function of y is

In terms of the re-scaled parameters X = (2/π)x and Y = (2/π)(y–1) this can be written (including a few additional terms) as

The original grazing goat problem has q = 1/2 and hence y = π/2. Evaluating the series up to the Y⁸ term leads to the rope length r = 1.158796… as opposed to the exact value of 1.158742…  The series is convergent on the exact value in this region, so the exact solution is an analytic function of q. Of course, this is not what most people have in mind when they ask if there is an “exact analytic solution”.

Incidentally, the solution can also be expressed in several other forms. For example, the x coordinate of the point P discussed previously must satisfy each of the equations

The left sides of each of these equations have very simple derivatives, leading to the equivalent conditions in terms of integrals

I was talking once with a young woman who had never before (and has never since) expressed any interest in mathematics, but when she heard about this math web site she immediately took me aside and said "Please tell me this:  Suppose you have a goat penned up in a circular pasture..." She was seriously intent on learning the answer to that question, which I thought was rather odd. Later I learned that her husband was in the military, and they had been stationed in Europe for several years, so I wonder if we have the University of Maryland to thank for their interest in that problem.

The standard goat grazing problem with q = 1/2 is just one of a general class of area problems involving shapes whose boundaries are segments of circles.  Such shapes are called "lunes". Suppose that, instead of leaving half of the pasture untouched, we want to leave 1/π untouched. In this case the length of the rope must be the square root of 2 (times the radius of the pasture). Of course, this is just the same as saying that r is the root of r² – 2 = 0, and whether this is considered a "closed form" solution depends on your point of view, since we can compute the actual value of square root of 2 only by iterative procedures. On the other hand, it can be constructed by Euclidean methods, i.e., by straightedge and compass, so this type of solution can claim to possess a very elementary type of "constructability".

Return to MathPages Main Menu