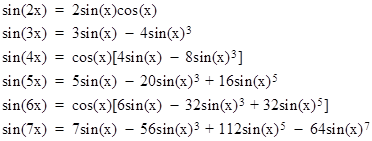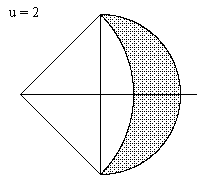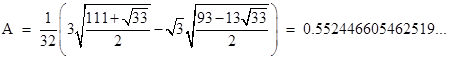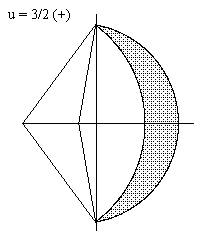The Five Squarable Lunes

A planar region whose boundaries are arcs of two circles is called a lune (presumably because it resembles a crescent moon). Of course, it's impossible to "square” a complete circle by Euclidean methods – meaning that we can’t construct a square with the same area using just straightedge and compass – but, somewhat surprisingly, it is possible to “square” certain lunes. Hippocrates of Chios was the first to demonstrate such quadratures of lunes around 440 BC. It turns out that only five particular lunes can be squared by Euclidean methods. Three of these were described by Hippocrates himself, and two more were discovered in the mid 1700's. These last two are often credited to Euler in 1771, but according to Heath all five squarable lunes were given in a dissertation by Martin Johan Wallenius in 1766. The proof that these five are the only lunes squarable by Euclidean methods was given by Tchebatorew and Dorodnow.

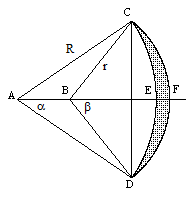
It's not too difficult to discover these five squarable lunes, especially with the help of modern trigonometric methods. In general, consider the lune described by arc segments of two offset circles, one of radius r and the other of radius R, as shown below.

Under what conditions can we solve for the area of the lune (the shaded region) by Euclidean methods? This is equivalent to asked for the conditions in which we can solve for the shaded area by means of nothing more complex than quadratic equations and square roots. The area of the lune can be expressed as the difference between the two part-circular regions to the right of the vertical line, i.e., we have

We can express the area of the region CFD as follows

Now, since the area of a complete circle of radius r is πr², the area of the circular sector BCFD is simply

Also, the area of the triangle BCD is

where we have used the trigonometric identity 2sin(x)cos(x) = sin(2x). Therefore, the area of the region CFD is

Similarly we have

Hippocrates saw that we could eliminate the transcendental terms βr² and αR² from the expression for the area of the lune if we set those terms equal to each other. Thus, we restrict ourselves to only those cases where βr² = αR². In these cases the area of the lune is simply

Now, since we want to be able to construct this area from a unit length (such as taking r = 1) using only quadratic operations, the length of R must be constructible, so we will require it to be of the form R² = ur² so that R equals r times the square root of some rational number u. It follows from the relation βr² = αR² that β = uα, so we can make these substitutions into the expression for the lune area to give

Of course, from the original diagram we can equate the vertical heights to give the relation r sin(β) = R sin(α), which implies

Recalling the identities sin(2x) = 2sin(x)cos(x) and cos(x)² = 1 - sin(x)² we can rewrite the equation for the area of the lune entirely in terms of sin(α), which we will abbreviate as s.

Therefore, we can "square the lune" (with apologies to Debussey) by Euclidean methods if we can determine s = sin(α) by solving nothing more complicated than quadratics. Clearly equation (1) can be solved for sin(α) by means of quadratics and square roots only for certain values of the rational number u. To see this, recall the well-known trigonometric identities for multiple angles

and so on. If we set u = 2 in equation (1), and again denote sin(α) as simply s, we have

and so s² = 1/2 and . Substituting this into (2), and setting r = 1, we get the area A = 1. This was the first case found by Hippocrates, and is shown below.

Notice that the area of the lune equals the area of the major triangle to the left of the vertical line.

Now consider what happens if we set u = 3. In this case equation (1) becomes

and so we have

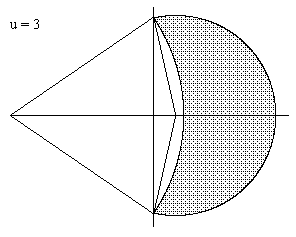
Substituting into equation (2) gives the area of the lune

This lune is shown in the figure below.

For the third squarable lune, consider what happens if we set u = 3/2. In this case we can define the half-angle ω = α/2 so we have α = 2ω and uα = 3ω. Equation (1) then becomes

We can now use the trigonometric multiple angle formulas to expand this into an equation in terms of S = sin(ω) as follows

Squaring both sides and simplifying gives a quadratic in S²

which gives

(The other root leads to a complex result.) This is sin(ω)², which equals sin(2α)², so we need to convert this to an expression for sin(α) using the half-angle formula, which gives

and so we have the angle α = 0.935929456...  On this basis the area of the lune is

This lune is illustrated below.

Apparently the above three cases were the only ones known in antiquity. The next case for which equation (1) reduces to a quadratic is with u = 5, which leads to

where s again denotes sin(α). Solving this for s² gives

The root with the "+" sign leads to a complex angle, but with the "–" sign we get α = 0.409090011..., which produces the squarable lune shown below.

The only other value of u for which equation (1) reduces to a quadratic equation is u = 5/3. In this case we write the equation in terms of ω = α/3, so letting S denote sin(ω) we have

This is a quadratic in S², so we can solve it to give

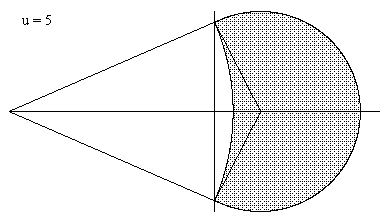
Taking 3 times the inverse sine of the square root of these quantities gives the two possible values of the angle, of which only the first is relevant, so we have the angle

This last squarable lune is illustrated below.

Return to MathPages Main Menu