|
Hawking Radiation as Delayed Choice |
|
|
|
According to classical general relativity, mass-energy cannot depart from the interior of a black hole, because nothing can cross an event horizon “in reverse”. The event horizon is the surface at which the forward light cones are tilted inward to the extent that they are entirely contained inside the surface. Therefore, the passage of any mass-energy from inside to outside the event horizon would require (according to classical general relativity) superluminal propagation, and hence it is ruled out, and as a consequence the mass-energy content of a black hole can never decrease. However, applying quantum mechanical concepts, Hawking described a process by which a quiescent black hole would radiate, so the mass-energy content would decrease over time. The predicted rate of this radiation for stellar-sized black holes is extremely small, but the prediction of any outward radiation at all from an event horizon – no matter how weak – is remarkable, since it appears to conflict with one of the foundational principles of general relativity, namely, the principle of no super-luminal propagation of mass-energy. |
|
|
|
Several different explanations of Hawking radiation can be found in popular descriptions. A few of these explanations are summarized below. |
|
|
|
(1) Quantum fluctuations lead to the production of pairs of particles and anti-particles just outside the horizon; one of these falls into the black hole and the other escapes as radiation with positive mass-energy. The in-falling particle has negative mass-energy, so its absorption results in a reduction in the mass-energy of the black hole. |
|
|
|
(2) The same as (1), except that both particles have positive mass-energy (recognizing that anti-particles don’t have negative mass-energy). The reduction in the mass-energy of the black hole is attributed to the expenditure of work by tidal forces to separate the two particles. This work exceeds the mass-energy of the absorbed particle by an amount equal to the mass-energy of the radiated particle. |
|
|
|
(3) Fluctuations occurring just inside the horizon of a black hole produce pairs of particles, and one particle of such a pair may “tunnel” out through the event horizon (exploiting the phenomenon of quantum tunneling), becoming external radiation, leaving the other inside with negative energy, diminishing the mass-energy of the black hole. |
|
|
|
(4) Quantum vacuum fluctuations can be analyzed into positive and negative frequencies. If the propagating fluctuations in the far future (far from the black hole) are extrapolated back into the far past (prior to the formation of the black hole), it is found that the future positive-frequency fluctuations are consistent with the emission of radiation from the black hole and the absorption of negative frequency components by the black hole, diminishing its mass-energy. |
|
|
|
The fourth explanation seems to be the closest to the actual derivation, and it’s worth noting that it explicitly relies on an analysis beginning prior to the formation of the black hole. Thus it would not apply (at least not in any obvious way) to a black hole that has always existed. It might be argued that such an object is not possible, since the universe itself seems to have a definite beginning in the finite past, but even in this context we might imagine primordial black holes, i.e., gravitationally collapsed regions which have existed from the very beginning of the universe. It’s unclear (to me) how the Hawking analysis (4) could be applied to such an object, because there would be no time prior to the formation of the black hole. |
|
|
|
It’s interesting to compare this with the question of whether a uniformly accelerating charged particle radiates. According to the Lorentz-Dirac equations of classical electrodynamics, the answer seems to be no, but this applies only to a particle that has always been uniformly accelerating (and that will always continue to accelerate uniformly), which is presumably not a realistic condition. For any realistic particle, there must have been a time prior to when the particle began its uniform acceleration, and this change in acceleration results in radiation, in a sense because the Fourier transform of the particle’s motion acquires impurities from the change in acceleration. This is analogous to the fact that a purely monotonic signal must be eternal, because any beginning or ending introduces other frequency components to the function for the entire signal. |
|
|
|
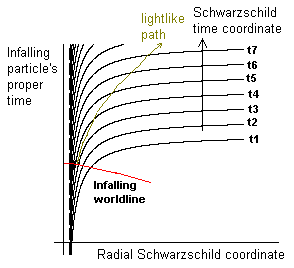
In the context of general relativity it isn’t too difficult to arrive at an interpretation of Hawking radiation that is consistent with these ideas. As discussed in another note, the worldline of every particle that falls into a black hole continues to have a lightlike (null) connection to all external distances at all future times. This is illustrated in the qualitative spacetime diagram below. |
|
|
|
|
|
|
|
The red curve signifies the worldline of an in-falling particle, and the gold curve represents a lightlike (null) locus from the in-falling particle to the exterior region in the future. The important point is that the in-falling worldline passes through every one of the external Schwarzschild times (to future infinity) prior to actually crossing the event horizon. As it passes through each of these times, there still null paths from the particle to the future exterior, so the in-falling particle has (in a sense) infinite opportunities to radiate to the exterior region, out to arbitrarily late times, even though we would normally consider the particle to have passed inside the event horizon by approximately the Schwarzschild time denoted by t1 on the figure. According to the causal structure of spacetime in classical general relativity, we can never (at any external time) conclude for certain that the particle has emitted its last photon prior to crossing the event horizon. |
|
|
|
In fact, carrying this further, we might ask if there is ever a time when we (in the external region) can conclude for certain that the particle itself is going to cross the event horizon. From the classical standpoint we might be able to compute a “point of no return”, but given the existence of quantum fluctuations it may not be straightforward to determine this point with absolute certainty. Also, the superposition of outcomes might be resolved only at later times, as in “delayed choice” EPR experiments involving quantum entanglement. As evaluated at some external time, the state of an in-falling particle in the past may be uncertain, or rather in a superposition of states, one falling through the event horizon without emitting any more radiation, and the other emitting some additional radiation or (perhaps) being ejected itself, and never falling through the horizon. The irreversible outcome may be determined only at some time in the distant future. In the mean time, the particle’s condition is analogous to that of Schrödinger’s cat, neither alive nor dead, but in a superposition of alive and dead. Every particle that has (presumptively) crossed an event horizon and contributes to the mass-energy of a black hole is arguably in this condition. If so, then a black hole itself is essentially a quantum mechanical apparition (or fluctuation), whose eventual “evaporation” is therefore less surprising. We could regard Hawking radiation as the very gradual completion of a series of delayed-choice experiments, eventually yielding the final irreversible result that nothing ever actually fell through the event horizon. |
|
|
|
The most obvious objection to this interpretation is that any radiation emitted from a particle very close to the event horizon will be extremely red-shifted to an external observer, and the intensity will drop exponentially with time for that observer. But this assumes the classical continuous model of radiation, propagating strictly along null intervals. In the context of quantum field theory a photon has a non-zero amplitude to be exchanged even along spacelike intervals. Such photons would be virtual with respect to the local free-falling coordinates at the point of emission, but may be real with respect to the stationary external coordinates. This is closely related to the usual description of Hawking radiation, except that it makes use of delayed-choice interactions with the in-falling particles comprising the black hole, rather than regarding the radiation as arising from vacuum field fluctuations. |
|
|
|
Whether or not this approach leads to a consistent account of Hawking radiation, it would not be surprising if there exists some description of Hawking radiation in terms of direct actions between particles. Any phenomena that can be described in terms of mediating fields can also be described in terms of direct actions between particles, dispensing with the fields entirely. For example, although electrodynamics is most commonly described in terms of Maxwell’s field theory, it can also be developed along the lines of Ampere and Weber as a distant-action theory with no fields at all. Of course, the opposite is also true, i.e., quantum field theory can be expressed entirely in terms of fields, without reference to particles. |
|
|