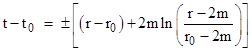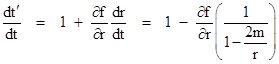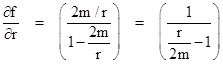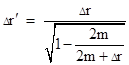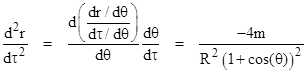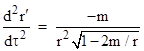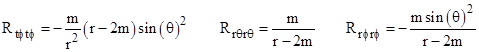7.3  Falling Into and Hovering Near A Black Hole

 

Unless the giddy heaven fall,

And earth some new convulsion tear,

And, us to join, the world should all

Be cramped into a planisphere.

As lines so loves oblique may well

Themselves in every angle greet;

But ours, so truly parallel,

Though infinite, can never meet.

Therefore the love which us doth bind,

But Fate so enviously debars,

Is the conjunction of the mind,

And opposition of the stars.

Andrew Marvell (1621-1678)

 

The empirical evidence for the existence of black holes – or at least something very much like them − has become impressive, although it is arguably still largely circumstantial. Indeed, most relativity experts, while expressing high confidence (bordering on certainty) in the existence of black holes, nevertheless concede that since any electromagnetic signal reaching us must necessarily have originated outside any putative black hole, it may always be possible to imagine that they were produced by some mechanism just short of a black hole. Hence we may never acquire, by electromagnetic signals, definitive proof of the existence of black holes – other than by falling into one. On the other hand, recent observations of gravitational waves matching the signature of two coalescing black holes have provided nearly conclusive evidence of actual black holes (in the local sense).

 

Of course, there are undoubtedly bodies in the universe whose densities and gravitational intensities are extremely great, but it wasn’t self-evident that general relativity would remain valid in these extreme conditions. Ironically, considering that black holes have become one of the signature predictions of general relativity, the theory’s creator published arguments purporting to show that gravitational collapse of an object to within its Schwarzschild radius could not occur in nature. In a paper published in 1939, Einstein argued that if we consider progressively smaller and smaller stationary systems of particles revolving around each other under their mutual gravitational attraction, the particles would need to be moving at the speed of light before reaching the critical density. Similarly Karl Schwarzschild had computed the behavior of a hypothetical stationary star of uniform density, and found that the pressure must go to infinity as the star shrank toward the critical radius. In both cases the obvious conclusion is that there cannot be any stationary configurations of matter above the critical density. Some scholars have misinterpreted Einstein’s point, claiming that he was arguing against the existence of black holes within the context of general relativity. These scholars underestimate both Einstein’s intelligence and his radicalism. He could not have failed to understand that sub-light particles (or finite pressure in Schwarzschild’s star) meant unstable collapse to a singular point of infinite density – at least if general relativity holds good. Indeed this was his point: general relativity must fail. Thus we are not surprised to find him writing in “The Meaning of Relativity”

 

For large densities of field and matter, the field equations and even the field variables which enter into them have no real significance. One may not therefore assume the validity of the equations for very high density of field and matter… The present relativistic theory of gravitation is based on a separation of the concepts of “gravitational field” and of “matter”. It may be plausible that the theory is for this reason inadequate for very high density of matter…

 

These reservations were not considered to be warranted by other scientists at the time, and even less so today, but perhaps they can serve to remind us not to be too dogmatic about the validity of our theories of physics, especially when extrapolated to very extreme conditions that have never been (and may never be) accessible to observation.

 

Furthermore, we should acknowledge that, even within the context of general relativity, the formal definition of a black hole may be impossible to satisfy. This is because, as discussed in the previous section, a black hole is usually defined as a region of spacetime that is not in the causal past of any point in the infinite future. Notice that this refers to the infinite future, because anything short of that could theoretically be circumvented by regions that are clearly not black holes. However, in some fairly plausible cosmological models the universe has no infinite future, because it re-collapses to a singularity in finite coordinate time. In such a universe (which could conceivably be our own), the boundary of any gravitationally collapsed region of spacetime would be contiguous with the boundary of the ultimate collapse, so it wouldn’t really be a separate black hole in the strict sense. As Wald says, "there appears to be no natural notion of a black hole in a closed Robertson-Walker universe which re-collapses to a final singularity", and further, "there seems to be no way to define a black hole in a closed universe, because it requires going to infinity, but there is no infinity in a closed universe."

 

It’s interesting that this is essentially the same objection that is often raised by people when they first hear about black holes, i.e., they reason that if it takes infinite coordinate time for any object to cross an event horizon, and if the universe is going to collapse in a finite coordinate time, then it’s clear that nothing can possess the properties of a true black hole in such a universe. Thus, in some fairly plausible cosmological models it's not strictly possible for a true black hole to exist. On the other hand, it would still be possible to have an approximate notion of a black hole in some isolated region of a closed universe.

 

Having said this, there’s nothing to prevent us from considering an infinite open universe containing full-fledged black holes. These ideal black holes involve singular boundaries at which the usual Schwarzschild coordinates for the external field of a gravitating body go to infinity − and back − as discussed in the previous section. There are actually two distinct kinds of "spacetime singularities" involved in an ideal black hole, one of which occurs at the center, r = 0, where the spacetime manifold actually does become unequivocally singular and the field equations are simply inapplicable. It's unclear (to say the least) what this singularity actually means from a physical standpoint, but oddly enough the "other" kind of singularity involved in a black hole seems to shield us from having to face the breakdown of the field equations. This is because it seems (although it has not been proved) to be a characteristic of all realistic spacetime singularities in general relativity that they are invariably enclosed within an event horizon, which is a peculiar kind of singularity that constitutes a one-way boundary between the interior and exterior of a black hole. This is certainly the case with the standard black hole geometries based on the Schwarzschild and Kerr solutions. The proposition that it is true for all singularities is sometimes called the Cosmic Censorship Conjecture. Whether or not this conjecture is true, it's a remarkable fact that at least some (if not all) of the singular solutions of Einstein's field equations automatically enclose the singularity inside an event horizon, an amazing natural contrivance that effectively shields the universe from direct two-way exposure to any regions in which the metric of spacetime breaks down.

 

Although we don’t know what to make of the true singularity at r = 0, the physics near the event horizon at r = 2m (for a non-rotating black hole) is somewhat more tractable. The Schwarzschild coordinates become singular at this location, as do the metric coefficients expressed in terms of those coordinates, but of course a singularity in a coordinate system doesn't necessarily represent a physical singularity of the manifold. (Consider traveling due East at the North Pole). Nevertheless, the coordinate singularity at r = 2m is not entirely inconsequential, because it does (or at least can) represent a unique globally significant boundary between fundamentally separate regions of spacetime, depending on the cosmology. To understand the nature of this “boundary”, we might try to examine the light cone structure near the event horizon, but we find that even the appearance of this structure can be misleading if we view it in terms of unsuitable coordinates. For example, as discussed Section 6.4, if we focus on just the radial and the time coordinates of the Schwarzschild metric (i.e., considering just intervals along a fixed angular direction), we have (dτ)2 = (1−2m/r)(dt)2 − (1−2m/r)−1(dr)2, and hence the trajectories of outward and inward pulses of light (dτ = 0) satisfy

 

 

Integrating these relations, the equations for light rays emanating from any event t0,r0 are

 

 

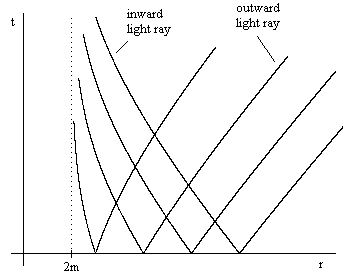
A plot depicting the inward and outward light rays emanating from four points near the event horizon of a black hole is shown below.

 

 

This image might seem to suggest that no light ray ever crosses the event horizon, but this is misleading, because of the singularity of the Schwarzschild time coordinate “t” at the horizon. The components of the curvature tensor at r = 2m are on the order of 1/m2, so the manifold itself is smooth at that location, and there ought to be a time coordinate in terms of which the inward rays of light cross over the event horizon smoothly. This leads us to seek a new time coordinate, which we will call tʹ, in terms of which dr/dtʹ = −1 for inward paths of light. Equation (1) gives dr/dt = −(1 − 2m/r) for these rays, so we want to define tʹ such that dtʹ/dt = (1 – 2m/r). If we define tʹ = t + f(r) for some function f, we have

 

 

so to give the desired result we must have

 

 

which implies that f(r) = 2m ln(r/2m − 1), and hence our new time coordinate is

 

 

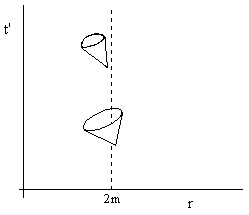
The coordinates tʹ,r are known as (inward) Eddington-Finkelstein coordinates. The inward light paths have a slope of −1, but the outward light paths have a slope of (1 − 2m/r)/(1 + 2m/r), so they are still “vertical” at the event horizon. The figure below depicts the future light cones of two events located on either side of a black hole's event horizon, in terms of inward Eddington-Finkelstein coordinates.

 

 

The right-hand ray of the cone for the event located just inside the event horizon is tilted just slightly to the left of vertical, whereas the cone for the event just outside 2m is tilted just slightly to the right of vertical. The rate at which this "tilt" changes with r corresponds to the curvature at this location, and for a sufficiently large black hole this rate can be made negligibly small. However, by making this rate small, we also make the outward ray more nearly "vertical" for a radial coordinate r that exceeds 2m by any given ratio greater than 1, which implies that the hovering observer's frame needs to be even more "boosted" relative to the local frame of an observer falling freely from infinity. The gravitational potential, which need not be changing very steeply at r = 2m, has nevertheless changed by a huge amount relative to infinity. We must be very deep in a potential hole in order for the light cones to be tilted that far, even though the rate at which the tilt has been increasing can be arbitrarily slow. This just means that for a super-massive black hole they started tilting at a great distance. In other words, for an observer "hovering" at a value of r that exceeds 2m by some arbitrarily small fixed ratio, the downward acceleration required to resist the inward pull can be arbitrarily small for sufficiently large m, but in order for the observer to be hovering close to 2m, his frame must be tremendously "boosted" in the radial direction relative to an in-falling particle, and the amount of boost required goes to infinity at 2m.

 

As can be seen in the diagram, relative to the frame of a particle falling in from infinity, a hovering observer must be moving outward at near light velocity. Consequently his axial distances are tremendously contracted, to the extent that, if the value of Δr is normalized to his frame of reference, he is actually a great distance (perhaps even light-years) from the r = 2m boundary, even though he is just 1 inch above r = 2m in terms of the Schwarzschild coordinate r. Also, the closer he tries to hover, the more radial boost he needs to hold that value of r, and the more contracted his radial distances become. Thus he is living in a thinner and thinner shell of Δr, but from his own perspective there's a world of room. Assuming he brought enough rocket fuel to accelerate himself up to this "hovering frame" at that radius 2m + Δr (or actually to slow himself down to a hovering frame), he would thereafter just need to resist the local acceleration of gravity to maintain that frame of reference.

 

Quantitatively, for an observer hovering at a small Schwarzschild distance Δr above the horizon of a black hole, the radial distance Δrʹ to the event horizon with respect to the observer's local coordinates would be

 

 

which approaches  as Δr goes to zero. This shows that as the observer hovers closer to the horizon in terms of Schwarzschild coordinates, his "proper distance" remains relatively large until he is nearly at the horizon. Also, the derivative of Δrʹ with respect to Δr in this range is , which goes to infinity as Δr goes to zero. (These relations pertain to a truly static observer, so they don’t apply when the observer is moving from one radial position to another, unless he moves sufficiently slowly.)

 

Incidentally, it's amusing to note that if a hovering observer's radial distance contraction factor at r was 1−2m/r instead of the square root of that quantity, his scaled distance to the event horizon at a Schwarzschild distance of Δr would be Δrʹ = 2m + Δr. Thus when he is precisely at the event horizon his scaled distance from it would be 2m, and he wouldn’t achieve zero scaled distance from the event horizon until arriving at the origin r = 0 of the Schwarzschild coordinates. This may seem rather silly, but it’s actually quite similar to one of Einstein’s proposals for avoiding what he regarded as the unpleasant features of the Schwarzschild solution at r = 2m. He suggested replacing the radial coordinate r with ρ =, and noted that the Schwarzschild solution expressed in terms of this coordinate behaves regularly for all values of ρ. This just shows how easily we can “eliminate” poles and singularities simply by applying coordinates that have canceling zeros or by restricting the domain of the variables. However, we shouldn’t assume that every arbitrary system of coordinates has physical significance.

 

What "acceleration of gravity" would a hovering observer feel locally near the event horizon of a black hole? In terms of the Schwarzschild coordinate r and the proper time τ of the particle, the path of a radially free-falling particle can be expressed parametrically in terms of the parameter θ by the equations

 

 

where R is the apogee of the path (i.e., the highest point, where the outward radial velocity is zero). These equations describe a cycloid, with θ = 0 at the top, and they are valid for any radius r down to 0. We can evaluate the second derivative of r with respect to τ as follows

 

 

At θ = 0 the path is tangent to the hovering worldline at radius R, and so the local gravitational acceleration in the neighborhood of a stationary observer at that radius equals −m/R2, which implies that if R is approximately 2m, the acceleration of gravity is about −1/(4m). Thus the acceleration of gravity in terms of the coordinates r and τ is finite at the event horizon, and can be made arbitrarily small by increasing m.

 

However, this acceleration is expressed in terms of the Schwarzschild radial parameter r, whereas the hovering observer’s radial distance rʹ must be scaled by the “gravitational boost” factor, i.e., we have drʹ = dr/(1−2m/r)1/2. Substituting this expression for dr into the above formula gives the proper local acceleration of a stationary observer

 

 

This value of acceleration corresponds to the amount of rocket thrust an observer would need in order to hold position, and we see that it goes to infinity as r goes to 2m. Nevertheless, for any ratio r/(2m) greater than 1 we can still make this acceleration arbitrarily small by choosing a sufficiently large m. On the other hand, an enormous amount of effort would be required to accelerate the rocket into this hovering condition for values of r/(2m) very close to 1. This amount of “boost” effort cannot be made arbitrarily small, because it essentially amounts to accelerating (outwardly) the rocket to nearly the speed of light relative to the frame of a free-falling particle from infinity.

 

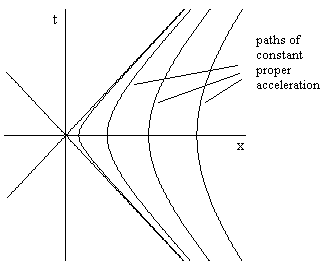
Interestingly, as the preceding figure suggests, an outward going photon can hover precisely at the event horizon, since at that location the outward edge of the light cone is vertical. This may seem surprising at first, considering that the proper acceleration of gravity at that location is infinite. However, although the proper acceleration of a photon is actually undefined (since a photon has no proper time), it can indeed be regarded as infinite, since the edge of a light cone can be regarded as hyperbolic motion with acceleration “a” in the limit as “a” goes to infinity, as illustrated in the figure below.

 

 

We've seen that the amount of local acceleration that must be overcome to hover at a radial distance r increases to infinity at r = 2m, but this doesn't imply that the gravitational curvature of spacetime at that location becomes infinite. The components of the curvature tensor depend to some extent on the choice of coordinate systems, so we can't simply examine the components of the Riemann curvature tensor to ascertain whether the intrinsic curvature is actually singular at the event horizon. For example, with respect to the Schwarzschild coordinates the non-zero components of the covariant curvature tensor are

 

 

along with the components related to these by symmetry. The two components relating the radial coordinate to the spherical surface coordinates are singular at r = 2m, but this is again related to the fact that the Schwarzschild coordinates are not well-behaved on this manifold near the event horizon. A more suitable system of coordinates in this region (as noted by Misner, et al) is constructed from the basis vectors

 

 

where γ = . With respect to this "hovering" orthonormal system of coordinates the non-zero components of the curvature tensor (up to symmetry) are

 

 

Of course, it isn’t possible to hover precisely at (or inside) the event horizon, but remarkably, if we transform to the orthonormal coordinates of a free-falling particle, the curvature components remain unchanged. Putting r = 2m, we see that these components are all proportional to 1/m2 at the event horizon, so the intrinsic spacetime curvature at r = 2m is finite. Indeed, for a sufficiently large mass m the curvature can be made arbitrarily mild at the event horizon. If we imagine the light cone at a radial coordinate r extremely close to the horizon (i.e., such that r/(2m) is just slightly greater than 1), with its outermost ray pointing just slightly in the positive r direction, we could theoretically boost ourselves at that point so as to maintain a constant radial distance r, and thereafter maintain that position, similar to how an outward-going photon can maintain it’s radial position precisely at the horizon. Clearly the work that must be expended for a massive particle to achieve this hovering condition from infinity cannot be made arbitrarily small, since it requires us to accelerate to nearly the speed of light. We’ve also seen that the amount of “rocket thrust” necessary for a material object to maintain it’s radial position goes to infinity for fixed radial positions near the horizon – which may seem paradoxical, since a photon hovering at the horizon is not expending any rocket thrust at all, it is simply coasting on its geodesic path. This might lead us to expect that a material object, having been accelerated to a hovering position very near the horizon (with an admittedly huge amount of effort), might be able to maintain its position thereafter with a fairly small amount of rocket thrust. In a sense, this is true, but only in terms of the natural coordinates (e.g., Schwarzschild coordinates) of a distant observer. An object hovering very close to the event horizon will be extremely red-shifted, i.e., will have a highly dilated proper time in terms of the distant observer’s coordinates. As a result, the distant observer would see the object expel a particle of rocket fuel only very infrequently, so the thrust would be very low as judged by the distant observer, even though in the proper time of the hovering object the rocket is ejecting material at a very high rate. In the case of a photon hovering at the horizon, the amount of time dilation is infinite, so to the distant observer the thrust is zero, whereas the photon itself has no proper time, so its proper thrust is undefined – consistent with the fact (mentioned above) that the photon’s proper acceleration is indeterminate, but can be taken to be infinite.

 

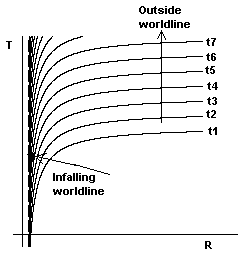
Having discussed the prospects for hovering near a black hole, let's review the process by which an object may actually fall through an event horizon. If we program a space probe to fall freely until reaching some randomly selected point outside the horizon and then accelerate back out along a symmetrical outward path, there is no finite limit on how far into the future the probe might return. This sometimes strikes people as paradoxical, because it implies that the in-falling probe must, in some sense, pass through all of external time before crossing the horizon, and in fact it does, if by "time" we mean the extrapolated surfaces of simultaneity for an external observer. However, those surfaces are not well-behaved in the vicinity of a black hole. It's helpful to look at a drawing like this:

 

 

This illustrates schematically how the analytically continued surfaces of simultaneity for external observers are arranged outside the event horizon of a black hole, and how the in-falling object's worldline crosses (intersects with) every timeslice of the outside world prior to entering a region beyond the last outside timeslice. The timeslices have the form tj − T = 2m ln(r/2m − 1) where T is the (inward) Eddington-Finkelstein time coordinate. We just repeat this same shape, shifted vertically, up to infinity. Notice that all of these infinitely many time slices curve down and approach the same asymptote on the left. To get to the "last timeslice" an object must go infinitely far in the vertical direction, but only finitely far in the horizontal (leftward) direction.

 

The key point is that if an object goes to the left, it crosses every single one of the analytically continued timeslice of the outside observers, all the way to their future infinity. Hence those distant observers can always regard the object as not quite reaching the event horizon (the vertical boundary on the left side of this schematic). At any one of those slices the object could, in principle, reverse course and climb back out to the outside observers, which it would reach some time between now and future infinity. However, this doesn't mean that the object can never cross the event horizon. It simply means that its worldline is present in every one of the outside timeslices. In the direction it is traveling, those time slices are compressed infinitely close together, so the in-falling object can get through them all in finite proper time (i.e., its own local time along the worldline falling to the left in the above schematic).

 

Notice that the temporal interval between two definite events can range from zero to infinity, depending on whose time slices we are counting. One observer's time is another observer's space, and vice versa. It might seem as if this degenerates into chaos, with no absolute measure for things, but of course there is an absolute measure. It's the absolute invariant spacetime interval "ds" between any two neighboring events, and the absolute distance along any specified path in spacetime is just found by summing up all the "ds" increments along that path. For any given observer, a local absolute increment ds can be projected onto his proper time axis and local surface of simultaneity, and these projections can be called dt, dx, dy, and dz. For a sufficiently small region around the observer these components are related to the absolute increment ds by the Minkowski or some other flat metric, but in the presence of curvature we cannot unambiguously project the components of extended intervals. The only unambiguous way of characterizing extended intervals (paths) is by summing the incremental absolute intervals along a given path.

 

An observer obviously has a great deal of freedom in deciding how to classify the locations of putative events relative to himself. One way (the conventional way) is in terms of his own time-slices and spatial distances as measured on those time slices, which works fairly well in regions where spacetime is flat, although even in flat spacetime it's possible for two observers to disagree on the lengths of objects and the spatial and temporal distances between events, because their reference frames may be different. However, they will always agree on the ds between two events. The same is true of the integrated absolute interval along any path in curved spacetime. The dt,dx,dy,dz components can do all sorts of strange things, but observers will always agree on ds.

 

This suggests that rather than trying to map the universe with a "grid" composed of time slices and spatial distances on those slices, an observer might be better off using a sort of "polar" coordinate system, with himself at the center, and with outgoing geodesic rays in all directions and at all speeds. Then for each of those rays he measures the total ds between himself and whatever is "out there". This way of "locating" things could be parameterized in terms of the coordinate system [θ, ϕ, β, s] where θ and ϕ are just ordinary latitude and longitude angles to determine a direction in space, β is the velocity of the outgoing ray (divided by c), and s is the integrated ds distance along that ray as it emanates out from the origin to the specified point along a geodesic path. (Incidentally, these are essentially the coordinates Riemann used in his 1854 thesis on differential geometry.) For any event in spacetime the observer can now assign it a location based on this system of coordinates. If the universe is open, he will find that there are things which are only a finite absolute distance from him, and yet are not on any of his analytically continued time slices. This is because there are regions of spacetime where his time slices never go, specifically, inside the event horizon of a black hole. This just illustrates that an external observer's time slices aren't a very suitable set of surfaces with which to map events near a black hole, let alone inside a black hole.

 

For this reason it's best to measure things in terms of absolute invariant distances rather than time slices, because time slices can do all sorts of strange things and don't necessarily cover the entire universe, assuming an open universe, as depicted in the above schematic, showing infinitely many external time slices. On the other hand, if the universe is closed and finite, there are only finitely many external time slices, and they eventually tip over and converge on a common singularity, as shown below

 

 

In this context the sequence of tj slices eventually does include the vertical slices. Thus, in a closed universe an external observer's time slices do cover the entire universe, which is why there really is no true event horizon in a closed universe. An observer could use his analytically continued time slices to map all events if he wished, although they would still make an extremely ill-conditioned system of coordinates near an approximate black hole.

 

One common question is whether a man falling (feet first) through an even horizon of a black hole would see his feet pass through the event horizon below him. As should be apparent from the schematics above, this kind of question is based on a misunderstanding. Everything that falls into a black hole falls in at the same local time, although spatially separated, just as everything in our city is going to enter tomorrow at the same time. We generally have no trouble seeing our feet as we pass through midnight tonight, although it is difficult one minute before midnight trying to look ahead and see our feet one minute after midnight. Now, for a small black hole we will have to contend with tidal forces that may induce more spatial separation between our head and feet than we'd like, but for a sufficiently large black hole we should be able to maintain reasonable point-to-point co-moving distances between the various parts of our body as we cross the horizon.

 

On the other hand, we should be careful not to understate the physical significance of the event horizon, which some authors have a tendency to do, perhaps in reaction to earlier over-estimates of its significance. In addition to its undeniable global significance, there is a sense in which (depending on the terms that are given ontological status) spacetime actually can be regarded as locally singular at r = 2m, even in terms of the proper time of an in-falling particle, although it is a "removable singularity", much like the point x = 0 on the function sin(x)/x. Strictly speaking this "curve" is undefined at that point, but by analytic continuation we can "put the point back in", essentially by just defining sin(x)/x to be 1 at x = 0. Whether nature necessarily adheres to analytic continuation in such cases is another question.

 

Finally, we might ask what an observer would find if he followed a path that leads across an event horizon and into a black hole. In truth, no one really knows how seriously to take the theoretical solutions of Einstein's field equations for the interior of a black hole, even assuming an open infinite universe. For example, as discussed in Section 6.4, the "complete" maximally extended Schwarzschild solution actually consists of two separate universes joined together at the black hole, but it isn't clear that this topology would spontaneously arise from the collapse of a star, or from any other known process, so many people doubt that this complete solution is ever actually realized in nature. It's just one of many strange topologies that the field equations of general relativity would allow, but we aren't required to believe something exists just because it's a solution of the field equations. On the other hand, from a purely logical point of view, we can't rule them out, because there aren't any outright logical contradictions.

 

Return to Table of Contents