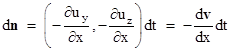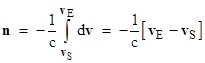Stokes’ Mistake

The original interpretation of stellar aberration when it was first discovered by Bradley was in terms of a corpuscular theory of light, but when the wave theory gained prominence in the 19^th century the explanation for stellar aberration became more difficult. The basic problem was that no one knew if the putative luminiferous ether was immobile or participated in the motions of ordinary material objects. On the assumption that it was just slightly dragged along by ordinary objects, Fresnel had given a fairly successful account of aberration and other first order optical phenomena, but many physicists were dissatisfied with the idea that the ether was so little affected by ordinary matter.

In 1845 George Gabriel Stokes (1819-1903) sought to interpret the effect of stellar aberration in terms of an ether that was totally dragged along with material bodies. He assumed that, for macroscopic frequencies, the ether acted as an incompressible and irrotational fluid with no viscosity (and hence no drag), and that the ether’s velocity matches the velocity of any solid object at the boundary of the object. On the basis of these assumptions he derived the amount by which incoming plane waves would be tilted due to the flow of the carrying medium, and found that the result matched the observed aberration of starlight. However, Hendrik Lorentz later pointed out that Stokes’ premises are mutually exclusive, because the velocity field of a potential flow past a spherical object does not match the sphere’s speed at the boundary. Nevertheless, it’s interesting to review the derivation, to understand precisely how the a flow field with a velocity potential leads to deflection of rays.

Consider a portion of a plane wave, centered at the origin of xyz coordinates, with the normal pointing in the positive x direction as shown below.

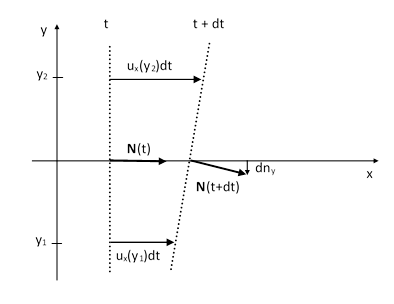
Since the wave is assumed to be propagating through the ether, and the ether itself is moving (relative to the frame of the quiescent background ether far from any bodies), the wavefront acquires additional components of velocity from the ether. If the motion of the ether varies from place to place, it can have the effect of tilting the wavefronts. To the first order the only significant effects are due to the component of the ether’s velocity in the direction of the wave propagation. Thus, letting u = [u_x,u_y,u_z] denote the velocity vector of the ether, we will focus on the component u_x(x,y,z). In the xy plane the motion of a wave front from the time t to the time t + dt is illustrated below.

This shows that if the x-component of the ether speed is increasing with y, then the wavefront will be tilted downward, i.e., toward the direction of decreasing y. This tilt can be represented by an increment dy applied to the normal vector N at time t to give the new normal vector N at time t + dt. Likewise we can determine the tilt in the z direction based on the partial derivative of u_x with respect to z. Quantitatively we have

Changes in u_x with respect to x don’t have any first-order tilting effect, so these are the only two components that contribute to tilting the wavefront. Thus the incremental deviation of the normal vector is a vector parallel to the yz plane

At this point we face the seemingly challenging task of integrating these incremental deviations over the entire path of the wave from the emitting star to the Earth. In addition, it may seem unlikely to yield an answer that agrees with observation, because these equations involve just the derivatives of the speed component u_x of the ether in the direction of the wave, whereas the aberration angle ought to be determined by the transverse components u_y and u_z of the ether. However, at this point Stokes assumed the ether is incompressible (so that the speed of light is homogeneous), inviscid (to avoid drag), and irrotational. The latter assumption ensures that the ether supports a velocity potential. By definition the vorticity is zero in an irrotational fluid, so we have

Thus the incremental tilting vector can be written as

where the transverse ether velocity v is the projection of the ether velocity vector u onto the yz plane (i.e., transverse to the direction of the wave). Since dx/dt = c to the first order, we have

Integrating this from the far field where the transverse ether velocity is v_S to the surface of the Earth where the transverse ether velocity is v_E, we get the total angular deflection

Now Stokes assumed the speed of the ether relative to the Earth was zero at the Earth’s surface, so we have v_E = 0 and therefore the deviation vector is n = v_S/c. The magnitude of v_S is simply sin(θ) times the magnitude of u_S, where θ is the elevation angle of the star, so the aberration angle is given by

in agreement with observation.

Unfortunately, as Lorentz pointed out, there is a serious flaw in this reasoning. Potential flow past a sphere does not result in zero relative flow velocity at the surface of the sphere. The flow velocity at the surface is parallel to the surface, but it is non-zero, and varies significantly from one point to another on the surface. Therefore, if the luminiferous ether was a fluid of the type assumed by Stokes, the aberration of starlight would differ significantly from what is observed. Any variation of Stokes’ assumptions in order to achieve zero surface velocity, such as Planck’s suggestion of allowing the ether to be compressible, also introduces other effects that invalidate the above analysis and lead to aberration angles that differ from what is observed. Therefore, Stokes’ theory of a completely dragged ether was unsuccessful.

Oddly enough, many popular attempts to explain aberration in terms of a totally dragged fluidic ether are even more seriously flawed than Stokes’ theory. They typically imagine simple transverse sliding between layers of the ether, with the incoming rays deflected accordingly. There are two problems with this simplistic explanation. First, with only transverse motion there is no tilting of the wavefronts, so this is really just a disguised ballistic theory rather than a true wave theory. (See Stellar Aberration for a fuller account of this distinction.) Second, although it’s possible to arrive at the correct magnitude of aberration with this approach, the proponents of this explanation tend to overlook the fact that it predicts aberration in the opposite direction from what is actually observed.

Incidentally, Lorentz’s derivation of the aberration angle in Stokes’ model, although it arrives at the correct conclusion, contains a little slight of hand. The derivation in Lorentz’s book “Theory of Electrons” begins by saying that a particle of ether at the point (x₀,y₀,z₀) at time t will have moved after an increment of time dt to the point with coordinates

Lorentz then notes that the velocity components (in any small region) can be expressed at linear functions of the coordinates, so we have (for example)

for a small region around a given particle. In this expression the origins of the x,y,z coordinates are subsumed in the constant α. Of course, the constants β, γ, and δ are just the partial derivatives of u_x with respect to x, y, and z respectively. Substituting this expression for u_x into the equation for x₁, he gets

He then considers the set of points beginning on the plane x = a with various values of y and z, to determine the new plane formed by these points after a time dt. Thus we have x₀ = a, and Lorentz says we might as well substitute x₁,y₁,z₁ in place of x,y,z because the partial derivatives don’t change much over this incremental distance. After making these substitutions, he re-write the equation in the form

and from this he concludes the direction cosines of the normal to the plane of particles at the time t + dt are proportional to the coefficients (1−βdt), −γdt, and –δdt. This agrees with the y and z components we derived previously, but what are we to make of the x component? This was reached by replacing x with x₁ in the previous equation, but we could just as well have set x = x₀, in which case the coefficient of x₁ would be simply 1. Essentially the normal to the plane (to the first order in u/c) is independent of how the ether speed in the x direction changes as a function of x, because this simply advances the entire wavefront at the same rate. Thus the partial derivative of u_x with respect to x has no effect on the tilting vector. It’s convenient to include this component in the formulation, as Lorentz did, because it enables us to deal with the entire velocity vector u, without needing to introduce the projection of this vector onto the yz plane, but it works only because the effect of the x component is negligible.

Return to MathPages Main Menu