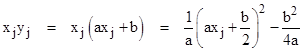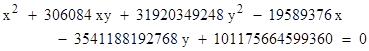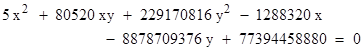No Progression of Four Rectangles On A Conic?

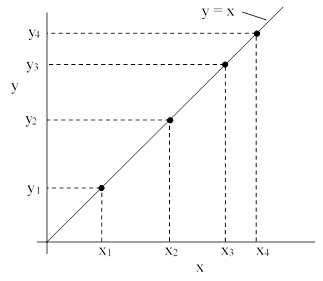
As discussed in a previous note, there are no four squares in arithmetic progression. This fact can be expressed in terms of lattice points on the diagonal line x = y as shown in the figure below.

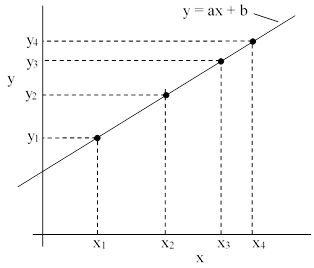
Thus we can express the non-existence of four squares in arithmetic progression by saying that there do not exist four points with integer coordinates (x_j,y_j), j = 1,2,3,4, on the line y = x such that the four products x_jy_j are in arithmetic progression. This fact can be immediately generalized to lattice points on an arbitrary line y = ax + b for rational coefficients a,b with a ≠ 0, as depicted in the figure below.

To prove that the four products x_iy_i cannot be in arithmetic progression, simply note that

which shows that if these four quantities are in arithmetic progression then we can add b²/(4a) to each number and multiply each number by “a”, giving four rational squares in arithmetic progression, which we’ve already seen is impossible.

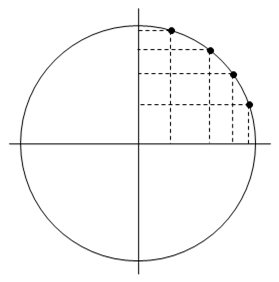
Can this proposition be generalized any further? The note entitled Discordance Impedes Square Magic included a table of sets of three right triangles with rational edge lengths on a common hypotenuse and with areas in arithmetic progression, but it’s easy to show that no four such triangles exist. This implies that there do not exist four lattice points on a circle such that the areas of the corresponding rectangles are in arithmetic progression, as shown below.

Let the rational number Q denote the squared radius of the circle, so the locus containing the four point is x² + y² = Q. For any four such points x_i,y_i, i = 1,2,3,4 with integer coefficients, the areas xy cannot be in arithmetic progression. To prove this, note that if four such points exist then

for each I, and hence if the four quantities xiyi are in arithmetic progression, so are the four squares (x_i – y_i)², which we’ve already seen is impossible.

Generalizing even further, we may conjecture that for any rational numbers a, b there do not exist positive integers x_j,y_j, j = 1,2,3,4 such that

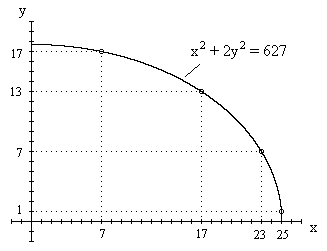
for j = 1,2,3,4 and such that the four products (x_j y_j) are in arithmetic progression. In other words, for any four points (x_j,y_j) with integer coordinates on the conic x² + ay² = b the four rectangles with those edge lengths cannot have areas in arithmetic progression. To illustrate, consider four rectangles inscribed in a quadrant of an ellipse as shown below.

In this figure the four rectangles inscribed in the ellipse x² + 2y² = 627 have the edge lengths (25,1), (7,17), (23,7) and (17,13), so the four rectangular areas are 25, 119, 161, and 221. Obviously these are not in arithmetic progression. The conjecture is that no four rectangles with integer edge lengths inscribed in a quadrant of a central conic can have areas in arithmetic progression.

With b = 0 the conic degenerates to a straight line x² = ay². In this case the coefficient “a” must be a square, so it can be absorbed into y, and we have simply x² = y² and thus (in the first quadrant) x = y. The four rectangles are therefore squares, and the conjecture is equivalent to the well-known theorem on four squares. On the other hand, with a = 1 and b equal to an arbitrary positive integer constant, this gives the fact that no four rectangles (with integer edges) on a common diagonal can have areas in arithmetic progression.

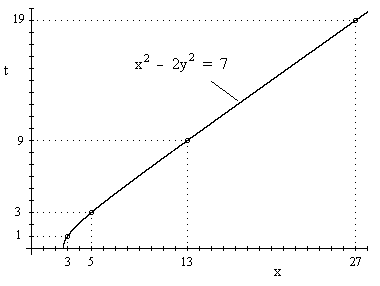
Another family of cases is given by setting a = -N and b = D, so the x,y pairs are solutions of a single Pell equation. x² – Ny² = D. In this case the conic is a hyperbola, as shown in the figure below with a = -2 and b = 7.

In general the integer solutions of Pell equations grow exponentially, so the areas corresponding to successive solutions could not be expected to be in arithmetic progression. However, there can be multiple exponential sequences, so the assertion that no four are in arithmetic progression is non-trivial. For example, in the case depicted above, there are two solution sequences, with x values 3, 13, 75, … and 5, 27, 157, …

Of course, the expression x² + ay² = b can be written as

so the conjecture would follow for any value of the constant “a” such that the proof of no four squares in arithmetic progression applies to the field of quadratic numbers of the form .

The conjecture could be extended to fully arbitrary conics. In other words, we may conjecture that for any conic

with rational coefficients there do not exist four integer solutions (x_j,y_j), j = 1,2,3,4 such that the four products x_jy_j are in arithmetic progression. One configuration is depicted in the figure below.

Of course, the conjecture is easily seen to be true for any conic of the form

since in this case the fact that the four values of xy are in arithmetic progression automatically implies that the four values of x² are in arithmetic progression, which we’ve already shown is impossible for integers.

Incidentally, the restriction to rational coefficients is necessary, because the proposition would certainly be false if we allowed the coefficients of the conic to have any real values. This is because any four points on the plane can be fit to a parabola, or, if one point is inside the triangle formed by the other three, to a hyperbola. (See the notes entitled Parabola Through Four Points and Revisiting the Four Point Parabola.) It might be interesting to examine the family of parabolas (and hyperbolas) that pass through sets of four points in arithmetic progression, to see if it can be proven that the coefficients of such conics are necessarily irrational.

Update:  The basic conjecture discussed above concerned central conics, and that conjecture remains open. However, the extended conjecture for arbitrary conics has been disproven. In a note entitled "Arithmetic progressions of rectangles on a conic" appearing in "Notes on Number Theory and Discrete Mathematics" (Vol 20, 2014), Ajai Choudhry derived explicit expresions for an infinite family of parabolas, each with five points whose coordinate products are in arithmetic progression, and for ellipses and hyperbolas with six points whose coordinate products are in arithmetic progression. His solution gives (for example) the parabola

which contains the five point (24,30), (28,30), (30,32), (30,36), (24,50) such that the coordinate products 720, 840, 960, 1080, and 1200 are in arithmetic progression. He also gives (as another example) the ellipse

which contains the six points (2088672,39), (1674504,52), (7724184,12), (8192184,12), (1998504,52), (8426016,13) such that the coordinate products 81458208, 87074208, 92690208, 98306208, 103922208, 109538208 are in arithmetic progression. Lastly, he presents the example of a hyperbola

which contains the six points (38208,15), (53712,10), (83520,6), (77520,6), (42912,10), (78624,5) such that the coordinates products 573120, 537120, 501120, 465120, 429120, and 393120 are in arithmetic progression. Choudhry says this leaves open the question of whether there exist parabolas with six points, or ellipses or hyperbolas with seven points, whose coordinate products are in arithmetic progression. In view of these results, it would be interesting to know, for any specific conic, the length of the longest arithmetic progression of coordinate products.

The existence of general conics with more five (or six) points in progression was perhaps to be expected, since one could begin with a central conic with three points in progression and then add two more free parameters (the coefficients of x and y). The number of degrees of freedom of a general conic makes it likely that some could be found with more than three points in progression. In contrast, the central conics have two fewer degrees of freedom, so the basic conjecture seems more likely to be true.

Return to MathPages Main Menu