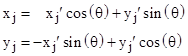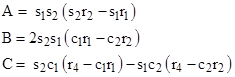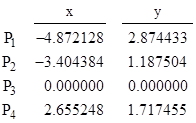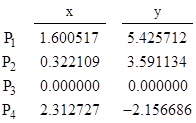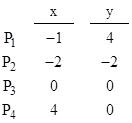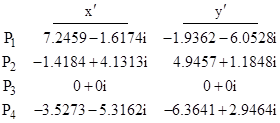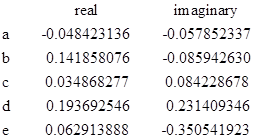Parabola Through Four Points

Any four points in the plane determine two conjugate parabolas, each of which passes through all four points. Of course, the axis of these parabolas aren't necessarily parallel to the y axis. Given the points P_j with coordinates (x_j,y_j) for j = 1,2,3,4, we are free to translate the coordinate system so that x₃ = y₃ = 0. In terms of this coordinate system we can fit a second degree polynomial to the three points P₁,P₃,P₄. Since P₃ is at (0,0) this polynomial has the form

Similarly we can fit a second degree polynomial to the three points P₂,P₃,P₄. This polynomial will be of the form

The coefficients c₂ and d₂ are given by

The numerators of these coefficients are invariant under rotations but the denominators are not. Thus, if we rotate the coordinate system relative to the configuration of points, we can vary the values of c₂ and d₂. There exists a particular orientation in which c₂ = d₂, and for this orientation the difference between the two parabolas is Δy′ = (c₁ – d₁)x′, which is a straight line that passes through zero x₃′ and x₄′, and hence is identically zero. Therefore, the two parabolas are the same, so this is the orientation for which a single polynomial of degree 2 passes through all four points.

The original coordinates x,y are related to the rotated coordinates x′,y′ by a transformation of the form

for some angle θ. Substituting for x and y into the expressions for c₂ and d₂, and setting c₂ = d₂, we arrive at a quadratic equation of the form

If we choose our (arbitrary) initial orientation and scale factor such that x₄ = 1 and y₄ = 0 then the coordinates of this quadratic are simply

The two roots of the quadratic give the two orientations in which the four points lie on a single second degree polynomial. (Incidentally, this shows that if a parabola with vertical axis intersects a horizontal line at points P,Q, and a second parabola intersects the first at the points P,Q,R,S, then the slope of the second parabola's axis is half the slope of the line through R,S.)

In general, given the coordinates of any four distinct points, we can express the configuration in purely relative terms (since the position and orientation don’t matter), e.g., as the lengths of the three segments

and the angles

If we let s_j and c_j denote the sine and cosine of θ_j, then the angle theta that the ray P₃ – P₄ must make with the positive x axis in order for the four given points to lie on a single parabola must satisfy the quadratic

where

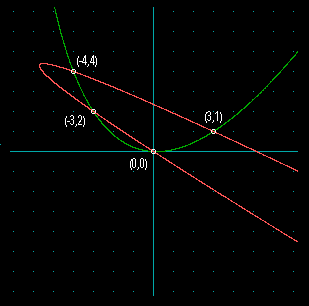
As an example, consider the four points (–4,4), (–3,2), (0,0), and (3,1). This relative configuration of points can be represented by

To make a single parabola pass through all four points we must place P₃ at the origin and orient the set of points such that the segment P₃ - P₄ makes an angle of either 0.574133 or –0.750499 radians with the positive x axis. In our original coordinate system we had P₄ at (3,1), so the angle between P₃ - P₄ and the x axis was atan(1/3), which equals 0.32175055, so this means we have to rotate those four points from that configuration by either –0.252382 radians or 1.072250 radians. (Note that the signs of the angles are negated, because θ was defined as the angle from the transformed coordinates to the original coordinates, whereas now we are rotating from the original to the transformed.) In the first case the coordinates of the four points become

and the parabola that passes through those points is

In the second case the coordinates of the four points become

and the parabola that passes through those points is

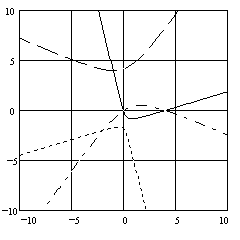
We can transform both of these parabolas back to the original coordinate system, and show how both general parabolas pass through all four points. This is illustrated in the figure below.

This method can evidently be applied to give the parabola passing through any four distinct points, and yet one may wonder how it's possible for a single parabola to pass through each of the four points in a configuration such as shown below:

In general, if any of the points falls inside the triangle formed by the other three, then we can still find the parabola that contains all four points, but in such cases the parabola's coefficients are complex. As an example, consider the four points with the following coordinates

Here the point P₃ falls inside the triangle formed by P₁,P₂,P₄. Using the formula given above, this leads to the equation

where θ is the angle through which the xy coordinate axes must be rotated (counter clockwise) to give a coordinate system in which all four points lie on a single polynomial of degree 2. Solving this for theta gives the two complex solutions

Both of these roots correspond to

In the rotated coordinate system x'y', the coordinates of the four points are

The second degree polynomial that passes through all four points is

where

In the original xy coordinate system we have the following equation for this conic

where

with

Since b² = 4ac, this conic is formally a parabola. For our example, the real and imaginary parts of the conic coefficients are as shown below.

It's interesting that the real and imaginary parts of these parabola coefficients, taken separately, give two real conics (hyperbolas), each of which passes through all four points as shown below.

For more on this topic, see Revisiting the Four-Point Parabola.

Return to MathPages Main Menu