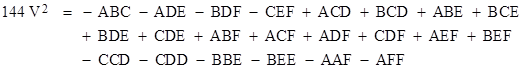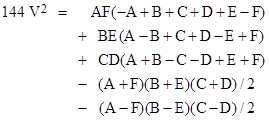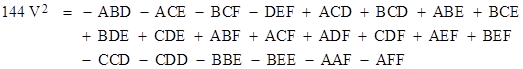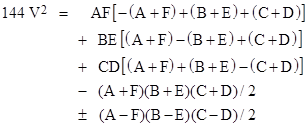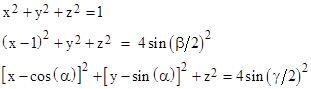Piero della Francesca's Tetrahedron Formula

The painter Piero della Francesca (who died on Oct 12, 1492, the same day Columbus sighted land on his first voyage to America) also studied mathematics, and one of his results leads to a 3-dimensional analogue of Heron's formula for the volume of a general tetrahedron with edges a,b,c,d,e,f, taken in opposite pairs (a,f), (b,e), (c,d).  Letting A,B,..,F denote the squares of these respective edge lengths, his formula was

This polynomial doesn't factor, but it can be expressed as a sum of five "squared volume terms" as follows:

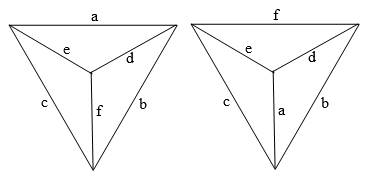
(Can the formula be broken down into fewer than 5 terms, where each "term" is a product of three linear functions of the squared sides?) It's interesting to note that there are really two distinct shapes (up to rotations and reflections), with distinct volumes, for any given set of six edge lengths and opposite pair assignments.  In other words, there are two distinct shapes for any given choice of "pairings" depending on how we choose to connect those pairs.  To illustrate, for the non-intersecting pairs {a,f}, {b,e}, and {c,d} we have the following two distinct tetrahedral graphs

The only change has been to transpose the edges a ↔ f, but notice that in the left-hand figure the edge "a" meets the edges c,e at one end and b,d at the other, whereas in the right-hand figure it meets the edges b,c at one end and d,e at the other. These two distinct configurations are can be seen algebraically in the volume formulae.  Piero's formula corresponds to the arrangement on the left, whereas the volume of the tetrahedron on the right would be given by

This is close to Piero's formula, but not exactly the same.  Where Piero had the four leading terms

this formula has

Actually both formulas are correct, but they represent the two distinct tetrahedrons that can be constructed from six given edges with given pairings of non-intersecting edges (a,f), (b,e), (c,d). This appears most clearly if we consider again Piero's volume formula expressed as a sum of five "squared volume" terms, written in the slightly different form

The first four terms are symmetrical in the non-intersecting pairs, but the fifth term is anti-symmetric, i.e., it reverses sign when we transpose any of the pairs.  This is why we’ve placed a ± sign on that term.  With the - sign it gives Piero's formula, whereas with the + sign it gives the volume for the "conjugate" tetrahedron.  So this formula represents the two possible tetrahedron volumes (and shapes) for a given pairing of the edges.

The entire expression is symmetrical under permutations of the three pairs, so for a given set of six edge lengths (all satisfying the triangle inequality with respect to each other) the number of distinct pairings is (5)(3)(1) = 15, and for each of these there are two distinct tetrahedra, so there are a maximum of 30 distinct tetrahedra (with distinct volumes) that can be constructed from six given edges.

The four terms in which the two formulas differ

are precisely the four triangular faces of the respective tetrahedra. In other words, the first tetrahedra has the four faces (a,b,c), (a,d,e), (b,d,f) and (c,e,f), whereas the conjugate tetrahedron has the faces (a,b,d), (a,c,e), (b,c,f), and (d,e,f).

Of course, we can easily express the volume of an arbitrary tetrahedron by the usual formula in terms of the three edge vectors a, b, c emanating from a single vertex

where "." signifies the dot product and "x" is the cross product.  This is easy to see if we recall that the area of the triangle with edges b,c is (bc/2)sin(α) where α is the angle between the edge vectors b and c.  Also, the height of the pyramid on this base is  (a)cos(θ_a) where θ_a is the angle between the vector a and the perpendicular to b and c.  Then, since the volume of any pyramid is 1/3 the base times the height, we have

where ϕ_a is the angle between a and the plane of b and c.  Naturally this is consistent with the magnitudes of the dot and cross products. By symmetry, if we define β, γ, ϕ_b, and ϕ_c similarly to α and ϕ_a, the above implies that

for any three vectors a, b, c, because this is proportional to the subtended volume, just as sin(α) is proportional to the subtended area.  Hence, in a sense, this quantity sin(α)sin(ϕ_a) is the natural three-dimensional analog of the two-dimensional sine function.

Incidentally, suppose we want to express the standard formula

entirely in terms of the cosines of the angles α, β, γ between the three edges a, b, c emanating from a point.  Consider unit vectors on the three edges, with the vertex at the origin of xyz coordinates and make one of the vectors [1,0,0] and another [cos(α), sin(α), 0].  Since the distance between two points on a unit sphere equals twice the sine of the half-angle between them, the unit vector [x,y,z] along the third edge must satisfy the conditions

Substituting 1 – x² – y² for z² in the second equation gives

and substituting this into the third equation gives

Substituting back into z² = 1 – x² – y², multiplying through by sin(α)², and noting that z = sin(ϕ_a), we have

This formula is well known. (See, for example, the discussion of rational tetrahedra in Dickson's history of the theory of numbers, which refers to a paper by K. Schwering in 1895.) If we substitute the expressions for the cosines in terms of the edge lengths (see the note on Heron's Formula) into the above expression, we recover Piero's formula.  For more on tetrahedron volume formulas, see Heron's Formula for Tetrahedrons, and also the note on the Cayley-Menger determinant.

Return to MathPages Main Menu