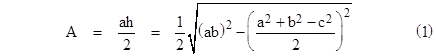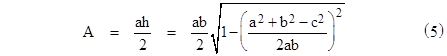Heron's Formula and Brahmagupta's Generalization

Let a,b,c be the sides of a triangle, and let A be the area of the triangle. Heron's formula states that A² = s(s – a)(s – b)(s – c), where s = (a + b + c)/2. The actual origin of this formula is somewhat obscure historically, and it may well have been known for centuries prior to Heron. For example, some people think it was known to Archimedes. However, the first definite reference we have to this formula is Heron's. His proof of this result is extremely circuitous, and it seems clear that it must have been found by an entirely different thought process, and then "dressed up" in the usual synthetic form that the classical Greeks preferred for their presentations.

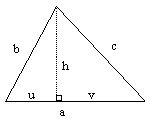
Here's a much more straightforward derivation. Consider the general triangle with edge lengths a,b,c shown below

We have a = u+v, b² = h² + u², c² = h² + v². Subtracting the second from the third gives u² – v² = b² – c². Dividing both sides by a = u + v, we have u – v = (b² – c²)/a. Adding u + v = a to both sides and solving for u gives

Since h is the square root of b² – u² we have

which is equivalent to Heron's formula. Factoring out 1/4, this gives three different ways of expressing (2ab)² – (a² + b² – c²)² as a difference of two squares. Equivalently, it gives three different factorizations of 16A², each of the form

Factoring each of these terms gives the explicitly symmetrical form

so if we define s = (a + b + c)/2 we can write equation (1) as

which is the area formula as given by Heron. For an alternative derivation see Heron’s Formula for Tetrahedra.

Incidentally, if we factor ab out of the radical in equation (1) we get

Notice that if we take either the edge "a" or "b" as the base of the triangle, then the height is sin(θ) where θ is the angle between "a" and "b", and of course the area of half the altitude times the base (which is easily seen by considering the parallelogram), so we have A = (ab/2) sin(θ), which implies that the radical in (5) equals the sine of the angle between "a" and "b". Of course, it also implies that the cosine is given by the well-known formula

By the way, permutations of {a,b,c} = {3,5,7} in equation (2) give the three factorizations 675 = (15)(45) = (9)(75) = (5)(135), which leaves out (1)(675), (3)(225), and (25)(27). Is there an expression in a,b,c that gives these three factorizations under permutation?

One of the most beautiful things about Heron's formula is the generalization discovered by the Hindu mathematician Brahmagupta around 620 AD. He noted that we have a symmetrical product of four factors inside the square root of equation (4), consisting of twice the quantities

In a sense we can "fill out" the symmetry, making each of the four factors symmetrical with the others, by imagining a fourth "side" of length d = 0 being subtracted from the first factor and added to the remaining three, so we have

Obviously with d = 0 this is identical to the previous set of factors, but it has greater formal symmetry, so it seems as if the quantity

must represent... something meaningful… and indeed it does. This is the area of a quadrilateral with sides a,b,c,d inscribed in a circle, i.e., a cyclic quadrilateral. Naturally every triangle is cyclic, meaning that it can be inscribed in a circle, and a triangle can be regarded as a quadrilateral with one of its four edge lengths set equal to zero. Brahmagupta didn't actually give a formal proof of this result, and in fact the surviving copies of his statement of this proposition don't mention the fact that it applies only to cyclic quadrilaterals. It's tempting to think that Brahmagupta might have just imagined the equation based on its formal symmetry.

Incidentally, the formula for the area of an arbitrary quadrilateral is

where α is half the sum of two opposite angles. For a cyclic quadrilateral each pair of opposite angles sums to π, so it reduces to Brahmagupta's formula.

Return to MathPages Main Menu