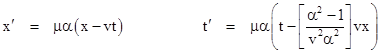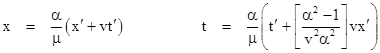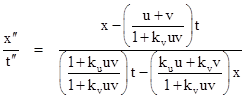A Primer on Special Relativity

An inertial coordinate system is defined as a system of space and time coordinates in terms of which the resistance to acceleration of any given object at rest is the same at every location and in all directions. In other words, we define inertial coordinate systems in such a way that the inertia of material objects is homogeneous and isotropic. Homogeneity implies that every material particle free of external influence moves at constant speed in a straight line (i.e., the space coordinates are linear functions of the time coordinate), and isotropy implies that if two identical material particles initially adjacent and at rest act to repel each other, they acquire equal speeds (i.e., derivatives of the space coordinates with respect to time) in opposite directions. Given one inertial coordinate system we can construct infinitely many others by means of arbitrary fixed translations and spatial re-orientations, which leave the speed of every object unchanged. Such an equivalence class of inertial coordinate systems is called an inertial reference frame.

It's important to note that the definition of an inertial reference frame given above not only identifies inertial motion with straight paths of constant speed, it also establishes an operational definition of simultaneity (i.e., the synchronization of times at spatially separate events), because inertial isotropy implies that we can use identical physical objects acting against each other to synchronize clocks equidistant from their center of mass (relying on either inertial oscillations or the equilibrium configurations of solid objects at rest to define distances). Unfortunately the terms “inertial coordinate system” and “inertial reference frame” are often defined in a weaker sense, based simply on homogeneity, without requiring isotropy. This weaker definition identifies inertial coordinate systems with unaccelerated coordinate systems. It is obviously permissible to make such a definition, but we must recognize that inertia need not be isotropic with respect to unaccelerated systems of coordinates. There is an unfortunate tradition in text books to define inertial coordinates merely as unaccelerated, i.e., such that (classically) Newton’s first law holds good, and then to immediately assert that all of Newton’s laws hold good with respect to such coordinates. This is not generally true, because the set of space-time coordinate systems in terms of which Newton’s first law holds good is much larger than the set of coordinate systems in terms of which all of Newton’s laws hold good. In order to identify the latter systems, we must stipulate not just inertial homogeneity but also inertial isotropy. A more suitable name for these systems of reference might be something like “inertia-based” rather than “inertial”, since the latter word is so suggestive of the word “unaccelerated”. On the other hand, the term “inertial coordinate system” is widely used to refer to systems for which inertia is both homogeneous and isotropic – even though it is rarely defined that way. We have chosen here to actually define the term in such a way that it corresponds to the most widely held meaning. See the note “What is an Inertial Coordinate System?” for a more detailed discussion of the sources of this troublesome linguistic and conceptual confusion.

Given the above definition of inertial reference frames, the principle of relativity asserts that for any material particle in any state of motion there exists an inertial reference frame – called the rest frame of the particle – with respect to which the particle is instantaneously at rest (i.e., the change of the spatial coordinates with respect to the time coordinate is zero). This principle is usually extended to include reciprocity, meaning that for any two suitably aligned systems S₁ and S₂ of inertial coordinates, if the spatial origin of S₁ has velocity v with respect to S₂, then the spatial origin of S₂ has velocity –v with respect to S₁. The existence of this class of reference frames, and the viability of the principles of relativity and reciprocity, are inferred from experience. Once these principles have been established, the relationship between relatively moving inertial coordinate systems can then be considered.

Let [t,x,y,z] signify a system of inertial coordinates in the rest frame of particle p, and likewise let [t′,x′,y′,z′] signify a system of inertial coordinates in the rest frame of a particle p' moving with speed v relative to [t,x,y,z]. By means of a fixed translation we can make the origins of these two coordinate systems coincide, and by a fixed spatial rotation we can spatially align the x and x′ axes.  For simplicity, we will consider particles and motions confined to the x,x′ axes. The question naturally arises as to how these two coordinate systems are related to each other for a given relative velocity v. Since, by definition, inertial motions are straight lines with respect to both systems (and since we require that continuously varying coordinates map to continuously varying coordinates, thereby ruling out linear fractional transformations), the relations between two inertial coordinate systems must be linear functions of the form

for constants A,B,C,D (for a fixed v). A stationary object in the rest frame of p′ has a constant value of x′, so the differential dx′ = Adx + Bdt = 0 implies dx/dt = –B/A = v and hence B = –vA. The inverse of the above transformation is

Evaluating the velocity of a stationary object in the frame of p with respect to the frame of p' leads to dx′/dt′ = B/D = –v (by reciprocity) and hence D = A.

Letting μ² denote the quantity AD - BC, and substituting for B and D, we have A² + vAC = μ², so we have C = (μ² - A²)/(vA). If we define α = A/μ, then the original transformation can be written in the form

and the inverse transformation has the form

If we replace v with –v these two transformations are exchanged, except for the factor μ, so if we are to have spatial isotropy we must have μ equal to 1. This leaves undetermined only the expression in square brackets. (Remember that the parameter α is a function of v, but it is a constant for any fixed v.) Letting k denote this quantity, we have [(α²-1)/(vα)²] = k, from which we get , and the general transformation can be written in the form

Any two inertial coordinate systems must be related by a transformation of this form, where v is the mutual speed between them. Also, note that

Given three systems of inertial coordinates with the mutual speed v between the first two and u between the second two, the transformation from the first to the third is the composition of transformations with parameters k_v and k_u. Letting x″,t″ denote the third system of coordinates, we have by direct substitution

The coefficient of t in the denominator of the right side must be unity, so we have k_u = k_v, and therefore k is a constant for all v, with units of an inverse squared speed. Also, the coefficient of t in the numerator must be the mutual speed between the first and third coordinates systems. These identifications are necessary and sufficient to make the transformation be of the required form.

Now, if k is non-zero, we can make its magnitude equal to unity by a suitable choice of units for distance and time, so the only three essentially distinct cases to consider are k = –1, 0, or +1. If k = –1 this transformation is simply a Euclidean rotation in the xt plane through an angle θ = invtan(v). In other words, with k = –1 the above equations can be written in the form

On the other hand, with k = 0 the general transformation reduces to the Galilean space-time transformation, i.e., we have

The remaining case is with k = +1, which gives the so-called Lorentzian transformation

We wish to determine which of these represents the correct relation between relatively moving inertial coordinate systems. The Euclidean transformation (i.e., the case k = –1) is easy to rule out empirically, because we cannot turn around in time as we can in space. However, it isn't as easy to distinguish empirically between the Galilean and Lorentzian transformations, especially if the value of k in ordinary units of space and time is extremely close to zero. As a result, Newtonian mechanics was based for many years on the assumption that k = 0.

It was not until the late 19th century that sufficiently precise experimental techniques became available to determine that the true value of k is not zero. In ordinary units it has the value (1.11)10^–17 second²/meter² (which happens to equal 1/c² where c is the speed at which electromagnetic waves propagate in vacuum). This implies that relatively moving systems of inertial coordinates are related according to the Lorentzian transformation. It follows that the constant-t surfaces of two relatively moving systems of inertial coordinates are skewed, although the skew is so slight it's nearly impossible to detect in most ordinary circumstances.

It was also found that Maxwell’s equations of electromagnetism – which were developed without knowledge of the Lorentz transformation – are actually invariant with respect to the Lorentz transformation. Hence all the phenomena of electromagnetism and of mechanical inertia are relativistic with respect to precisely the same class of transformations. Furthermore, it was found that whatever forces are responsible for the stability of matter (which was known to be inexplicable in terms of classical electromagnetism alone) are also invariant with respect to the Lorentz transformation. Naturally this led to the hypothesis that all physical phenomena are (at least locally) invariant with respect to the Lorentz transformation. Subsequently this hypothesis has been confirmed for the strong and weak nuclear forces and for all quantum mechanical processes, and it has formed the (local) basis for the general relativistic theory of gravitation. In fact, no violation of local Lorentz invariance in any physical phenomenon has ever been detected, despite strenuous efforts.

Notice that for any incremental interval whose components are (dt,dx) with respect to one particular system of inertial coordinates, and (dt′,dx′) with respect to any other system of inertial coordinates, we have

This signifies that the quantity (dt)² - (dx)² is invariant with respect to all inertial coordinate systems. Since there exists a system of inertial coordinates with respect to which the spatial component dx is zero, it follows that the above invariant quantity is the square of the time differential dt along a path with respect to the rest frame of the path. This particular time differential is an invariant quantity, called the proper time of the interval (usually denoted by dτ to distinguish it from an arbitrary inertial time coordinate). It's easy to see that the inertial path between any two events has the maximum lapse of proper time. Any non-inertial path between those same two events will have a lesser lapse of proper time. In general, the lapse of proper time along the path of any physical entity corresponds precisely to the advance in the phase of the entity's quantum wave function. According to quantum mechanics, the wave function encodes everything knowable about a physical system, and there are no underlying structures or “hidden variables”, so the proper time along any interval actually is physical time.

When people first hear about special relativity they often wonder if it's necessary to think in terms of coordinate systems whose constant-t surfaces are skewed. They point out (correctly) that it's possible to construct a set of relatively moving coordinate systems that all share a common time coordinate. However, if two relatively moving systems of coordinates share a common time parameter, they cannot both be inertial coordinate systems, defined in the full sense of homogeneity and isotropy. This definition of an inertial coordinate system already imposes a specific set of constant-t surfaces for any given time axis in order to make inertia isotropic (i.e., the same in all spatial directions). We are certainly free to think in terms of non-inertial coordinate systems, but then we must be careful to remember that inertia is not isotropic with respect to such coordinate systems.

This highlights the problem with the incomplete way in which inertial coordinate systems are usually defined. As noted above, they are typically characterized simply as coordinate systems that are “not accelerated”, which is to say, coordinate systems in terms of which inertia is homogeneous. It’s vitally important to realize that being unaccelerated is a necessary but not a sufficient condition for a coordinate system to be inertial, because there exist coordinate systems with spatial axes oblique to the time axes (relative to the inertial orientation). In such systems, all inertial motion has uniform speed in a straight line, but nevertheless the coordinates are not (in general) inertial, because although Newton's first law of motion is satisfied, his second and third laws are not (even quasi-statically). In other words, inertia is not generally isotropic with respect to oblique coordinates. For any given time axis there is a unique orientation of the spatial axes compatible with inertial isotropy. This shows the significance of Einstein’s statement at the beginning of Part I of his 1905 paper on electrodynamics: “Let us take a system of coordinates in which the equations of Newtonian mechanics hold good.” It is significant that he does not limit this to just Newton’s first law. Of course, one result of Einstein’s paper is that Newton’s laws as traditionally formulated are valid only quasi-statically (as acknowledged by the footnote in Einstein’s paper), but the point is that he’s referring to systems of coordinates in terms of which inertia is not only homogeneous but also isotropic, because without isotropy Newton’s third law is not even quasi-statically valid.

Students are often told that Einstein and/or Poincare were the first to introduce operational definitions of simultaneity, but in fact there has always been an operational definition of simultaneity for inertial coordinates, because there is a unique simultaneity compatible with inertial isotropy for any given time axis. Galileo himself explained this in his "Dialogues on the Two Chief World Systems". What the discoveries of Bradley, Fizeau, Maxwell, Michelson, etc., made clear was that the propagation of electromagnetic disturbances is isotropic with respect to the same class of coordinate systems (the inertial coordinate systems) in terms of which mechanical inertia is isotropic.  In addition, they found that the value of k is not exactly zero (coincidentally at about the same time that Planck discovered that the value of h is not exactly zero), and consequently there is a finite invariant speed, equal to , for the set of inertial coordinate systems. From this we immediately have the concept of proper time, which is identified with the phase of the quantum wave function along any given timelike path. All the familiar consequence of special relativity follow.

Another common misconception is that we cannot assert the empirical isotropy of the one-way speed of light with respect to inertial coordinates. It’s actually quite possible to demonstrate this one-way isotropy. Simply observe that two identical particles acting on each other reach any given distance from their common center of mass coincident with two pulses of light emanating from that center. Obviously this does not demonstrate the one-way speed of either the particles or the light pulses, but it does demonstrate that if we define a system of coordinates such that mechanical inertia is isotropic (i.e., an inertial coordinate system), then the one-way speed of light is also isotropic with respect to that system of coordinates.

Return to MathPages Main Menu