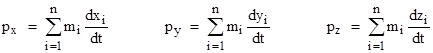What is an Inertial Coordinate System?

Arguably the single most important insight leading to the development of modern science was the recognition of a class of spatio-temporal coordinate systems in terms of which the motions of bodies satisfy (to high precision) a very simple set of mathematical relations, namely, Newton's laws of motion. The content of these laws consists of the assertion that for any isolated system of material particles the total “quantity of motion” (defined as mass times velocity) in any direction is conserved. In terms of a suitable system of space and time coordinates x,y,z,t this can be expressed by saying that the three quantities

for any isolated system of n particles are constant. If we consider a single isolated particle (meaning not subject to any external influence), this implies that the speed and direction of motion of any such particle is constant, which represents Newton’s “first law”. For two isolated particles, these equations imply that the rates of change of their individual momenta must be equal and opposite, which represents the combined empirical content of Newton’s second and third laws. Given one such “suitable” system of coordinates we can define infinitely many others by applying either a simple rotation or a “boost” transformation to the coordinates. (In Newton’s day a boost was considered to be a Galilean transformation, although today we would apply a Lorentz transformation.) These transformations are essentially defined to preserve “suitability”, i.e., they are defined such that in terms of the resulting coordinates the three quantities given above are constant for any isolated system of particles.

Newton's laws, as defined above, are obviously not valid in terms of arbitrary systems of coordinates. In order for those laws to be valid, the coordinates must be such that inertia is both homogeneous (the same at every place and time) and isotropic (the same in every direction). These requirements, together, are sufficient to fully determine the suitable coordinate systems (up to arbitrary scale factors), and since this definition is based on the properties of inertia, we may called such systems “inertial coordinate systems”. However, this term tends to be misleading, because although it is true that the coordinates themselves must be inertial, in the sense that any object whose position is stationary in terms of these coordinates must be in inertial motion (i.e., must be unaccelerated), this is not sufficient to ensure that all the conditions of an inertial coordinate system are satisfied. We must also require that, if an object’s spatial coordinates are linear functions of the time coordinate, then it is in inertial motion, which implies that the coordinate axes must be linear not only in time (i.e., unaccelerated) but also in space. These conditions are sufficient to ensure that Newton’s first law is satisfied, but they are still not sufficient to ensure that all three of Newton’s laws are formally satisfied in terms of these coordinates. So far we have only imposed the requirement of inertial homogeneity, but the coordinates must also satisfy the requirements of isotropy.

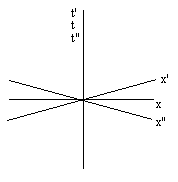
In order to fully specify the class of “suitable” coordinate systems in terms of which the laws of mechanics are valid, we must not only stipulate that the coordinates are defined such that free particles move at uniform speed in straight lines (i.e., Newton’s first law) , we must also impose a suitable definition of simultaneity at spatially separate points. Without this, Newton’s third law is not generally satisfied (not even approximately). This is a crucial aspect of the classical definition of what we may call “Newtonian coordinate systems”. To understand the significance of this condition, consider the figure below, which shows three different systems of space and time coordinates, denoted by (x,t), (x′,t′), and (x″,t″).

Any path that is a straight line with respect to one of these systems is a straight line with respect to all of them, so if one of them (say, x,t) is a Newtonian coordinate system, then Newton's first law (and arguably his second law) is satisfied with respect to each of these three coordinate systems. However, Newton's third law is not satisfied with respect to all of these coordinate systems. The transformation from (x,t) to (x′,t′) is of the form

for constants α, β, and ε. Hence any straight line x = at + b maps to the straight line

Now suppose identical particles initially resting at the common origin of (x,t) and (x′,t) exert a mutual impulse on each other, causing them to accelerate away from the spatial origin. According to Newton's third law, the net impulse exerted on these particles is equal in magnitude and opposite in direction, so they acquire the velocities v and –v with respect to the (presumed inertial) x,t coordinate system. (Note that this symmetrical impulse form of the third law is unambiguously applicable, even in a relativistic context). The paths of the two particles after the impulse are therefore described by the equations x = vt and x = –vt. Thus we have b = 0 and a = ±v, so the paths of the two particles with respect to the x',t' system are

In other words, when described in terms of the x′,t′ coordinate system, two identical particles initially at rest and exerting a mutual impulse on each other depart from the origin at speeds whose magnitudes are in the ratio (1 + εv) / (1 – εv), so Newton's third law (in combination with the second) is violated unless e equals zero.

This isn't just a minor detail. It is crucial for a meaningful understanding of reference frames and mechanics. The coordinate systems in terms of which the resistance to acceleration of a resting object is the same in all directions are not fully specified by the requirement to be unaccelerated, i.e., by the requirement to satisfy Newton's first law. The space and time components of a “Newtonian” inertial coordinate system must satisfy all three of Newton's laws, and this amounts to the imposition of an operational simultaneity. This aspect of inertial coordinate systems was clearly recognized at the very beginnings of the modern science of dynamics in the writings of Galileo, who wrote (in "Dialogue on the Two Chief World Systems") about leaping in different directions on the deck of a moving ship, noting that with equal force we will reach equal distances (implicitly in equal times), regardless of the direction. This essentially expresses Newton's third law and the conservation of momentum, which necessarily entails a specific operational definition of simultaneity, namely, inertial simultaneity. Unfortunately, this early insight seems to have been mostly forgotten by around 1900, when Poincare and Einstein were credited as the first to suggest the need for an operational definition of simultaneity. In truth the operational definition of simultaneity entailed by Newton’s third law had already been in use for over two centuries. The real contribution of physicists in the early 1900's was to recognize that electromagnetic simultaneity (i.e., synchronization based on light signals) and inertial simultaneity (i.e., synchronization based on mechanical inertial isotropy) are identical, thereby making it feasible to unify mechanics and electromagnetism within a single relativistic framework.

Given the convoluted history of the subject, it is perhaps not surprising that there is very widespread confusion in the literature (at all levels) as to the necessary and sufficient conditions for the laws of mechanics to be satisfied in terms of a given system of coordinates. This confusion can be seen even in the unusually thoughtful presentation in E. T. Whittaker’s historical introduction to relativity:

According to Newton's First Law of Motion, any particle which is free from the action of impressed forces moves, if it moves at all, with uniform velocity in a straight line…We can assert as a fact of experience that certain systems of axes exist such that free particles move in straight lines with reference to them. Moreover, we can assert that there exist certain ways of measuring time such that the velocity of free particles along their rectilinear paths is uniform. A set of axes in space and a system of time-measurement, which possess these properties, may be called an inertial system of reference…. In Newtonian mechanics, if S is an inertial system of reference, and if S' is another system such that the axes of S' have any uniform motion of pure translation with respect to the axes of S, and if the system of time-measurement is the same in the two cases, then S' is also an inertial System of reference: the Newtonian laws of motion are valid with respect to S' just as with respect to S.

The problem here – as in almost the entire literature on this subject – is the invalid extrapolation from Newton’s first law to all of Newton’s laws. Whittaker correctly notes that the first law is satisfied only in terms of space and time coordinates that are not accelerating, but then he jumps to the assertion that the Newtonian laws (plural) of motion are valid with respect to these same systems – an assertion that is patently false. Compatibility with Newton’s first law is not sufficient to ensure compatibility with the second and third laws. To cement the confusion, the phrase “inertial coordinate system” is commonly used interchangeably to refer to (1) coordinate systems compatible with Newton’s first law, and (2) coordinates systems compatible with all three of Newton’s laws, despite the fact that the latter are only a subset of the former. There ought to be two different terms for these distinct sets of coordinate systems, but unfortunately a single term is used for both.

A further source of confusion when attempting to unravel the overlapping definitions is due to the fact that Newton’s second and third laws, in their usual formulations, entail not just the essential symmetries of inertia but also, implicitly, the assumption that relatively moving systems of fully symmetrical coordinate systems are related by Galilean transformations, an assumption now known to be false. Therefore, we need to extract the essence of Newton’s three laws and separate them from assumptions about coordinate transformations. The factual essence of the Newtonian and Galilean concept of inertia is that there exists a system of space and time coordinates in terms of which mechanical inertial is both homogeneous and isotropic. Homogeneity corresponds to the fact that free objects move uniformly in straight lines (i.e., Newton’s first law), and isotropy corresponds to the fact that two identical resting objects acting against each other acquire equal and opposite speeds in equal times (representing the factual content of Newton’s second and third laws). By rights such coordinate systems deserve the name “inertial”, because they are the unique coordinate systems in terms of which inertia is maximally symmetrical, but unfortunately the word “inertial” carries connotations from its use as an adjective for material objects. A material object possesses only an individual world-line within spacetime, and the object may be called “inertial” if its space coordinates are linear functions of the time coordinate. In other words, an object is inertial if and only if it is unaccelerated. In contrast, a system of coordinates is much more extensive than a single worldline, and is not fully specified merely by requiring the absence of acceleration. Coordinate systems can be defined in infinitely many ways, but if we are to define our coordinate system in terms of inertia, we need to stipulate not only the homogeneity but also the isotropy of inertia. Without both of these requirements, the coordinate system is under-specified. Hence the term “inertial” when applied to coordinate systems means more than just that free objects are unaccelerated, it means that the resistance to acceleration of a resting body is the same in all spatial directions.

Despite this, the most common definition of the term “inertial coordinate system” appearing in the literature is simply a coordinate system compatible with Newton’s first law. It is, of course, permissible to define the term “inertial coordinate system” in this way, but then we must recognize that (1) the systems so defined are not fully specified, and (2) inertia is not generally isotropic in terms of coordinate systems that satisfy only this partial definition. Unfortunately, almost every published reference on the subject (at all levels) not only defines inertial coordinate systems purely in terms of Newton’s first law, they then immediately assume these coordinate systems are thereby fully defined (which they aren’t) and that Newton’s second and third laws hold good in terms of these coordinates (which they don’t).

Considering the central importance of Newtonian inertial coordinate systems (and the equivalence classes known as inertial reference frames), it’s unfortunate that nearly all modern textbooks give seriously deficient definitions of inertial coordinate systems. From a large sampling of texts at all levels, it appears that every one of them claims that a necessary and sufficient condition for a reference frame to be inertial is simply that it is unaccelerated, and then they go on to claim that all of Newton’s laws (or their relativistic counterparts) are valid in terms of these coordinate systems. A coordinate system is compatible with Newton’s laws, they say, if and only if, with respect to that system, every object not subject to an external force moves at uniform speed in a straight line. As explained above, this is false. Satisfaction of Newton's first law of motion is not sufficient to define an inertial coordinate system – if, by “inertial coordinate system” we mean a system of space and time coordinates in terms of which the laws of mechanics are formally valid. Sometimes these texts invoke the second law instead of the first, but they are used for the same purpose, i.e., simply to establish that the reference frame is unaccelerated. The formal definition of inertial reference frames given in every one of these sources fails to require that the third law be satisfied, despite the fundamental importance of this requirement.

Needless to say, we can define terms any way we like, and it would be permissible to define the phrase “inertial coordinate system” as simply a characterization of a large class of coordinate systems, a small subset of which are fully compatible with the laws of mechanics, but this cannot be what the text books are doing, because they immediately assert that their definition based solely on Newton’s first law is sufficient to ensure compatibility with all the laws of mechanics, which is clearly false. So either they are defining the term “inertial coordinate system” incorrectly, or they are incorrectly describing the properties of those systems. It seems most reasonable to reserve the expression “inertial coordinate system” to those systems of space and time coordinates in terms of which inertia is homogeneous and isotropic, because this is sufficient to unambiguously define a unique reference frame for each state of motion. On this basis, the definition of inertial coordinate systems given in all existing modern text books (at least all I have seen) is wrong. (I restrict this to “modern” texts, because clearly Galileo, Newton, and the other 17th century originators of modern physics understood the need for inertial isotropy, but this understanding seems to have been lost in the intervening centuries. If it had not been forgotten, scientists would never have regarded the concept of an operational definition of simultaneity to be novel when it was re-introduced by Poincare and Einstein.)

As a typical example of the (deficient) definition of inertial reference frames, here is how the standard college text, Physics, by Halliday and Resnik defines them:

...it is possible to find a family of reference frames in which a particle [free of applied forces] has no acceleration. The fact that bodies stay at rest or retain their uniform linear motion in the absence of applied forces is often described by assigning a property to matter called inertia. Newton's first law is often called the law of inertia and the reference frames to which it applies are called inertial frames. ...an inertial frame... is a reference frame that is either at rest or is moving at constant velocity with respect to the average positions of the fixed stars; it is the set of reference frames defined by Newton's first law, namely, that set of frames in which a body will not be accelerated if there are no identifiable force-producing bodies in its environment.

As mentioned previously, it is permissible to define “inertial frame” in this limited sense, but unfortunately Halliday and Resnik go on to assert that all three of Newton’s laws are (approximately) valid in terms of inertial frames, an assertion that would be true only if we define “inertial frame” in the full sense, stipulating isotropy as well as homogeneity. Of course, this reduces all of Newton’s laws to tautologies, albeit extraordinarily useful ones. They essentially amount to the definition of Newtonian inertial coordinate systems, and the usefulness of this definition arises from the fact that such coordinate systems actually exist.

By the way, in addition to the deficiency of Halliday and Resnik’s definition due to its failure to invoke the third law, we should mention that the phrase "observations made from an inertial frame" is pedagogically awful. Such statements have no real meaning, and serve only to mislead and confuse students, because everything is "in" an inertial frame. In fact, everything is in infinitely many inertial frames, so to talk about making observations "from" an inertial frame is sloppy at best, and at worst it's indicative of a real lack of clarity in understanding. The same type of awful terminology appears throughout the literature, even in books on the theory of relativity, where it is crucially important to be clear and precise about the meaning of statements made in terms of specific systems of reference.

In any case, Halliday and Resnik are not alone in presenting an erroneous definition of the reference systems in terms of which Newton’s laws are formally valid. To substantiate the claim that the failure to invoke Newton's third law in the definition of inertial reference frames is widespread, consider the following summary of the definitions given in several well-known texts:

A reference frame is said to be inertial when... every test particle that is initially at rest, and every test particle that is initially in motion, continues that motion without change in speed or in direction. [Spacetime Physics, Taylor and Wheeler]

...in order not to introduce effects due to the acceleration of the observer, we must take care to apply [the second law] in a frame that is itself unaccelerated. We refer to these as inertial frames. In many situations, one can often effectively assume that an inertial frame of reference is one at rest with respect to the earth. [Philosophical Concepts in Physics, Cushing]

...let us assume that we have found an inertial reference frame, and therefore that Newton's laws apply for motions relative to this frame. It can be shown that any other reference frame that is not rotating but is translating with uniform velocity relative to an inertial frame is itself an inertial frame... For example, if system B is translating with constant velocity with respect to an inertial system A, then... observers on systems A and B see identical forces, masses, and accelerations, and therefore [the second law] is equally valid for each observer. [Principles of Dynamics, Greenwood]

In order to fix an event in space, an observer may choose a convenient origin in space together with a set of three Cartesian coordinate axes. We shall refer to an observer's clock, ruler, and coordinate axes as a frame of reference... there exists a privileged set of bodies, namely those not acted on by forces. The frame of reference of a co-moving observer is called an inertial frame. [Introducing Einstein's Relativity, D'Inverno]

The reference frame attached to a [free-falling] spacecraft simulates an inertial reference frame: a test particle at rest relative to the spacecraft remains at rest, a test particle in motion remains in motion with uniform velocity. [Gravitation and Spacetime, Ohanian and Ruffini]

Inertial reference frame, defined by uniform velocity of free test particles... [Gravitation, Misner, Thorne, and Wheeler]

Newton's first law serves as a test to single out inertial frames among rigid frames: a rigid frame is called inertial is free particles move without acceleration relative to it. [Essential Relativity, Rindler]

A conceptual framework, rigidly connected with some material body or other well-defined point, is often called a frame of reference… among all the frames of reference conceivable, there exists a set of frames with respect to which the law of inertia takes its familiar form: In the absence of forces, the space coordinates of a mass point are linear functions of the time. These frames of reference are called inertial frames. It was found that all of the laws of mechanics take the same form when stated in terms of any one of these inertial systems… [Introduction to the Theory of Relativity, P. G. Bergmann]

This list could be extended indefinitely. Essentially every text book perpetuates this fundamental error by defining inertial coordinate systems (and frames) only using Newton’s first law, and then subsequently assuming inertia is isotropic in terms of those coordinate systems – an assumption which is generally false. Appeals to notion of a “rigid framework” in these texts may have been thought to connote some sense of simultaneity, but of course only a perfectly rigid structure could accomplish this, and no such structure can exist. The most we can have is a static configuration in equilibrium, but the mere existence of an equilibrium configuration of entities does not single out any particular correspondence between the time coordinates assigned to those various structure. When Poincare and Einstein began to speak explicitly about the need for an operational definition of simultaneity, many physicists regarded it as a novel idea, but only because they had forgotten that ever since Galileo the definition of simultaneity implicit in Newtonian mechanics had always been operationally based on the isotropy of inertia, which is contained in the complete definition of Newtonian inertial coordinate systems.

Oddly enough, some of the modern textbook definitions seem to have been carried over from one text to another. For example, Taylor and Wheeler introduce their formal definition (quoted above) by discussing at length a spaceship in free-fall. They say "we call such a space ship that rises and falls freely an inertial reference frame...", and then they go on to talk about the motions of "test particles", terms and images that reappear almost verbatim in Ohanian and Ruffini. (The first endorsement on the book cover of the latter is from Wheeler, who wryly comments that it is the best gravitation book on the market "of 500 pages or less". Wheeler's own Gravitation is over 1200 pages.) To their credit, Ohanian and Ruffini do refrain from repeating the ridiculous statement that a space ship is an inertial reference frame (is it any wonder that students presented with such statements becomes confused, and begin to talk in terms of measurements performed in an inertial reference frame?), but they carry over the fundamentally deficient definition, failing to ever mention the necessity of imposing Newton's third law in order to give a complete definition of Newtonian inertial coordinates, and never acknowledging the crucial fact that this represents the imposition of a definite operational simultaneity. This illustrates how difficult it is – even professional scientists who, on some level, must surely know better – to free our minds from the Galilean assumption of absolute simultaneity.

Another source of confusion over the definition of inertial coordinate systems arises when we consider curvilinear coordinates. In this regard the confusion is not universal, but still very prevalent, especially in introductory texts (where it is arguably most important to be clear). One way of expressing Newton’s second law is that the acceleration of a particle equals the net force (per unit mass) applied to the particle, but the meaning of acceleration is ambiguous without further specification. We might identify it with the second derivative of the particle’s space coordinates with respect to the time coordinate, but this corresponds to the true acceleration in the Newtonian sense only for certain systems of coordinates. Most texts acknowledge that this correspondence fails with respect to accelerating systems of coordinates, but they overlook the fact that it also fails with respect to curvilinear space coordinates. Of course, it’s possible to include terms in the equations of motion (in addition to the basic second derivative) to compensate for curvilinear space coordinates, but it is equally possible to compensate for curved time coordinates (i.e., acceleration). In both cases we are simply dealing with systems of coordinates whose time and/or space axes are curves relative to inertial worldlines. From this point of view, a system of stationary polar coordinates (for example) is not an inertial system, just as a rotating system of rectangular coordinates is not an inertial system. In both cases, inertial worldlines are cannot be characterized by spatial coordinates that are linear functions of the time coordinate.

Some of the confusion in the literature regarding this point is simply due to careless quotations taken out of context. For example, one widely accessible reference begins its discussion of “inertial reference frames” by quoting from the first paragraph of Einstein’s 1916 paper on general relativity, in which he briefly recounts the foundations of special relativity.

If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K' moving in uniform translation relatively to K.

From this one might conclude that Einstein was claiming that “physical laws hold good in their simplest form” in unaccelerated polar coordinate systems (for example) just as they do in rectangular coordinate systems. But this overlooks the context in which Einstein’s comment was made. In composing a research article for professional physicists, one does not always go back and review every elementary consideration. Einstein took for granted that the meaning of “system of coordinates” in which physical laws hold good in their simplest form would be understood as referring to rectangular coordinates. This was described quite explicitly in Einstein’s 1905 paper on special relativity, where he defines two systems of inertial coordinates K and k as follows:

Let us in stationary space take two systems of coordinates, i.e., two systems each of three rigid material lines, perpendicular to one another and issuing from a point…

Thus in this context he is using the term “system of coordinates” as synonymous with rectangular coordinates, i.e., coordinates whose axes are perpendicular straight lines. This convention simplifies the discussion of special relativity, but it should not be taken to suggest that every proposition about unaccelerated rectangular coordinate systems also applies to unaccelerated systems with curvilinear spatial coordinates. Clearly the Newtonian (or special relativistic) laws of mechanics do not take their simplest form when expressed in terms of stationary curved spatial coordinates, so in that sense they are not Newtonian coordinate systems, despite being unaccelerated.

Still another source of confusion is the concept of a reference frame, whose common definitions are based on the false presumption of absolute simultaneity among systems of inertial coordinates. The only meaningful definition of a reference frame is that it consists of an equivalence class of mutually stationary coordinate systems. On this basis a reference frame includes coordinate systems with both rectangular and curvilinear spatial coordinates, and yet (as noted above) the laws of mechanics do not take the same form in terms of all these systems. Again, the fact that it’s possible to compensate for curvilinear coordinates by including extra terms in the equations of motion does not imply that they should be considered as Newtonian inertial coordinate systems, because we can just as well compensate for curvilinear time axes (i.e., acceleration), and yet we don’t conclude that these constitute inertial coordinate systems. Perhaps the most relevant quotation from Einstein on this subject is from his 1949 autobiographical notes, in which he described how in 1908 he had realized that it was necessary to extend the special theory of relativity to accommodate nonlinear coordinate transformations (of space as well as time):

Why were another seven years required for the construction of the general theory of relativity? The main reason lies in the fact that it is not so easy to free oneself from the idea that coordinates must have a direct metrical significance.

Return to MathPages Main Menu