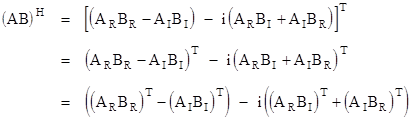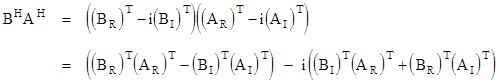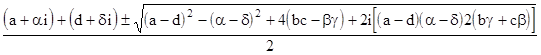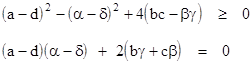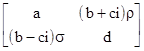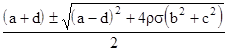Hermitian Matrices

Given a matrix A of dimension m x k (where m denotes the number of rows and k denotes the number of columns) and a matrix B of dimension k x n, the matrix product AB is defined as the m x n matrix with the components

for μ ranging from 1 to m and for ν ranging from 1 to n. Notice that matrix multiplication is not generally commutative, i.e., the product AB is not generally equal to the product BA.

The transpose A^T of the matrix A is defined as the k x m matrix with the components

for μ ranging from 1 to m and for κ ranging from 1 to k. Notice that transposition is distributive, i.e., we have (A+B)^T = (A^T + B^T).

Combining the preceding definitions, the transpose of the matrix product AB has the components

Hence we've shown that

We can also define the complex conjugate A^* of the matrix A as the m x k matrix with the components

Notice that the matrix A can be written as the sum A_R + iA_I where A_R and A_I are real valued matrices. The complex conjugate of A can then be written in the form

We also note that transposition and complex conjugation are commutative, i.e., we have (A^T)^* = (A^*)^T. Hence the composition of these two operations (in either order) gives the same result, called the Hermitian conjugate (named for the French mathematician Charles Hermite, 1822-1901) and denoted by A^H. We can express the components of A^H as follows

A Hermitian matrix is defined as a matrix that is equal to its Hermitian conjugate. In other words, the matrix A is Hermitian if and only if A = A^H. Obviously a Hermitian matrix must be square, i.e., it must have dimension m ´ m for some integer m.

The Hermitian conjugate of a general matrix product satisfies an identity similar to (1). To prove this, we begin by writing the product AB in the form

Thus the Hermitian conjugate can be written as

Applying identity (1) to the transposed products, we have

We recognize the right hand side as the product of the Hermitian conjugates of B and A, i.e.,

Consequently we have the identity

We're now in a position to prove an interesting property of Hermitian matrices, namely, that their eigenvalues are necessarily real. Recall that the scalar λ is an eigenvalue of the (square) matrix A if and only if there is a column vector X such that

Taking the Hermitian conjugate of both sides, applying identity (2), and noting that multiplication by a scalar is commutative, we have

Now, if A is Hermitian, we have (by definition) A^H = A, so this becomes

If we multiply X by both sides of this equation, and if we multiply both sides of the original eigenvalue equation by XH, we get

Since the left hand sides are equal, and since multiplication by a scalar is commutative, we have λ = λ^*, and therefore λ is purely real.

Of course, the converse is not true. A matrix with real eigenvalues is not necessarily Hermitian. This is easily seen by examining the general 2 x 2 matrix

The roots of the characteristic polynomial

are

The necessary and sufficient condition for the roots to be purely real is that both of the following relations are satisfied

If the matrix is Hermitian we have α = δ = 0, b = c, and β = –γ, in which case the left hand expression reduces to a sum of squares (necessarily non-negative) and the right hand expression vanishes. However, it is also possible for these two relations to be satisfied even if the original matrix is not Hermitian. For example, the matrix

is not Hermitian if ρ ≠ σ, but it has the eigenvalues

which are purely real provided only that ρσ ≥ 0.

Returning to Hermitian matrices, we can also show that they possess another very interesting property, namely, that their eigenvectors are mutually orthogonal (assuming distinct eigenvalues) in a sense to be defined below. To prove this, let λ₁ and λ₂ denote two distinct eigenvalues of the Hermitian matrix A with the corresponding eigenvectors X₁ and X₂. (These subscripts signify vector designations, not component indices.) Then we have

Taking the Hermitian conjugate of both sides of the left hand equation, replacing A^H with A, noting that λ₁^* = λ₁, and multiplying X₂ by both sides gives

Now we multiply both sides of the right hand equation by X₁^H to give

The left hand sides of these last two equations are identical, so subtracting one from the other gives

Since the eigenvalues are distinct, this implies

which shows that the "dot product" of X₂ with the complex conjugate of X₁ vanishes. In general this inner product can be applied to arbitrary vectors, and we sometimes use the bra/ket notation introduced by Paul Dirac

where, as always, the asterisk superscript signifies the complex conjugate. (The subscripts denote component indices.) Terms of this form are a suitable "squared norm" for the same reason that the squared norm of an individual complex number z = a + bi is not z², but rather z*z = a² + b².

Hermitian matrices have found an important application in modern physics, as the representations of measurement operators in Heisenberg's version of quantum mechanics. To each observable parameter of a physical system there corresponds a Hermitian matrix whose eigenvalues are the possible values that can result from a measurement of that parameter, and whose eigenvectors are the corresponding states of the system following a measurement. Since a measurement yields precisely one real value and leaves the system in precisely one of a set of mutually exclusive (i.e., "orthogonal") states, it's natural that the measurement values should correspond to the eigenvalues of Hermitian matrices, and the resulting states should be the eigenvectors.

Return to MathPages Main Menu