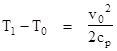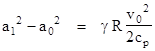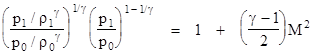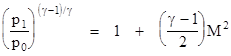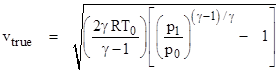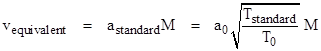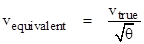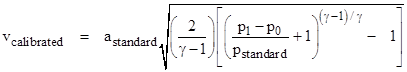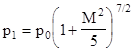True, Equivalent, and Calibrated Airspeeds

The energy equation for adiabatic flow of an ideal gas is

where v is the flow velocity and h is the specific enthalpy. This implies that if a flow with free stream velocity v₀ and enthalpy h₀ is brought to rest adiabatically, and if h₁ is the enthalpy of the resting gas, then

Also, for an ideal gas we have dh/dT = c_p, where the specific heat c_p is essentially constant for relatively small changes in temperature, so this equation can be written as

Now, the speed of sound in an ideal gas is given by where γ = c_p/c_v is the ratio of specific heats and R is the gas constant, so we can express any given temperature T in terms of the speed of sound at that temperature. With these substitutions, the preceding equation becomes

Also, for an ideal we have R = c_p c_v, so we can make this substitution, divide through by a₀², and re-arrange terms to give

The ratio v₀/a₀ is, by definition, the Mach number M of the free stream, and since temperature is proportional to the square of the speed of sound, the ratio (a₁/a₀)² equals the ratio of temperatures T₁/T₀. Hence we have

Furthermore, using the ideal gas equation p = ρRT we can substitute for the temperatures to give

As discussed in The Speed of Sound, for an adiabatic quasi-static (i.e., isentropic) process, the ratio p/ρ^γ is constant. Thus if we re-write the above equation as

the first factor on the left side is unity, and we arrive at the formula for the isentropic pressure rise of an ideal fluid being brought to a stop from a Mach number M

Solving this equation for M and then multiplying through by the freestream speed of sound , we have the formula for the true airspeed v_true = v₀ as a function of the freestream static pressure p₀, the total (stagnation) pressure p₁, and the freestream static temperature T₀

In some primitive systems, only the quantity called dynamic pressure was measured. For incompressible fluids this quantity is

For convenience we can define a quantity called equivalent airspeed to be the airspeed that would exist with sea level ISA density ρ^* rather than the actual density at the given flight condition. Thus we have

So, recalling that p = ρRT, we have

Where T* = 518.67 R and p* = 14.696 psia, and we define and θ = T₀/T^*, and δ = p₀/p^*. For reference, we also note the speed of sound at sea level standard day conditions:

a_standard = √(γRT^*) = 1116 ft/sec = 661.47 knots

With certain kinds of primitive instrumentation systems we can measure only the difference p₁ p₀ between the total and static pressures. This difference is sometimes called the impact pressure, which is the same as the dynamic pressure (1/2)ρv² for incompressible flow, but not for compressible flow. Even if we can re-write the ratio p₁/p₀ as (p₁ p₀)/p₀ + 1, we would still need to know the static pressure p₀ (in addition to the impact pressure) in order to compute equivalent airspeed. However, lacking the static pressure, we can agree by convention to simply use the standard sea level static pressure p^* in place of p₀. When this is done, we get the following formula for calibrated airspeed as a function only of the impact pressure

where p_standard = 14.696 psia. Given the definition of calibrated airspeed, we sometimes need to compute it based on the actual measured values of the static pressure p₀ and freestream Mach number M. (Of course, knowing p₀ and M, we could compute equivalent airspeed, but convention may still force us to deal with calibrated airspeed.) For convenience, we will set γ = 1.4, which is the value for atmospheric air. Then p₁ is given in terms of p₀ and Mach by the relation

Substituting this into the calibrated airspeed equation gives

where δ denotes the pressure ratio p₀/p_standard. For values of M less than this can be expanded into a convergent power series in M, the first few terms of which are

In terms of the true airspeed this is

For small Mach numbers (much less than 1) the zeroth order term of the expansion is often accurate enough for practical purposes, but for Mach numbers approaching 1 it is necessary to take account of the higher-order terms or else simply use the exact analytical expression.

Return to MathPages Main Menu