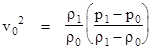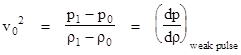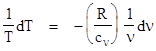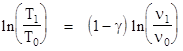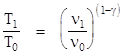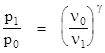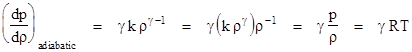The Speed of Sound

The first analytical determination of the speed of sound was given by Isaac Newton in Proposition 49 of Book II of the Principia. For sea level air at a typical ambient temperature he computed a value of 979 ft/sec, which is too low by about 15%, the true value being about 1116 ft/sec. To account for this difference, Newton suggested various non-ideal effects, although it remained for Laplace to rectify the deficiency in Newton's analysis. Nevertheless, the basic method conceived by Newton was essentially correct, and Laplace was surely correct in saying that the analysis is "a monument to Newton's genius" (especially considering that it was just one of many incidental results contained in the Principia).

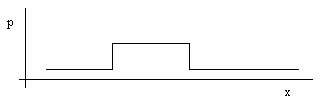
To determine the speed at which a plane pressure disturbance propagates through an elastic medium, consider a single "square" pulse of elevated pressure (and density) as shown below.

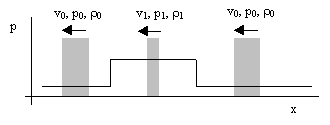
We could suppose that this pulse is moving to the right at some speed v₀, but for convenience let us choose a coordinate system co-moving with the pulse, so that the pulse is stationary and the medium is moving to the left. The figure below shows three slices of equal mass, one of them is just approaching the pulse, another is inside the pulse, and the third has passed through the pulse. Since the density is higher inside the pulse, continuity of the flow requires that the velocity of the medium inside the pulse must be lower than the velocity outside the pulse.

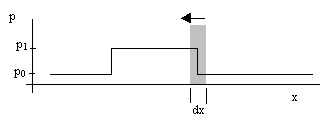
This implies that the medium must decelerate as it enters the pulse, and then accelerate as it leaves the pulse. Now focus on an incremental slice of the medium just entering the region of elevated pressure and density as shown below.

The leading surface of this slice is inside the pulse, so it is subjected to the pressure p₁, whereas the trailing surface is still subject to the outside pressure p₀. Hence there is a net force (per unit area) on this slice equal to p₁ – p₀ in the rightward direction, i.e., tending to decelerate the medium. This force is applied for a length of time dt, which is the time required for the slice of thickness dx to cross the boundary. Since the outside medium is moving at the speed v₀, we have dt = dx/v₀. Applying Newton's second law in the form F = ma to this slice, we note that the decelerating force per unit area is p₁ – p₀, the mass per unit area is ρ₀dx, and the acceleration is a = (v₀ – v₁)/dt, so we have

Replacing the duration dt with dx/v₀, this becomes

Continuity of flow (per unit area) requires that the product of density and velocity is constant, so we have ρ₀v₀ = ρ₁v₁, and we can subtract ρ₁v₀ from both sides of this equality to give the relation

Eliminating the term v₀ - v₁ from the two preceding equations, and rearranging, we have

In the limit as the magnitude of the pressure disturbance approaches zero (which is appropriate because acoustical waves normally consist only of extremely weak pressure differences), the ratio of absolute densities ρ₁/ρ₀ approaches 1, so we have Newton's basic result for the propagation speed v₀ of an acoustic disturbance in an elastic medium

This shows that the speed of sound in any given medium depends on how the density varies with pressure (and vice versa). Incidentally, the "bulk modulus" of an elastic substance is defined as K = ρ(dp/dρ), so the speed of sound in a medium with bulk modulus K can be written as .

At this point, in order to determine the speed of sound in air (or any other ideal gas), we need to know how the pressure and density are related. Newton was aware of Boyle's Law, which states that, at constant temperature, the density of a gas is proportional to the pressure. We would express this in the form of the ideal gas law p = ρRT, where R is the gas constant, and from this we have dp/dρ = RT at constant temperature. Inserting this into the equation for the speed of sound would give , and this is essentially the basis of Newton's original numerical estimate for the speed of sound in air. He assessed the quantity "RT" empirically, but taking the modern value of the gas constant R for air

R  =  1716  (ft·lb_f)/(slug×deg R)  =  1716  (ft/sec)² / (deg R)

and assuming the standard day ambient temperature at sea level of T = 518.7 deg R, this gives an estimate of about 943 ft/sec, which is fairly close to Newton's calculated value of 979 ft/sec (and remember that Newton was shading the numbers as high as possible, knowing that the experimental speed of sound was near 1100 ft/sec).

The flaw in this reasoning is the assumption that changes in pressure of an acoustic disturbance are exactly proportional to the changes in density. This proportionality would hold if the temperature was constant, but in fact the temperature is not constant across an acoustic disturbance. In regions where the pressure and density increase, the temperature also increases slightly. (There is not nearly enough time for heat flow to equalize the dynamic variations in temperature.) Hence we cannot treat T as a constant, so we cannot simply differentiate the ideal gas law to give dp/dρ = RT.

To determine the correct derivative we need to recall some basic thermodynamics. The specific volume ν is the inverse of the density ρ, so the ideal gas law can be written in the form pν = RT. Also, recall that the specific (i.e., per pound) internal energy u of an ideal gas is strictly a function of temperature, so the specific heat c_ν = (∂u/∂T)_ν equals the total derivative du/dT. Likewise the specific enthalpy h = u + pν of an ideal gas is strictly a function of temperature, so the specific heat c_p = (∂h/∂T)_p equals the total derivative dh/dT. Furthermore, since pν = RT for an ideal gas, we can write the enthalpy as h = u + RT, and the differentials are then related by dh = du + RdT. Dividing through by dT, we have the important relation c_p – c_ν = R for an ideal gas.

Now, if we rapidly make an incremental change dν to the specific volume of a given quantity of an ideal gas (rapidly enough that there is no time for significant heat transfer), the incremental change du in the internal energy equals the work done by the boundary, i.e., du = –pdν. This is called an adiabatic change, meaning that the only energy transfer is in the form of work, not heat flow. (We are also assuming the changes are slow enough that the medium is always approximately in thermodynamic equilibrium, i.e., we assume the processes are quasi-static.) Making the substitutions du = c_νdT and p = RT/ν and re-arranging, this energy equation can be written as

Also, since R = c_p – c_ν , we can write the quantity in parentheses as γ - 1, where γ = c_p/c_ν is the ratio of specific heats. This ratio is found to be essentially constant for a given substance over a fairly wide range of temperatures. For example, the ratio of specific heats for air can be taken as γ = 1.4 for most purposes. Integrating the above equation from T₀,ν₀ to T₁,ν₁ gives

Exponentiating both sides, we have the adiabatic relation for the temperature and specific volume of an idea gas

Making the ideal gas substitutions p₀ν₀/R and p₁ν₁/R for the temperatures T₀ and T₁ we get

Since the specific volume ν is the inverse of the density ρ, this relation shows that the ratio p/ρ^γ is constant during a quasi-static adiabatic process. Hence for some constant k we have p = kρ^γ, which gives the derivative

This is the appropriate derivative to use for acoustic disturbances in an ideal gas, so substituting this into Newton's basic equation gives the correct propagation speed for sound in an ideal gas

This differs from the isothermal formula by a factor of , and since γ = 1.4 for air, the effect is to increase the isothermal estimate by a factor of 1.1832..., which gives 1115.7 ft/sec for the speed of sound in air at the standard sea level ambient temperature (59 F).

For a more sophisticated approach to deriving the propagation speed of acoustic waves, return to a "stationary" coordinate system in which the medium is nominally at rest, and write the complete continuity equation (per unit area) in differential form

The left hand term signifies the change of mass flow with position, and the right hand term represent the time rate of change of density at each position. In words, this equation says that the difference between the mass flow rate into a small region and the mass flow rate out of that region equals the rate of accumulation within that region.

The full momentum equation is

This is essentially just an expression of "F=ma" for an incremental slice of the medium. The left hand term represents the net force on the slice at a given instant, and the right side of the equation represents the acceleration of the mass density ρ. There are two terms inside the parentheses because in general the velocity is a function v(t,x) of both time and position, and the acceleration is the total derivative of v. The total differential dv is given by

Dividing through by dt, and noting the dx/dt = v, we find that the total acceleration dv/dt is indeed the quantity inside the parentheses of the momentum equation. Also, since the pressure is a function p(ρ) of the density, we can write the force term as

where we have defined the constant . So, to collect our results so far, and write them in more convenient form, the continuity and momentum equations are

These equations are non-linear, but remember that the medium is nominally at rest with respect to these coordinates, so the speed v is very near zero, with just relatively slight perturbations to propagate the disturbance. On this basis, the terms with the coefficient v can be neglected, and the two equations of motion take the simplified form

If we define the condensation as σ = ln(ρ), then these equations can be simplified still further

Taking the partial derivative of the left hand equation with respect to t, and of the right hand equation with respect to x, we have

Since partial differentiation is commutative, the difference between these two equations gives

which of course is the one-dimensional wave equation with a propagation speed of c. Likewise if we take the partial derivative of the earlier left hand equation with respect to x, and of the right hand equation with respect to t, and multiply through the former by c², the difference between the two resulting equations is

Hence, both the condensation σ (i.e., the natural log of the density) and the velocity v of the medium satisfy the wave equation with the characteristic speed .

Return to MathPages Main Menu