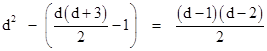Cramer's Paradox

An algebraic plane curve is a locus of points with orthogonal coordinates x,y such that C(x,y) = 0 where C is a polynomial with constant complex coefficients. The degree of a curve is the highest sum of the powers of x and y appearing in any single term of the polynomial. For example, the curve corresponding to x⁴y³ − 9x²y + 3xy² − 5 = 0 is of degree 7. The most general polynomial of degree d consists of terms of the form c_ijxⁱy^j for non-negative integers i,j with i + j ≤ d. There is just a single term with i + j = 0, and two terms with i + j = 1, and three terms with i + j = 2, and so on. Therefore the general polynomial of degree d consists of 1 + 2 + ... + d + (d+1) = (d+1)(d+2)/2 terms, each with an independent coefficient. However, equating this polynomial to zero, we can divide through by any one of the (non-zero) coefficients, thereby reducing the number of arbitrary coefficients by one. Thus we have (d+1)(d+2)/2 − 1 = d(d+3)/2 free coefficients.

Given d(d+3)/2 arbitrarily selected points on the plane, we can insert the coordinates of these points into the polynomial C(x,y) = 0 to give d(d+3)/2 linear equations in the same number of unknown coefficients, so we can solve for those coefficients to give the unique polynomial of degree d passing through those d(d+3)/2 points. However, this presents something of a paradox if we recall Bezout's Theorem, which states that two algebraic curves of degree m and n intersect in exactly mn points (counting complex intersections, multiplicities, and points at infinity). Thus two curves of degree d intersect in d² points. For d = 1 (straight lines) it follows that there is a unique curve passing through any two given points, and two curves of degree one intersect in just one point. For d = 2 (conics) there is a unique curve passing through any five points, and two curves of degree two intersect in four points. These cases are not surprising, but when we proceed to the case d = 3 (cubics) we find that there is a unique curve of degree three passing through any nine given points, and any two cubic curves intersect in nine points. Here we see a contradiction, because there are at least two distinct cubics passing through a set of nine points, even though nine points supposedly determine a unique cubic. The paradox becomes even more acute for higher degrees, such as d = 4 (quartics). There is a unique quartic passing through any 14 given points, and yet any two quartics intersect in 16 points. This apparent contradiction is known as Cramer's paradox, after Gabriel Cramer, although it was first mentioned by Colin MacLaurin.

A resolution of the paradox was given by Cramer, and later expanded and clarified by Julius Plucker. Let's take the case of two quartics, i.e., curves of degree d = 4. To understand the paradox it's useful to note that while 14 points determine a quartic, 13 points determine a one-parameter family of quartics, each of which passes through the 13 given points. Let C₁(x,y) = 0 and C₂(x,y) = 0 signify two distinct such quartics. It follows that C₁ + μC₂ = 0 is another such quartic for any complex number μ. The crucial realization is that this one-parameter family of quartics represents all the quartics that pass through the 13 given points. To prove this, suppose C₃(x,y) is another quartic that passes through those points, but that is not of the form C₁ + μC₂ for any complex m. It would follow that any quartic of the form C₁ + μC₂ + νC₃ = 0 passes through those points, so we have a two-parameter family of such curves. By choosing suitable values of μ and ν we could find a quartic that passes through the original 13 points plus 2 more arbitrary points, for a total of 15 arbitrary points. This is impossible, so it follows that every quartic passing through the 13 points is of the form C₁ + μC₂ = 0. Consequently every such curve passes through all 16 of the intersection points between C₁ and C₂. This is true for any two distinct basis curves C₁ and C₂ that we might choose, so the extra three points associated with the original 13 arbitrary points are uniquely determined. In other words, for any 13 arbitrarily points on the plane there are three auxiliary points such that any quartic that passes through the original 13 points also passes through the three auxiliary points.

On the other hand, if 14 points are chosen arbitrarily, the 14th will not in general be one of the auxiliary points for the original 13. As a result, a second (distinct) quartic passing through the original 13 points will not in general pass through the 14th point, so the uniqueness of the quartic through 14 arbitrary points is preserved. The fact that two quartics intersect in 16 points does not contradict this, because such a set of 16 points has only 13 degrees of freedom. Once the first 13 points are chosen, the remaining three are fully determined. Almost all sets of 16 points (in fact, almost all sets of 14 points) are not intersection sets for two quartics.

In general, since an algebraic curve of degree d can be fit to d(d+3)/2 points, we gain one degree of freedom by considering the curves of degree d passing through d(d+3)/2 − 1 points, and by Bezout's Theorem we know that two such curves intersect in d² points. Thus, associated with any set of d(d+3)/2 − 1 points in the plane there are

dependent points such that any curve of degree d which passes through the original d(d+3)/2 − 1 points also passes through the (d−1)(d−2)/2 dependent points. This explains why the notion of dependent points does not arise for curves of degree 1 or 2. For curves of degree 3 (i.e., cubics), there is one dependent point for any eight arbitrary points.

It's interesting to consider algebraic curves of degree d = 10. In this case for any given set of 64 arbitrary points there are 36 dependent points such that any tenth-degree curve that pass through the original 64 points also passes through the 36 dependent points, giving a total of 100 points of intersection for two tenth-degree curves. Now, suppose we select two curves of degree 8 with no common factor, and take their 64 points of intersection as basis points for intersections of curves of degree 10. This determines 36 associated points in which those 10th degree curves must also intersect. Now, it might seem that we are faced with another paradox, because the original two octics could be regarded as special curves of degree 10, i.e., curves of degree 10 that just happen to have zero coefficients for all terms of degree higher than 8. This premise leads to a contradiction, because every curve of degree 10 that passes through the 64 basis points also passes through the 36 dependent points, but clearly the two octics do not intersect in those dependent points (because two octics can intersect in no more than 64 points).

This might us to suspect that taking the intersections of two octics as the basis points for curves of degree 10 must lead to dependent points that coincide with the basis points. However, we need not conclude this, because it is not valid to regard the two octics as special curves of degree 10. The proposition that every curve of degree 10 passing through the basis points also passes through the dependent points was based on the fact that every curve of degree 10 can be expressed in the form C₁ + μC₂ = 0 where C₁ and C₂ are any two distinct 10th-degree polynomials passing through the basis points. In general we can select C₁ and C₂ such that they contain non-vanishing terms of degree 9 and 10, not in the same proportion to each other, so that there is no value of μ for which all the terms of degree 9 and 10 in the expression C₁ + μC₂ vanish. Therefore, the two octics need not be of this form, so we are not forced to conclude that the two octics pass through the 36 dependent points.

It would be interesting to explicitly construct an example consisting of two octics intersecting in 8² = 64 points that serve as the basis for the 10² = 100 points of intersection of two 10th-degree curves. I see no reason the 36 dependent points would necessarily be the intersection points of two curves of degree 6, but it's interesting to consider whether this ever occurs. In the words, does there exist a pair of octics that lead to a set of 36 dependent points (for 10th-degree curves) that are the intersection points of two sextic curves? This would be a nice "Pythagorean" partitioning (proportional to 3² + 4² = 5²) of the 100 intersection points for curves of degree 10 into the intersection points of curves of degree 6 and 8. (The connection with the triangular number 10, i.e., the holy tetraktys, would also have appealed to the Pythagoreans.)

Plucker went on to consider the intersections of algebraic curves of unequal degrees. If C_m = 0 and C_n = 0 are curves of degree m and n respectively, with m > n, he considered the family of mth-degree curves expressible in the form C_m + U_m-nC_n = 0 where U_m-n is an arbitrary polynomial of degree m−n. By similar reasoning to that given above, Plucker showed that of the mn points of intersection between C_m and C_n, only mn − (n−1)(n−2)/2 can be chosen independently.

Return to MathPages Main Menu