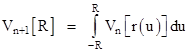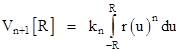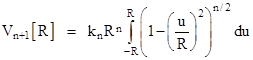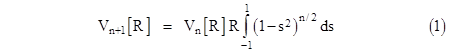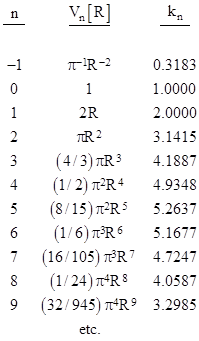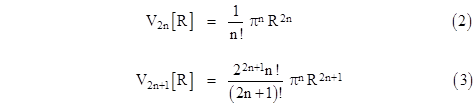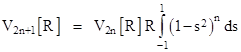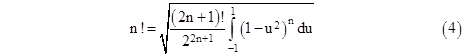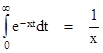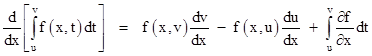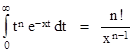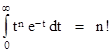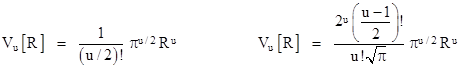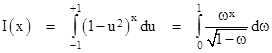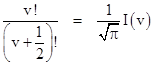Volume of n-Spheres and the Gamma Function

A "sphere" of radius R in n dimensions is defined as the locus of points with a distance less than R from a given point. This implies that a sphere in n = 1 dimension is just a line segment of length 2R, so the volume (or "content") of a 1-sphere is simply 2R. A sphere of radius R in two dimensions can be regarded as consisting of a continuous sequence of one-dimensional spheres at a perpendicular distance u from some fixed 1-sphere, and such that the radius of the 1-sphere at a distance u is r(u) = (R² – u²)^1/2, where u varies uniformly from –R to +R. In general, an n-sphere consists of a sequence of (n–1)-spheres of radius r(u) as u varies uniformly from –R to +R.

Therefore, given the volume formula V_n[R] for n-dimensional spheres, we can determine the formula V_n+1[R] for (n+1)-spheres as follows

Also, it's clear that the volume of an n-sphere must be proportional to Rⁿ, so for every n there is a constant k_n such that the volume of an n-sphere of radius R is given by V_n[R] = k_n Rⁿ.  Thus we have

Inserting the expression for r(u) and factoring out a constant R from the integrand gives

The outside factor on the integrand is simply V_n[R], and if we define the variable s = u/R we have du = R ds, so the above formula can be written as

Using this formula, beginning with the (-1)-dimensional case V_–1[R] = 1/(πR), we can recursively compute the volumes of the higher n-spheres

This shows that the integer dimension with maximum integer coefficient is n = 5. Also, the power of π increases by 1 at each even dimension, and the rational coefficients of the formulas for the sequence of even dimensions (1, 1/2, 1/6, 1/24,...) change by a factor of 1, 1/2, 1/3, 1/4,...etc., whereas the coefficients for the sequence of odd dimensions (2, 4/3, 8/15, 16/105,...) change by factors of 2/3, 2/5, 2/7, 2/9,...etc. Hence we have

By equation (1) we also have

Substituting from the previous expressions for V_2n+1 and V_2n, canceling terms, and solving for n! gives

Notice that if we set n = –1/2 we can evaluate the right hand side, because the factorial in the numerator has the argument 2(-1/2) + 1 = 0. So, evaluating the integral gives the result

This fact, together with the general relation (x+1)! = (x+1)(x!), enables us to easily compute the factorial of any positive half-integer. For example, we have

Furthermore, given all the factorials of the whole and half integers, equation (4) enables us to compute the factorials of all the quarter-integers, because if we set n to a quarter-integer the argument of the factorial on the right hand side will be a half or whole integer. Likewise it follows that we can compute the factorial of any positive 8th-integer, i.e., any number of the form k/8 for positive integer k. From these we can compute the factorials of all numbers of the form k/16, and so on. Thus we have the factorials of all numbers whose binary expansions are finite, and from these we can define the factorial of any positive real number x as the limit of the factorials of finite binary numbers as they approach arbitrarily close to x.

Another approach to defining a continuous function whose value equals the factorial of n for integer arguments n is to consider the sequence of derivatives of 1/x, which gives

In general, the magnitude of the nth derivative of 1/x is n!/x^n–1. Now, we can also express 1/x as the definite integral

Therefore, the successive derivatives of the left hand side equal the derivatives of the right hand side. Recall Leibniz's rule for the derivative of an integral

Since the limits of integration u and v are constants (i.e., independent of x), the first two terms on the right side are zero, so this shows that we can simply bring the partial differentiation inside the integrand. Hence the nth derivative is

Setting x = 1 gives an alternative definition of the factorial function

It's easy to show that this definition satisfies all the same recursive relations as our previous definition (inferred from the formulas for the volumes of n-dimensional spheres), and it has the same "boundary values", so the definitions are equivalent. Notice that both of these definitions are applicable to arbitrary values of n, not just integers. It's customary to express this factorial function in terms of the "gamma function", denoted by the Greek symbol Γ, whose argument is offset by 1 from the factorial, i.e.,

and this function is tabulated in many reference books. Of course, given the values of x! over any unit interval, we can easily compute all other values by means of the relation x! = x(x–1)!

Returning to equations (2) and (3) for the volumes of spheres of even and odd dimensions, we can assert now that those two formulas are equivalent, i.e., if we set 2n in equation (2) and 2n+1 in equation (3) to any positive real value u, we have

Either one of these formulas can be used to give V_u[R]. Equating them gives the relation

Writing u! = u(u–1)! and (u/2)! = (u/2)(u/2 – 1)!, this becomes

Setting u–1 = 2v, this can also be written as

This is called the duplication formula. If we let I(x) denote the definite integral

then equation (4) can be written as

Solving for (2v)! and substituting into (5) gives

Also, equation (6) can be re-arranged to give

which, for integer values of v, furnishes a formula for the “middle” binomial coefficients.

Lastly, we have the relation

Return to MathPages Main Menu