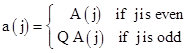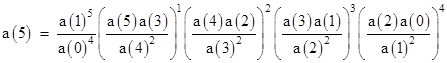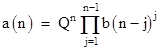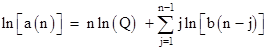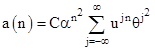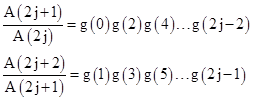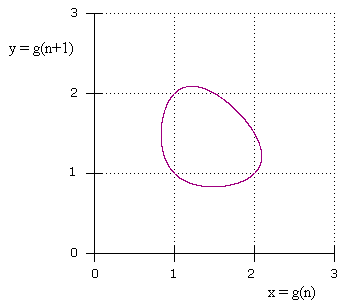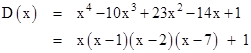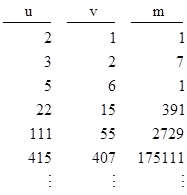|
|
|
Consider the series defined by the recurrence |
|
|
|
|
|
|
|
with the initial values A(0) = 1, A(1) = 1, A(2) = 1, A(3) = 2, and A(4) = 3. The values of this sequence up to A(22) are tabulated below: |
|
|
|
j
A(j)
j A(j) |
|
---
-------------
---- --------------- |
|
0
1
12
22833 |
|
1
1
13
165713 |
|
2
1
14
1249441 |
|
3
2
15 9434290 |
|
4
3
16 68570323 |
|
5
5
17 1013908933 |
|
6
11
18 11548470571 |
|
7
37
19 142844426789 |
|
8
83
20 2279343327171 |
|
9
274
21 57760865728994 |
|
10
1217
22 979023970244321 |
|
11
6161 |
|
|
|
The
recurrence can also be applied in reverse, and since it is formally
symmetrical in both directions, we have A(-j) = A(j). Also, the terms of the sequence
clearly increase at a rate that is roughly proportional to |
|
|
|
|
|
|
|
is a solution of the recurrence (1) for any coefficients C, a, and b, provided q is any root of |
|
|
|
|
|
|
|
This
is just Perrin's polynomial in q4, and the positive real root is q4
= 1.324717957..., so one possible value of q is 1.0728298... To match the
initial values of the sequence we set a = b = 0, so a rough estimate for A(j)
is |
|
|
|
Unfortunately, the non-linearity of the recurrence prevents us from linearly combining solutions, i.e., we can't simply add quadradic powers of the characteristic roots to give a better fit. An alternative approach is to notice that the A terms also satisfies the relation |
|
|
|
|
|
|
|
where p = 2 if j is even and p = 3 if j is odd. This suggests that a more uniform sequence would be given if we could modify the alternate terms of A slightly so that a single recurrence of the form (3) applies to all the terms. Suppose we define the sequence |
|
|
|
|
|
|
|
where Q is some fixed constant. Then we can substitute a or a/Q into equation (3) as appropriate for even j to give |
|
|
|
|
|
|
|
Likewise we can substitute into (3) appropriately for odd j, and then multiply through by Q2, to give |
|
|
|
|
|
The two relations are identical if we choose the constant Q such that 2/Q2 = 3Q2, which implies that Q4 = 2/3. With this Q the initial values of the a sequence are |
|
|
|
|
|
|
|
and the sequence satisfies the recurrence |
|
|
|
|
|
|
|
Again we note that a(-j) = a(j), just as with the A sequence itself. Now in order to arrive at a less rapidly growing sequence, we consider the sequence defined by |
|
|
|
|
|
with the initial values |
|
|
|
|
|
|
|
Dividing equation (4) by a(j)2, we see that it can be expressed in terms of the b( ) sequence elements as follows |
|
|
|
|
|
|
|
Incidentally, although the b sequence satisfies this third-order recurrence with the irrational coefficient, it's not difficult to show that it also satisfies the following fourth-order recurrence with purely rational coefficients |
|
|
|
|
|
|
|
This same recurrence arises when considering the analogous sequences without the Q factors, because each term contains both odd and even indices. We discuss this further at the end of this article. |
|
|
|
The terms of the a sequence can be expressed in terms of the b sequence by means of a "telescoping" identity. For example |
|
|
|
|
|
|
|
Since a(0) = 1 and a(1) = Q, this can be written as |
|
|
|
|
|
|
|
In general we have |
|
|
|
|
|
For numerical purposes it is sometimes preferable to take the natural log of both sides, giving the summation |
|
|
|
|
|
|
|
Letting B denote the asymptotic geometric mean of the terms of the b sequence, we can numerically determine the value B = 1.154022794... Using this value we can define the normalized sequence |
|
|
|
|
|
|
|
This sequence is normalized in the sense that the asymptotic geometric mean of the c terms is 1. We can now expressing the elements of the a sequence as follows: |
|
|
|
|
|
|
|
where |
|
|
|
|
|
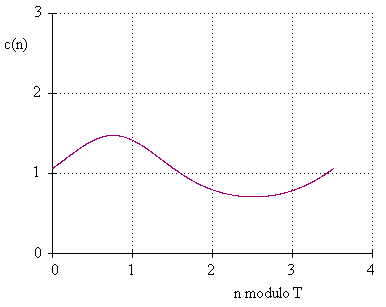
Since the values of Q and B are known, we need only compute the function f(n), which is a product of c terms, to find the value of a(n). Examining the terms of the c sequence, we find that they are cyclical, with a period of roughly 7/2 = 3.5. This is apparent if we plot every 7th point, giving a very low-frequency curve. By plotting every kth point for increasing values of k, we find that an even better "resonance" occurs when we plot every 123rd point, from which we infer that 123/35 = 3.514 is a better rational approximation to the period. Going further, we find that by plotting every 1237th value of q(i) we get an extremely low-frequency signal, so we infer that 1237/352 = 3.514204... is an even better rational approximation of the period. In this way we arrive at an estimate of T = 3.5142040524... for the actual period. A plot of these terms versus the indices modulo T is shown below. |
|
|
|
|
|
|
|
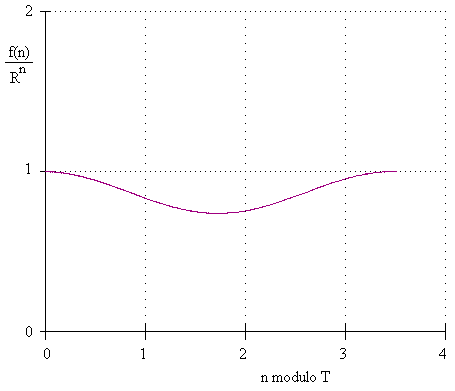
It might seem that the function f(n) should be bounded, since the asymptotic geometric mean of the c sequence terms is unity. However, the c terms do not occur uniformly in any given product f(n), so the asymptotic geometric mean does not necessarily apply. Also, we are not taking the nth root of the cumulative product. As a result, we find that it's necessary to normalize f(n) by a factor of the form Rn, where R is found numerically to equal approximately R = 1.18885806.... A plot of f(n)/Rn versus n (mod T) is shown below. |
|
|
|
|
|
|
|
Remarkably, this conforms almost exactly to a pure (shifted and scaled) cosine function, with the frequency ω = 2π/T = 1.78793... Thus, letting d denote the scale factor, we can represent the function very closely by |
|
|
|
|
|
|
|
Substituting this expression for f(n) into (6), letting σ denote B1/2, and noting that QR = σ, we arrive at |
|
|
|
|
|
|
|
This automatically gives a(0) = 1, and in order to have a(1) = Q we must set |
|
|
|
|
|
|
|
Although (7) is just approximate, it matches the true values very closely. For example, the true value of a(8) is 83, and equation (7) gives 83.00157... The true value of a(20) is (2.27934)1012, and the value given by equation (7) is (2.27928)1012. The deviations can be examined, and higher-order correction terms can be added to (7) to give better and better representations. It's natural to try substituting the expression (7) for a(n) back into the recurrence (4) to see how closely it approaches being an exact solution. This yields the approximate equality |
|
|
|
|
|
|
|
where |
|
|
|
|
|
and
we have set |
|
|
|
|
|
|
|
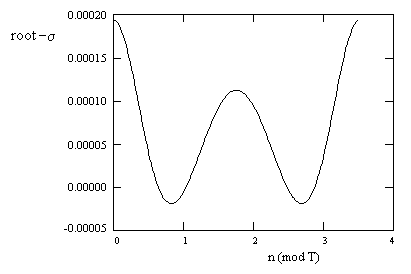
for all indices n. At first this does not look very promising, because the individual coefficients Cj(n) are not constants, nor are they in constant proportion to each other, making it unlikely that any single value of x satisfies this equation for all n. However, remarkably, it is very nearly the case that this equation is satisfied by x = σ for all n. The figure below shows the relevant root as a function of n (mod T). |
|
|
|
|
|
|
|
A more conventional approach to solving recurrence (4) (suggested by Noam Elkies) is to fit the terms to an infinite series of the form |
|
|
|
|
|
|
|
for constants C, α, u, and θ. This can be seen as a generalization of (2). To match the given initial values of a(n) we must have |
|
|
|
C = 0.95768989959... α = 0.788912868537... |
|
u = 0.114194204160... θ = 0.02208942811... |
|
|
|
Combining the summation terms with indices +j and −j, this can also be written as |
|
|
|
|
|
|
|
where r = ln(u). To give a good value of a(20) we must include up to the 7th order term in this sequence. |
|
|
|
In the preceding discussion we focused on the b sequence, which has irrational terms due to the alternating factors of Q. This led to a recurrence (5) with the irrational coefficient P. An alternative approach would be to confine ourselves entirely to rational numbers, and focus on the sequence |
|
|
|
|
|
|
|
with the initial values g(0) = 2 and g(1) = 3/2. This sequence satisfies the recurrence |
|
|
|
|
|
|
|
In terms of this sequence we can express the ratios of consecutive terms of the A sequence as follows |
|
|
|
|
|
|
|
Therefore,
if all the values of g( ) were equal to a single fixed value g, we would have
A(j) asymptotic to |
|
|
|
Now, the values of the g( ) sequence oscillate around a fixed cycle but with an irrational period, so they never actually repeat, but we can determine the orbit of the cycle. To visualize the cycle, note that for any given pair [g(j),g(j+1)] the recurrence (8) enables us to compute the "next" pair, i.e., [g(j+1),g(j+2)], and we can regard these pairs as coordinates [x,y] of points on the plane. The figure below shows the orbit of all such points. |
|
|
|
|
|
|
|
Naturally this locus includes the points (1,1), (1,2), and (2,1), and is symmetrical about the x = y line, because the recurrence is symmetrical forwards and backwards. We can fit the first several points and find that the locus is a simple closed curve given exactly by the equation |
|
|
|
|
|
|
|
which can also be written in the form |
|
|
|
|
|
|
|
This can be studied as an elliptic curve, and the g( ) sequence terms are rational points on this curve. Asymptotically, the iterates are uniformly distributed over this curve, so in principle we could evaluate the geometric mean of the points of this curve. For example, we could integrate the logarithm of x (or y) over this curve. Numerically we find the geometric mean is approximately g = 1.331768502.... , which as expected is equal to B2. |
|
|
|
Solving (9) for y as a function of x gives a quadratic with the discriminant |
|
|
|
|
|
|
|
Therefore, D(g(j)) must be a rational square for all j. In fact, if g(j) = u/v for integers u and v, then there is an integer m such that |
|
|
|
|
|
|
|
Hence the recurrence (8) generates infinitely many solutions of this Diophantine equation. Beginning with g(0) = 2/1 and g(1) = 3/2 we get the solutions |
|
|
|
|
|
|
|
Another sequence is generated by reversing the sign on the right hand side of (1). This gives the recurrence |
|
|
|
|
|
|
|
Taking the initial values 1, 1, 1, 2, 1 gives the integer sequence |
|
|
|
|
|
|
|
Incidentally, the A(n) sequence, formed by the convolution of successive terms, is quite similar to the sequence of coefficients for the power series solution of the equation |
|
|
|
|
|
|
|
as discussed in the note on a Series Solution of a Non-Linear Equation. |
|
|
|
|