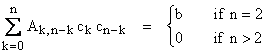|
Series Solution of Non-Linear Equation |
|
|
|
The coefficients of the power series solutions of certain non-linear differential equations are generated by convolutions of the preceding coefficients. One example is the differential equation |
|
|
|
|
|
|
|
Among the solutions of this
equation (with appropriate choices of a,b) are et, sin(t), cos(t),
(A + Bt)n, A + Bt + Ct2, and |
|
|
|
The power series solution of equation (1) can be written |
|
|
|
|
|
|
|
where the coefficients ci satisfy the convolutions |
|
|
|
|
|
|
|
with |
|
|
|
|
|
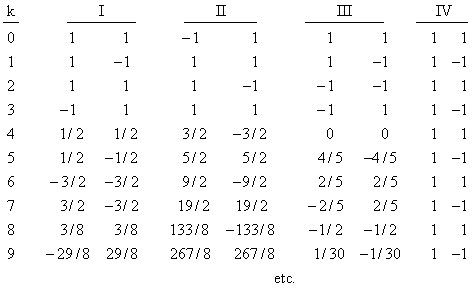
Any choice of c0, c1, c2, and c3, with c1c2 not zero, determines the values of a,b and therefore all the remaining coefficients. There are many interesting things about these sequences of ck values. Focusing on just the sequences with |ck| = 1, k = 0,1,2,3, there are obviously 16 possible choices, but only 8 up to a simple sign change. These 8 can be arranged as four groups of 2: |
|
|
|
|
|
|
|
The coefficients in each group differ only in sign. The coefficients in groups I and II diverge, and those in group IV are all units. Only the group III sequences converge. Interestingly, these coefficients are given very closely by |
|
|
|
|
|
|
|
for k>2, where |
|
|
|
|
|
|
|
Notice that the two possible values of ω sum to 3.1415926... |
|
|
|
The integer numerators and denominators
of these ck sequences also have many interesting properties.
For example, primes p congruent to +1 (mod 4) first appear in the denominator
at cp, whereas primes congruent to −1 first appear at |
|
|
|
|
|
|
|
Incidentally, the value of b in the ubiquitous equation (1) is essentially just a constant of integration, and the underlying relation is the derivative |
|
|
|
|
|
|
|
where q = 3 for unaccelerated separations and q = 2 for (non-rotating) gravitational separations. Isolating q and differentiating again leads to the basic relation, free of arbitrary constants, |
|
|
|
|
|
|
|
Dividing by |
|
|
|
|
|
|
|
|