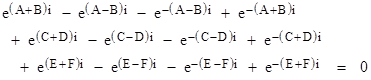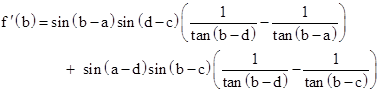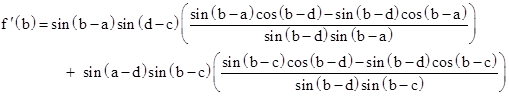On Ptolmey's Theorem

Consider an arbitrary set of six quantities A,B,C,D,E,F that satisfy the relation

What restrictions does this place on the values of A though F?  Recall that the exponential form of the sine function is

so we can write the preceding sum of products in terms of these exponentials, expand the products, and multiply through by −4 to give

To make this sum vanish, the most direct approach is to equate some of the exponents, such as by imposing the equalities shown below

(There are other similar assignments we can make, but it can be shown that they all lead to the same result.)  These conditions enable us to eliminate three of the variables, since they imply

Substituting these expressions for D, E and F into (1) and replacing C with −C, we have the identity

This identity, which applies to any three values A,B,C, is known as Ptolmey's Theorem, and is usually expressed in terms of a quadri-lateral inscribed in a circle as illustrated below:

Recall that the product of the two distances from a point to a circle along any given line is constant (see Quadrilateral in a Circle), so in the left-hand figure we have (AI)(IC) = (BI)(ID), which implies the similarity of opposing triangles.  Also, we know that the angle sub-tended by a given chord from the center of a circle is twice the angle subtended from any point on the circumference (see the note on Loci of Equi-Angular Points), so we can identify the central angles as shown in the left-hand figure.  Obviously the sum of the four basic angles is  a+b+c+d = π.

The length of a chord subtending a central angle of θ is L = 2sin(θ/2), so we have the lengths

Since d = π−(a+b+c) we can replace sin(d) with sin(a+b+c), and we can replace sin(b+d) with sin(a+c).  Now, using the identity (2), we have

which is equivalent to the usual geometric formulation of Ptolmey's Theorem in terms of the edge lengths and diagonals of a quadrilateral inscribed in a circle

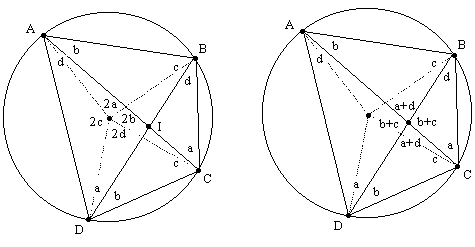
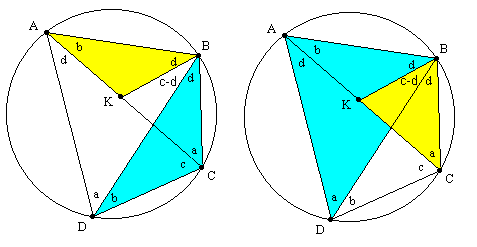
Of course, there's a well-known and very simple geometric proof of Ptolmey's Theorem, which we can describe with the help of the figure below.

If we locate the point K along the line AC such that the angle ABK equals d, then triangle ABK is similar to triangle DBC (as indicated in the left-hand figure above), so we have AB/AK = DB/DC, and hence (AB)(CD) = (BD)(AK).  Likewise the triangle BCK is similar to the triangle BDA, so we get BC/KC = BD/AD and hence (BC)(AD) = (BD)(KC).  Adding these results together gives

This is often specialized to give the addition formulas for the sine and cosine.  For example, if we set C = π/2 in equation (2), and recall that sin(π/2 + x) = cos(x) we have

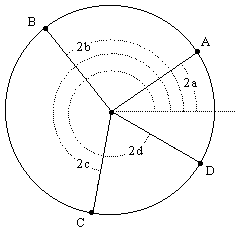
Still, it's interesting that Ptolmey's Theorem can be seen as arising more or less uniquely from the attempt to find solutions of the trigonometric quadratic form (1).  Of course, this can also be inferred directly from the figure, since the length of a chord subtending a central angle theta is 2sin(θ/2) and so if we let 2a,2b,2c,2d denote the absolute angles of the radials from the central point O to the vertices A,B,C,D respectively with respect to the any reference system as shown below

then we have

which can be immediately verified using the exponential form.

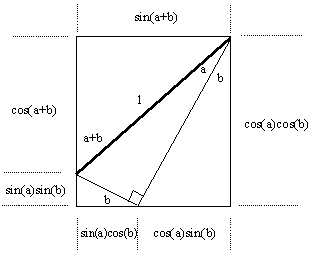
Naturally there are ways of deducing the usual addition formulas for the sine and cosine without relying on Ptolmey's Theorem, since the latter is more general than the former.  The simplest algebraic approach to the addition formulas is just to express the functions in exponential form and multiply them out.  On the other hand, we also have the very simple geometric proof of the addition formulas indicated by the figure below:

From this perspective, the addition formulas are more or less self-evident, and we can use them to give another proof of Ptolmey's Theorem, which is equivalent to the assertion that the function

vanishes identically, where 2a,2b,2c,2d are an arbitrary (ordered) set of central angles.  If we fix a,c,d we can regard this as a function f(b) which we can differentiate with respect to b, giving

Now, we know that f(b) vanishes for at least some sets of angles, such as when the quadrilateral degenerates into a triangle, or when it is a prefect rectangle.  Hence, if we can show that f'(b) vanishes whenever f(b) vanishes, then it will follow that f(b) = 0 for all b, and by symmetry for all a,b,c,d.  To do this, let's first rewrite f ′(b) as follows

On the assumption that f(b) equals zero for some particular b, we can divide through f(b) by tan(b−d) to give

Subtracting this from f ′(b) gives

Rewriting the tangent functions in terms of sines and cosines gives

Canceling sin(b−a) from the first term and sin(b−c) from the second, and using the addition formula for the sine function that we derived independently above, this reduces to

which does indeed equal zero identically.  Of course, f ′(b) = −f(b), so this too vanishes identically (as required).

Return to MathPages Main Menu