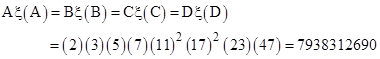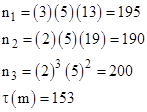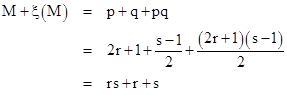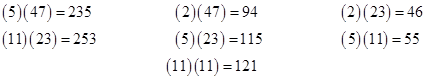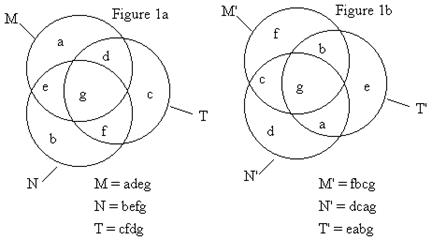
Part 4:  Higher-Order Solutions

Solution Triples:  A set of three distinct integers {M,N,T} such that Mξ(M) = Nξ(N) = Tξ(T) will be called a solution triple. We can partition three such integers into seven co-prime factors a,b,..,g as illustrated in Figure 1a.

Clearly, each of the pairs {M,N}, {M,T}, and {N,T} is a solution pair. Considering the pair {M,N} we note that gcd(M,N) = eg, so the solution kernel of this pair is ad,bf. By Proposition 2 we have

Expanding the left side by the additive property gives

Similarly the solution pair {N,T} leads to the condition

The difference between these last two equations gives a necessary and sufficient condition for {M,N,T} to be a solution triple:

One way of searching for such triples is to generate a list of solution (pair) kernels and then examine these pairs two at a time to determine if they satisfy (4). However, each set of solution pairs actually corresponds to two possible solution triples. Consider the three pairs  {M,N}, {M,T}, and {N,T} illustrated in Figure 1a. The kernels corresponding to these pairs are {ad,bf}, {ae,cf},{be,cd}. Now consider the three pairs {M′,N′}, {M′,T′}, and {N′,T′} illustrated in Figure 1b. The kernels of these pairs are {bf,ad}, {cf,ae}, and {cd,be}, which are identical to the pairwise kernels for {M,N,T}, in spite of the fact that {M,N,T} and {M′,N′,T′} are distinct. This occurs because there is a permutation of the components a,b,..,f  that leaves the pairwise kernels unchanged (except that the components are transposed). Specifically, the permutation consisting of the three transpositions

produces a new triple with the same pairwise kernels. We refer to these two triples as duals of each other.

Given two solution kernels {u,v} and {r,s}, we could make the assignments

and then compute the individual components as follows

If these components satisfy (4) then we call the integers a,b,..,f a triple kernel. We can then use (3) to compute ξ(g). For any g having this value of ξ(g) the integers M = adeg, N = bfeg, T = cdfg constitute a solution triple.

On the other hand, given the same solution pairs {u,v} and {r,s}, we could equally well make the assignments

in which case the individual components are given by

If these components satisfy (4) then the integers M′,N′,T′ as defined in Figure 1b are a solution triple. As an example, consider the two solution pairs {12,11} and {22,19}. If we make the assignments

then we have the components

which gives the three integers (according to Figure 1a)

These numbers do not constitute a solution triple, since the components fail to satisfy equation (4). However, the "dual" of this triple gives the components

yielding the three integers

which do satisfy the requirements of a solution triple with g defined such that ξ(g) = 18.

Evidently any number of triple kernels can be found in this way. Table 4 contains several that can be produced from the double kernels of Table 1, but evaluating only one of the two possible permutations in each case, so the list is incomplete. The smallest solution triple is

which is based on the kernel

taking g = 21.

We observe that most of the kernels listed in Table 4 have at most only one of a,b,c > 1. Also, it appears that the six integers

constitute a triple kernel if and only if  u,v  and  u,w (allowing transpositions) are double kernels with q(u,v) = q(u,w).

Higher Order Solution Sets:  Similarly we can determine sets of 4 integers A,B,C,D such that

Aξ(A) = Bξ(B) = Cξ(C) = Dξ(D)

and Table 4 provides several examples. One such 4-solution consists of the integers

which satisfy the equality

The extended Table 4 also gives examples of 5-solutions. If we define

then the integers

for any k such that ξ(k) = 52 constitute a 5-solution. This is equivalent to the statement that the set of primes

S = {2,2,3,5,11,17,19,29,59,71,89}

contains 5 distinct subsets s₁, s₂, ..., s₅ such that

where

If we add the prime 47 and another 5 to S, then the 52 in the above equation vanishes. However, the primes 5 and 47 are, in a sense, inert elements of the set. (We consider later whether there are such sets with no inert elements.)

We might remove the restriction that the elements of S be primes, and instead search for sets of general integers such that

A further generalization is to allow the constant to be negative. The subsets s_i may or may not be disjoint and covering (as they are in the preceding example).

Finding Solution Sets of Order k:  Proposition 4 stated that  {m,n} constitutes a solution kernel if and only if the quantity

is a positive integer. This can be rewritten in the form

which is true if and only if

(because we can expand the ξ functions and subtract ξ(q) from both sides). It follows that for any two integers M and N such that M + ξ(M) = N + ξ(N)  and  gcd(M,N) = q,  where q is any positive integer, the integers M/q and N/q constitute a solution kernel.

This can be immediately generalized to solution sets of k elements. For any positive integer c let χ(c) denote the number of integers n such that  n + ξ(n) = c. (This is called the valence of the function G.)  Also, let τ(c) denote c minus the sum of the values ξ(n) over this set of  n values. Then, given this set of k integers n₁, n₂, ..., n_k such that

we can construct a set of integers N₁, N₂, ..,N_k such that

by taking

where the quantities u_j and s are defined by

and ξ^-1 signifies the inverse ξ function. Thus, the right-hand factor in the expression for N_j is an integer b such ξ(b) = τ(c) + ξ(s). (In general the function ξ^-1 is multi-valued.)  This requires that τ(c) + ξ(s) be positive.

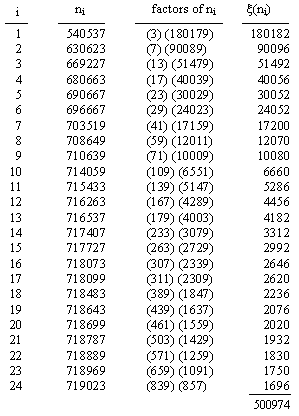
Thus, every integer c with χ(c) = k and  τ(c) + ξ(s) > 0  corresponds to a solution set of k elements. It is conjectured that the converse is also true, i.e., that every solution set of k elements is associated with an integer c for which χ(c) is equal to (or greater than) k. The values of χ(c) and τ(c) and the n_i for each integer c from 1 to 100 are listed in Table 5.

It's useful to consider an example. The first "triple" in Table 4 is defined by the values

This gives the family of solution triples

where g = ξ^-1(165). This same triple is represented in the extended Table 5 where, for c = 216, we find

which gives

and

s   =   gcd(38000, 39000, 37050)   =   50

Noting that ξ(s) = 12, we see that this gives the same family of solution triples as found in the earlier table.

Discussion:  We could simply have factored  s  out of the three integers (n₁n₂), (n₁n₃), (n₂n₃)  and asserted the solution triples  {760q, 780q, 741q}  where now  q = 50 ξ^-1(153). These values of q are a subset of the values of  g = ξ^-1(165). However, they do not constitute the complete set, because there are integers g for which ξ(g) = 165 but which are not divisible by 50. For example, g = (163)(2). This arises because of the non-uniqueness of the inverse ξ function.

Very High Order Solution Sets:  Table 6 gives the first few values of c for which χ(c) equals 1, 2, ..., 24. Presumably, for any given positive integer k there are infinitely many c such that χ(c) = k. The smallest integer c such that χ(c) = 12 is 14399. This leads to the 12-kernal with the values of n_i shown below:

In this case c = 14399, the sum of the ξ(n_i) is 13400, and the n_i have no common factor, so b is any integer such that ξ(b) = 999.

The next smallest integer c for which χ(c) = 12 is 15119. The corresponding values of n_i are as follows

In this case the sum of the ξ(n_i) is greater than c, and the n_i have no common factor, so we have ξ(b) = –2759, which is not satisfied for any integer b.

To give another example of a very high order solution set, we note that χ(720719) = 24, which implies the existence of the 24-kernel presented in the following table.

This table shows that τ(720729) = 219745 and there are no common factors in the n_i. Therefore, we can construct a family of 24-solutions using the formulas given above. The number of solutions in this family is equal to the number of prime partitions of 219745.

Each value of n_i in this 24-solution is of the form p_iq_i where p_i and q_i are primes such that

An efficient way of searching for such solutions is to observe that we can add 1 to both sides and factor the resulting equation as follows:

Therefore, we need only determine the two-part multiplicative partitions ab = c + 1 such that a-1 and b-1 are primes. In the present case we have c = 720719, so we need to examine the factors of

c + 1  =  720720  =  (2)⁴(3)²(5)(7)(11)(13)

Cunningham Chains:  The is an obvious tendancy for the n_i factors to be primes of the form p = 2q+1 where q is also a prime. Sequences of primes with this property are called Cunningham chains. The first two Cunningham chains of unusual length are

If N = rs for primes r and s then N + ξ(N) = rs + r + s. Now, if M = pq where p = 2r + 1 and q = (s-1)/2 (both primes), then we have

Thus, by forming a sequence of integers given by multiplying the elements of a Cunningham chain in increasing order times the elements of a chain in decreasing order gives integers with the same value of N + ξ(N). For example, the smallest set of 11 integers with equal G functions is

In this case c = 4319 so ξ(b) = -159, which means that this set cannot be used to construct an 11-kernel. However, this clearly illustrates how Cunningham chains can be used to produce solution sets. We can also explain several of the 3-kernels by considering the convoluted chains

It is conjectured, but not proven, that there exist Cunningham chains of any finite length, which would imply the existence of solution sets of arbitrary size.

Return to Table of Contents