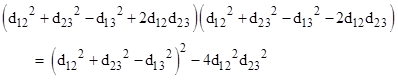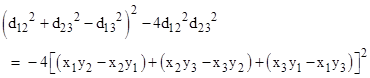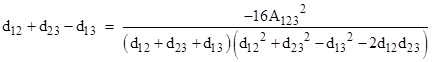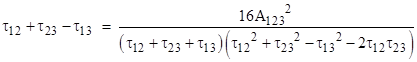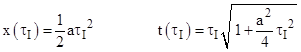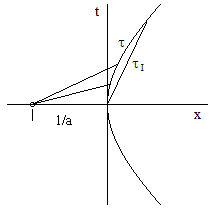Curved Paths and Linear Segments

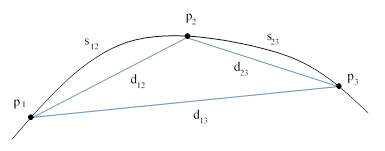
Let p₁, p₂, p₃ denote three points on an arbitrary curve in a plane surface, and let s_ij denote the path length along the curve from p_i to p_j as depicted in the figure below.

The symbols d_ij denote the distances between the points p_i and p_j. Clearly we have s₁₃ = s₁₂ + s₂₃, but d₁₃ is not generally equal to d₁₂ + d₂₃. To quantify the extent to which the linear distances are not additive, we can construct Cartesian coordinates x,y and then we have

We seek the quantity d₁₂ + d₂₃ – d₁₃, and we can multiply this by the “conjugate” factor to give

We can then multiply this by another “conjugate” factor as follows

The expression factors to give

The quantity in square brackets is just 2A₁₂₃ where A₁₂₃ is the signed area of the triangle with vertices p₁, p₂, p₃. Therefore, we’ve shown that

This vanishes just if the area of the triangle is zero, which occurs just if the three points are co-linear. If we require this quantity to vanish for every set of three points on the curve, then the curve must be a straight line.

The same approach applies to spacetime intervals as well, for which the elapsed proper time along any uniform (unaccelerated) timelike path between two events e_i and e_j is given by the pseudo-metric line element

Proceeding exactly as above, we find that only the sign is different in the result

where A₁₂₃ is the signed “area” given by

As an aside, we note that, beginning from rest at the origin of a standard inertial coordinate system x,t and undergoing constant proper acceleration a in the positive x direction, the coordinate time and spatial position of a particle at the elapsed proper time of τ are given by

The trigonometric identity 1 = cosh² – sinh² implies that

Letting τ_I denote the magnitude of the inertial interval from the origin to x,t, this relation gives

This is shown in the figure below.

The expression for x(τ_I) happens to take the same form as Galileo’s original expression for constant acceleration, although the physical meaning is quite different, because τ_I is neither the coordinate time t nor the proper time τ along the particle’s trajectory.

Return to MathPages Main Menu