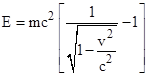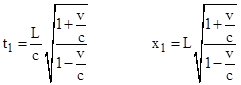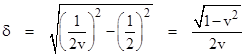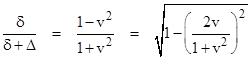Muons, Clocks, and Intervals

Everything is obvious, once you know the answer.

                                               Duncan Watts

The Muon Befuddlement

One of the most common confusions involving special relativity is the claim that the relativistic effects involving the decay of muons entail a contradiction. As with nearly all elementary misunderstandings involving special relativity, this is due to failure to account for the relativity of simultaneity.

Recall that a commonly cited example of observable relativistic effects is the fact that although the half-life of a muon is only about 2.2 μsec, a high-speed muon created in the upper atmosphere (as part of the secondary shower of particles created by incoming cosmic rays colliding with the atoms in the atmosphere), generally persists for a considerably longer time in terms of the inertial coordinates in which the earth is at rest. This is due to relativistic time dilation, i.e., the elapsed proper time of the muon moving at speed v in the earth’s frame runs slow by the factor √(1−v²), so the half-life is increased by the reciprocal of that factor. (Throughout this discussion we use units such that c=1.)

So, if a muon is created in the upper atmosphere at an altitude of h above the ground, and moves vertically downward at speed v in terms of the ground inertial coordinate system S to a collision with the ground, the elapsed time in terms of S between the creation of the muon and the collision is h/v, whereas in terms of the system S′ of inertial coordinates in which the muon is at rest the elapsed time between creation and collision is just (h/v)√(1−v²).

Now, the student may think this entails a contradiction, because he says that, according to the principle of relativity, in terms of S′ a clock on the ground runs slow by the factor √(1−v²), and therefore (he reasons) the elapsed time for a clock on the ground (at rest in S) between the creation of the muon and its collision with the ground should be (h/v)(1−v²), contradicting the already-stated fact that it is really h/v. 

The analogous claim can also be expressed in terms of the distances due to length contraction. The student thinks that relativity implies the distance between the muon at its creation and the surface of the earth has contradictory values.

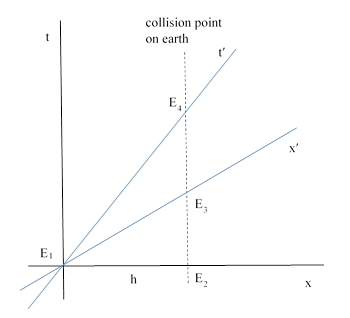
The confusion is dispelled simply by pointing out the relativity of simultaneity.  Let us consider the inertial coordinate systems S and S′ with common origin at the creation of the muon, as shown in the figure below. The positive x direction is in the downward direction along the muon’s path.

The muon is created at event E₁, which is simultaneous with event E₂ on the ground in terms of S, and simultaneous with event E₃ on the ground in terms of S′. The collision occurs at event E₄. By stipulation the coordinates (x,t) in terms of S of the four noted events are (0,0), (h,0), (h,vh), and (h,h/v) respectively. Thus for a clock sitting at the collision point the elapsed proper time between the creation of the muon and the collision in terms of S is the interval from E₂ to E₄, which has magnitude h/v, and the elapsed proper time between the creation of the muon and the collision in terms of S′ is the interval from E₁ to E₄, which has magnitude (h/v)√(1−v²).

The student may then ask about the elapsed time on a ground clock between “when” the muon is created (in terms of the muon’s rest system S′) and when it collides with the ground. This is the elapsed time from E₃ to E₄, which is (h/v)(1−v²). For example, if v = (1/2)√3 and h/v = 4.4 μsec, then the elapsed muon time between creation and collision is 2.2 μsec, the elapsed ground time using the simultaneity of the ground system is 4.4 μsec, and the elapsed ground time using the simultaneity of the muon system is 1.1 μsec. These represent the magnitudes of the intervals from E₁ to E₄, from E₂ to E₄, and from E₃ to E₄, respectively. Hence the magnitude of the interval from E₂ to E₃ is hv.

Likewise the spatial distance between the muon at creation and the point of collision on the ground is the magnitude of the interval E₁ to E₂ in terms of S, and the magnitude of the interval E₁ to E₃ in terms of S′. These have the values h and h√(1−v²) respectively. Clearly there is nothing contradictory or paradoxical about these simple facts, once we correctly account for the relativity of simultaneity. As an aside, we note that the product of the magnitudes of the six intervals between these four events is h⁶(v – 1/v)².

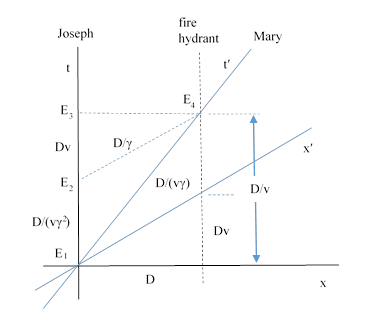
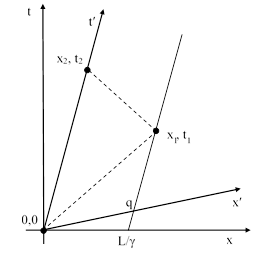
For a closely related (in fact, essentially identical) example, suppose Joseph is stationary on the road, and suppose Mary zooms past him at speed v in terms of Joseph’s co-moving inertial coordinate system S. As she passes adjacent, a spark jumps between them. We call this event E₁. Mary then continues on her path, and passes a fire hydrant at a distance D from Joseph, and another spark occurs as she passes adjacent. We call this second spark event E₄. Thus, in terms of S, the time between sparks is D/v, and Mary’s elapsed proper time between the spark events from E₁ to E₄ is D/(vγ) where γ = 1/√(1−v²). This is depicted in the figure below.

Mary is present at both sparks, but Joseph is present at only the first spark, so if we want to determine Joseph’s elapsed proper time “between the sparks” we need to map the second spark onto Joseph’s world line. Event E₂ is the event at which Joseph is simultaneous with the second spark in terms of Mary’s co-moving inertia-based coordinates, whereas E₃ is the event at which Joseph is simultaneous with the second spark in terms of his own co-moving system of inertia-based coordinates. We see that, in terms of Mary’s co-moving inertial coordinates, Joseph between the times of the two sparks moves a spatial distance –D/γ in the time D/(vγ), so his elapsed proper time during that interval from E₁ to E₂ is D/(vγ²). On the other hand, in terms of Joseph’s co-moving inertia-based coordinates he has not moved spatially between the times of the sparks, and his proper time has advanced by D/v from E₁ to E₃.

Observations of the muon flux for atmospheric muons at different elevations are often cited as evidence in support of special relativity, and of course they are perfectly consistent with special relativity – provided we know the velocity v of the subject muons in terms of the inertial rest coordinate system of the ground. But how do we determine this speed? In practice, the experimenters focus on muons of a certain energy, which can be measured as the muon impinges on the apparatus, and according to special relativity this kinetic energy E is related to the velocity v by

But we obviously can’t simply invoke special relativity to assert this relationship in order to test special relativity, as that would be circular reasoning. The interpretation of the results of muon observations rests on the experimental demonstrations of this relationship, e.g., prior measurements of the velocity and energy of particles in accelerators, in which the velocities of the particles are evaluated empirically in terms of the inertia-based coordinates of the apparatus. This is true in general – all experimental demonstrations of special relativity, if examined closely, can be traced back to reliance on the empirical relationship between energy and inertia. That relationship is both necessary and sufficient to empirically establish local Lorentz invariance.

The Longitudinal Light Clock

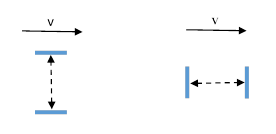
Another common confusion concerning elementary special relativity involves the so-called “light clock”. This is a conceptual construction sometimes used to illustrate relativistic time dilation, although some students think it represents a derivation of time dilation, which is not true when presented in just the transverse form, as depicted in the left-hand figure below.

Letting L denote the spatial “rest distance” between the mirrors (i.e., the spatial distance in terms of inertia-based coordinates in which the mirrors are at rest), so the time for a pulse to complete a round trip is 2L/c. A bouncing pulse of light in the transverse orientation would move a distance vΔt for one transit, where Δt is the time (in terms of S) for the transit. Hence the squared spatial distance is s² = L² + v²Δt², and we also have s = cΔt, so we can substitute for s and solve for Δt and double to give the round trip time 2Δt = (2L/c)γ where γ = 1/√(1 − v²/c²).

But this, by itself, doesn’t represent a derivation of time dilation, let alone of the Lorentz transformation, because it has not considered the longitudinal case shown in the right-hand figure above. As discussed in Corresponding States, this unavoidably entails length contraction, but the typical presentation doesn’t make the necessary inferences, and simply applies the Lorentz transformation, so they don’t present the actual derivation, just a demonstration of consistency. Still, even this demonstration is sometimes confusing to students. The path of a pulse is as shown below.

The magnitude of the spacelike interval from the origin to the event q is L, and the leading mirror crosses the x axis at L/γ. We have x₁ = L/γ + vt₁, and also x₁ = ct₁, from which we get

We also have x₂ = vt₂ and (x₂ − x₁) = −c(t₂ − t₁), which implies (c+v)t₂ = 2ct₁, and hence solving for t₂ and substituting from the above for t₁ we get t₂ = (2L/c)γ, just as for the transverse orientation. Needless to say, we’ve made use of length contraction without giving the explanations (as in Corresponding States) for why the length contraction is logically implied, so the discussion here is just a verification of consistency.

Two Rows of Clocks

The reciprocity of the Lorentz transformation is exemplified by the fact that, given two relatively moving clocks, each clock runs slow in terms of the inertial-based coordinates in which the other is at rest. This sometimes confuses people, thinking that it implies real numbers x and y representing the rates of the clocks such that x < y and y < x. This of course is not correct. Letting x,t and x′,t′ denote inertia-based coordinates moving with relative speed v in terms of which the two clocks are at rest, and letting τ and τ′ denote parameters representing the proper times of the two clocks, we have the relations dτ/dt′ < dτ′/dt′ and dτ′/dt < dτ/dt. Thus there is nothing contradictory or paradoxical about this. To be explicit, we have dτ/dt = dτ′/dt′ = 1 and dτ/dt′ = dτ′/dt = √(1−v²).

Those expressions involve total derivatives along the worldlines of the clocks, but we can also express the relevant relations involving the time coordinates of the two systems purely in terms of partial derivatives of the coordinates, i.e., (∂t′/∂t)_{const x}  =  (∂t/∂t′)_{const x′} = 1/√(1−v²).

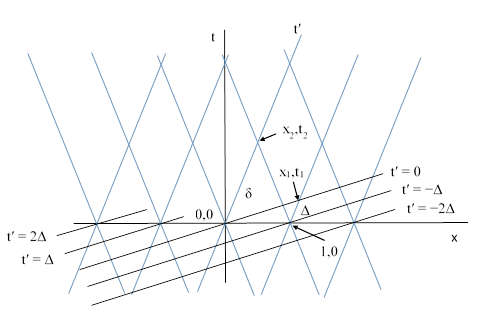
To illustrate these reciprocal relations in concrete terms, consider two parallel rows of identically-constructed clocks moving along the x axis of an inertia-based coordinates system S with the speeds v and –v respectively, and suppose they cross the x axis at unit intervals, as shown below.

We can infer the coordinates x₁,t₁ from the intersection of t₁ = vx₁ and x₁ – 1 = vt₁, from which we get x₁ = 1/(1 – v²) and t₁ = v/(1 – v²). With this we can compute the time skew per unit distance

We also have x₂ = 1/2, t₂ = 1/(2v), from which we get the proper time for each clock between encounters

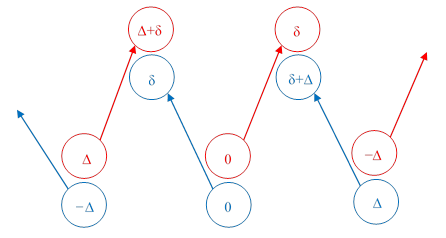
The readings of the rightward moving clocks at time t = 0 are …2Δ, Δ, 0, −Δ, −2Δ, … and by symmetry the readings of the corresponding leftward moving clocks at t = 0 are …−2Δ, −Δ, 0, Δ, 2Δ, … respectively. Each clock undergoes an elapsed time of δ between encounters, so when the central rightward clock (which reads 0 at t = 0, adjacent to a rightward clock that is also reading 0) meets the next leftward clock (which reads Δ at t = 0), they have both advanced by δ, so the ratio of the elapsed time for the rightward clock  to the difference between the readings of the leftward clocks is

Clearly the same applies to every other clock and consecutive encounters, i.e., the elapsed time between encounters is √(1−u²) times the difference in the readings of the encountered clocks, where u = 2v/(1+v²) is the relative velocity between the rows. This is depicted in the figure below.

For purposes of giving a simple illustration of these relations, we can choose v = 1/√3 which gives δ = Δ, and then we can just denote the clock readings by rows of integers. At t = 0 we have the two rows

In the next set of encounters all the times are incremented by 1, and the upper row is shifted left and the lower row is shifted right, so we have

The left-most clock on the lower row read 8 when it was adjacent with the clock reading 1 on the upper row, and then it read 9 when it was adjacent to an upper clock reading 3, so it advanced only half as fast at the adjacent readings on the upper clocks.  Likewise the right-most clock on the upper row read 8 when it was adjacent to the clock on the lower row reading 1, and then it read 9 when it was adjacent to the lower clock reading 3. The same applies to every clock in both rows, i.e., each clock is advancing only half as fast as the readings on the clocks in the adjacent row as it passes them.

A Decent Interval

The word “interval” is sometimes used in discussions of special relativity, but some of the people who use this word seem to be suffering from an odd cognitive dissonance. This is well-illustrated in Feynman’s physics lectures, where he says

The square of the spatial distance [from the origin] is x² + y² + z². Now what about spacetime? It is not hard to demonstrate that we have here, also, something which stays the same, namely, the combination c²t² – x² – y² – z² is the same before and after the transformation…This quantity is therefore something which, like the distance, is “real” in some sense; it is called the interval between the two spacetime points… (Actually, of course, it is the interval squared, just as x² + y² + z² is the distance squared.)

We’re grateful for the parenthetical clarification, but if it’s so obvious that the noted quantity is the squared interval, why does he first define the interval as the squared value, only to immediately reverse himself? The two quantities don’t even have the same units. Since “interval” is said to be analogous to distance, the quadratic quantity must clearly be the squared interval, just as the sum of squares of the components is the squared distance. He might just as well have begun by saying that x² + y² + z² is the distance, and then saying parenthetically that, of course, it not actually the distance, it is the squared distance.

Rindler’s Essential Relativity unambiguously defines Δs² as the squared interval, as does D’Inverno’s text. Likewise Penrose refers to the integral of √(g_mndx^mdxⁿ) as the interval along the curve (note the square root).

However, other references, such as the McGrath-Hill Dictionary of Physics and Mathematics, define Δs² as the interval, and never bother to correct themselves (as Feynman did). Many online references also exhibit the weird definition. For example, the Wikipedia article on spacetime says the spatial distance Δd is defined by (Δd)² = (Δx)² + (Δy)² + (Δz)², and then says in relativity the spacetime interval is the analog of the distance, but it then states that the spacetime interval is (Δs)², rather than Δs. Hence it is saying (Δs)² is analogous to Δd, which clearly makes no sense.

These low-quality references may have taken their cue from one or two particular texts, such as Bernard Schutz’s popular book “Gravity from the Ground Up”, in which he explicitly makes the bizarre definition and even tries to justify it (albeit senselessly):

The spacetime-interval between the two events is the quantity s² = x² − c²t². Notice that this is written as the square of a number s. The spacetime-interval is the quantity s², not s. In fact, we will not often deal with s itself. The reason is that s² is not always positive, unlike distance in space. If ct is larger than x then s² will be negative. In order to avoid taking the square-root of a negative number, physicists usually just calculate s² and leave it at that. You should just regard s² as a single symbol, rather than as the square of something.

This is absurd, since spacelike and timelike intervals Δs and Δτ are the actual positive measured quantities, given by √(Δx² – Δt²) and √(Δt² – Δx²) respectively. (Of course nothing prevents us from selecting the negative roots.) To say that we “rarely use” proper distances and proper times is ridiculous. This is the sort of confused reasoning that seems prevalent among people who were taught that “relativity is geometry”, and who then struggle with the fact that the Minkowski line element is not actually a metric at all, it is a pseudo-metric, since (for example) it doesn’t even satisfy the triangle inequality. In extreme cases (as the quote above) this leads to denial of the actual measured quantities. Apparently there is a popular text by Wald that presents the same weird definition, which is then parroted by other authors.

Another shortcoming of some common usages is that using the word “interval” to refer to the scalar pseudo-metrical “distance” between two events leaves us with no word to refer to the straight locus of events in spacetime between two given events. One solution would be to use the word “interval” to refer to this locus (similar to a displacement vector), and to distinguish between spacelike and timelike intervals. Then for an interval with components Δx and Δt in terms of any given system of inertia-based coordinates we define the magnitude of the interval as √(Δx² – Δt²) if it is spacelike and √(Δt² – Δx²) if it is timelike.  (We using units with c=1.)

Of course, the concept of extended spacetime intervals as functions of two events applies only in flat spacetime, since in curved manifolds there is not generally a unique geodesic locus between two given events. Thus the integrated distance from the origin is not a state variable, because it is path dependent. Nevertheless, as Penrose notes, we can always define the interval along a curve, and this is given not by integrating (dτ)² but by integrating dτ. Clearly the only sensible nomenclature is to refer to the incremental interval along a (timelike) path as dτ, not (dτ)². If there is some coherent conceptual advantage to assigning the word “interval” to the negative of the square of dτ, it has not been articulated in the literature.

Return to MathPages Main Menu