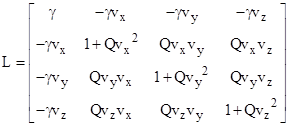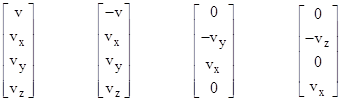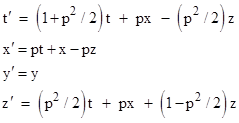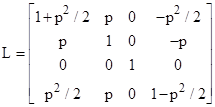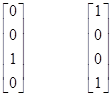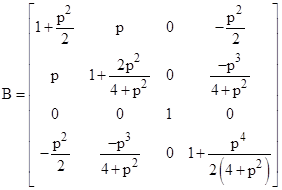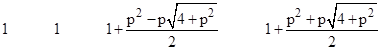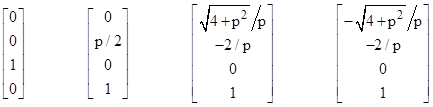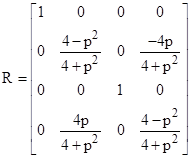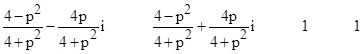Eigenvectors of Lorentz Transformations

Your bait of falsehood takes this carp of truth:

And thus do we of wisdom and of reach,

With windlasses and with assays of bias,

By indirections find directions out:

So by my former lecture and advice,

Shall you my son. You have me, have you not?

                                          Shakespeare

To determine the Lorentz transformation for a pure boost with the velocity vector v_x,v_y,v_z in terms of a given system S of inertia-based coordinates, we can spatially rotate (re-orient) S such that the velocity v = (v_x² + v_y² + v_z²)^1/2 is purely in the x direction, then apply a simple boost in the x direction, and then spatially rotate back. This leads uniquely to the pure boost

where γ = (1−v²)^1/2 and Q = (γ–1)/v². The eigenvalues of this transformation are

(the first two of which are just the approaching and receding Doppler factors), and the corresponding eigenvectors are

The first two are light-like vectors (noting that the magnitudes of the spatial and temporal parts are both v), whereas the remaining two are purely spatial in these coordinates, perpendicular to the velocity vector, one in the xy plane and the other in the xz plane. The repeated eigenvalue also corresponds to the eigenvector

which is perpendicular to the velocity vector in the yz plane. In general the direction of any purely spatial vector that is perpendicular to the velocity vector is unchanged by the transformation. Likewise the directions of the light-like vectors in the spatial direction of the boost are also unchanged by the transformation.

For another example, recall that any proper orthochronous Lorentz transformation (including ordinary rotations and relativistic boosts) can be represented by X′ = MXM* where

and M* is the transposed conjugate of M. The coefficients a,b,c,d of M are allowed to be complex numbers, normalized so that ad – bc = 1. This is discussed in in the note on Null Coordinates. Two observers at the same event in spacetime but with different orientations and velocities will "see" incoming light rays arriving from different relative directions with respect to their own frames of reference, due partly to ordinary rotation, and partly to relativistic aberration.  It can be shown that the effect of a Lorentz transformation on the incidence angles of light rays at an event corresponds precisely to the effect of a particular linear fractional transformation on the Riemann sphere via ordinary stereographic projection from the extended complex plane.

If we apply a Lorentz transformation specified by the four complex coefficients a,b,c,d, the resulting change in the directions of the incoming rays of light is given exactly by applying the linear fractional transformation

to the points of the extended complex plane. For a simple example, consider the linear fractional transformation w → w + p for some constant p, which corresponds to the Lorentz transformation

Thus the Lorentz transformation matrix is

This is not a pure boost, it is composed of a rotation and a boost. The eigenvalues of this transformation are 1, 1, 1, 1, and the representative eigenvectors are

The right hand eigenvector is a light-like vector in the spatial z direction. The other is a spacelike vector in the y direction. Although the transformation corresponds to a very simple linear fractional transformation w + p for the ray direction (under stereographic projection), it is not symmetrical in the x, y, z directions of space.

We can express L as a product of a pure boost B and a pure spatial rotation R as L = RB. The boost is given by

The eigenvalues of this transformation are

and the corresponding eigenvectors are

As required, the second two are light-like, and the first two are spatial and perpendicular to the spatial directions of the light rays. The rotation transformation R is given by

The eigenvalues of this transformation are

and the corresponding eigenvectors are

The third of these is pointing in the time direction, because this is a purely spatial rotation that doesn’t affect the time coordinate. The fourth is in the y direction, because the rotation is about the y axis, which is left unchanged. The first two eigenvectors, corresponding to the complex eigenvalues, are in complex directions.

Return to MathPages Main Menu