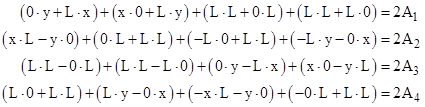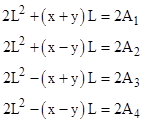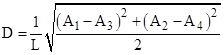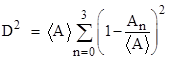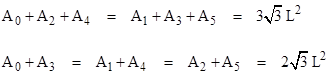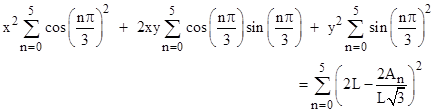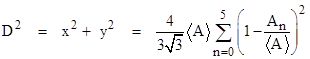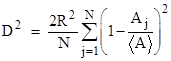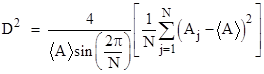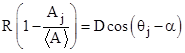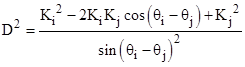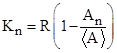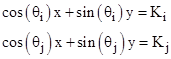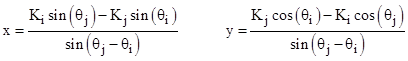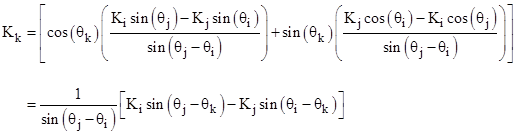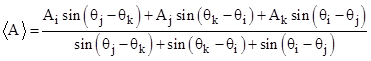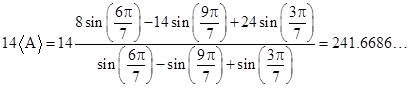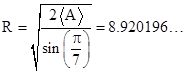Partitioning Polygons

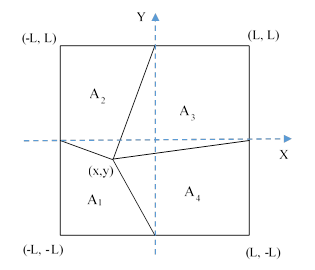
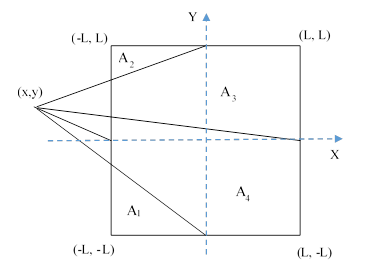
Suppose we have a square with edge length 2L, and from the midpoints of each edge we draw lines to some single point as illustrated below.

In this figure, x and y are the coordinates of the point where the lines meet. We can see immediately that the pairs of opposite regions have equal areas, i.e., A₁ + A₃ = A₂ + A₄. To show this, draw lines from the vertices of the square to the intersection point, and note that by altitude and base argument each triangular region of one pair has area equal to that of an adjacent triangular region of the other pair.

To relate the areas of the four regions to the coordinates of the intersection point (in terms of a Cartesian coordinate system with origin at the square’s center), we can use the standard formula for the signed area of a polygon in terms of the coordinates of the vertices, giving the four equations:

Simplifying these expressions, we get

The sum of the first and third equations equals the sum of the second and fourth, so we have

which confirms that each pair of opposite regions has half the area of the square. Solving this for L and substituting into the first and fourth equations gives

Thus we can solve these equations to give the coordinates of the meeting point

Conversely, given the value of L and the coordinates of the point (x,y), we can compute the four signed areas by the expressions given previously.

The distance D from the center of the square to the intersection point is

Re-numbering the indices from 0 to 3 and defining <A> = L² as one fourth of the total square, another expression for this distance (derived by the same method used for the hexagonal case below) is

Note that the intersection point need not be in the interior of the square. The figure below shows a case with an external point.

Two of the resulting quadrilaterals have crossing edges (in a figure 8 pattern), so the areas are the counter-clockwise signed values.

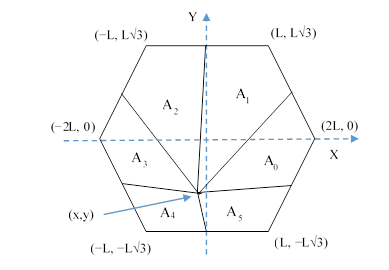
Now consider the analogous figure for a hexagon, partitioned by lines from the midpoints of the edges to some specified intersection point as illustrated below.

By the same method as with the square, we can write the six signed areas as

for n = 0, 1,…, 5, where θ is an arbitrary orientation angle of the hexagon relative to the coordinate system, equal to the angle between the positive x axis and the line from the origin to the outer vertex of the A₀ region. In the figure above we have θ = 0, and so the explicit expressions for the areas are

Thus we have the two identities

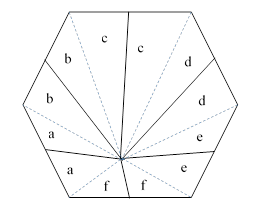
These relations can be understood in terms of the figure below, where lower-case letter signify the areas of the respective triangular regions.

The equality of the areas of the two regions marked “a” (for example) follows from the two triangles being on equal bases with equal altitudes. The first identity follows immediately from the fact that A₀+A₂+A₄ and A₁+A₃+A₅ both equal the sum a+b+c+d+e+f.

On the other hand, the identity A₀ + A₃ = A₁ + A₄ signifies that e+d+b+a = d+c+a+f, which is true just if b+e = c+f. The latter equality is true, as can be seen from the fact that the bases and sum of altitudes of f and c are the same as for b and e. In fact, every pair of opposite slices have the same combined area. Thus we have a+d = b+e = c+f.

Given one of the pairs of areas with indices 0,3, or 1,4, or 2,5, we can compute L. Also, given either of the triples 0,2,4 or 1,3,5 we can compute L. Furthermore, given any three areas we can compute L, because to avoid having any of the sufficient pairs we must have one from each pair, and hence we have two from one triple and one from the other. Combining the triple with one unknown with the double with the same unknown, we can solve for L. Once we have L, we can then compute x and y using any pair of the individual area equations (adjusting θ if necessary). The distance from the center of the hexagon to the intersection point can be found by writing (1) in the form

We have taken θ = 0 but the result goes through with arbitrary θ. Squaring both sides and summing over n = 0 to 5 gives

The sums of the squares cosines and of the squared sines are both 3, and the cross term summation vanishes, so we have

where <A> = L²√3 is one sixth of the total area of the hexagon. As a check, note that if each region’s area equals A^*, each term in the right hand summation vanishes, consistent with the fact that the intersection point is at the center of the hexagon in that case.

In general, for an N-sided regular polygon with lines drawn from the midpoints of the edges to some intersection point, and the signed areas (indexed 1 to N) of the quadrilaterals are

where R is the distance from the center of the polygon to a vertex. The distance D from the intersection point to the center of the polygon is given by

where <A> is the average of the individual A_j values, meaning it is 1/N times the total area of the polygon, i.e., we have

For even N the value of R can be inferred from any pair of areas on opposite edges. We can also write this relation as

The quantity in the square brackets is the variance of the set of areas.

Noting that x = Dcos(α) and y=Dsin(α) for the angle α between the positive x axis and the line from the origin to the intersection point, equation (2) can be re-written in the form

For any two (non-opposite) regions with areas A_i and A_j and angles to the respective vertices θ_i and θ_j, we can eliminate α from these two equations to give

where

For opposite regions with |θ_i − θ_j| = π this doesn’t apply, because in this case the denominator is zero and A_i + A_j = 2<A>, so D drops out and the identity reduces to 2K_iK_j/(K_i² + K_j²) = −1.

To determine the values of <A> and R and x and y it suffices to specify three of the individual areas A_i, A_j, A_k. Choosing any two non-opposite of these, say A_i and A_j, we have by (2) the relations

Solving these for x and y gives

Substituting these into the third relation of the form (2) gives

Thus we have

Replacing the K values with their definitions, this gives the result

From this we can directly compute the values of R, x, y, and all the other individual A_n values.

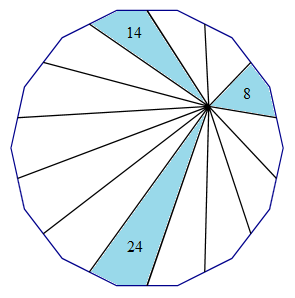
As an example, consider the regular tetradecagon (14-sided polygon) shown below, partitioned into 14 quadrilateral regions by lines drawn from the midpoints of the edges to a particular focus point.

The areas 8, 14, and 24 of three of the regions are specified, in units of squared length. Based on this information, what is the total area of the tetradecagon? Using the formula for <A>, we can compute the total area as

The radius R of the circumscribing circle is

Likewise we can easily compute the x and y coordinates of the focus point (for the configuration shown), the distance of this point from the center of the tetradecagon, and the individual areas of all the other regions.

Return to MathPages Main Menu