Triangles in a Row

As you from crimes would pardoned be,

Let your indulgence set me free.

Consider n+1 copies of an arbitrary triangle placed in a row as shown below for the case n=4.

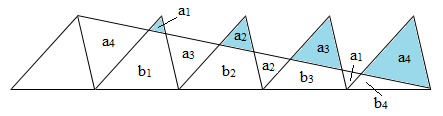
Now we draw a line from the top vertex of the left-most triangle to the lower-right vertex of the right-most triangle, and we shade the portions of the triangles above this line, as shown below.

We’ve denoted the areas of the various regions by a_j and b_j. Given that each of the original n+1 triangles has area A, what is the total area of the shaded regions above the line?

By similar triangles it’s immediately apparent that the edges of the triangular regions a_j are in proportion to j so the areas are in proportion to j², and hence we have a_n = n²a₁. Also, the triangle whose edges are the diagonal and the bases of the right-most n original triangles has area nA (being half the parallelogram with area 2nA, and also by altitude and base), and this equals n² times the area of the similar triangle with area b_n + a₁. Thus we have the two relations

Solving these equations for a₁ gives

The well-known sum of squares from 1² to n² is n(n+1)(2n+1)/6, so we have

This problem is often posed for equilateral triangles, but (as shown above) the same result applies to triangles of any shape.

Return to MathPages Main Menu