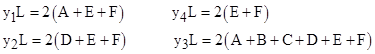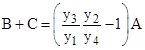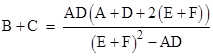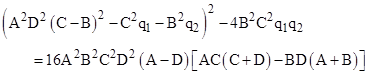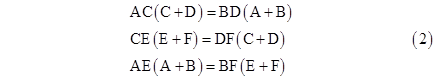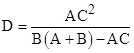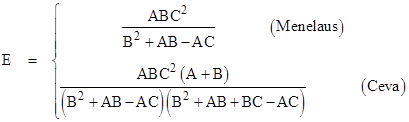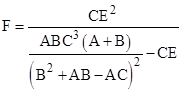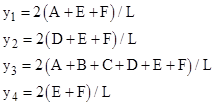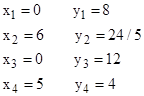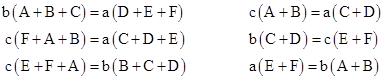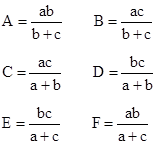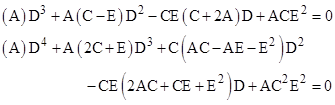Areas of Triangle Partitions

Oh as I was young and easy in the mercy of his means,

          Time held me green and dying

     Though I sang in my chains like the sea.

                                      Dylan Thomas

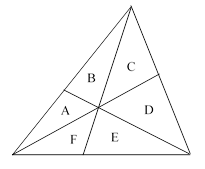
Suppose we partition an arbitrary triangle into six parts by lines from the vertices to the opposite edges, intersecting at some arbitrary internal point, as shown below.

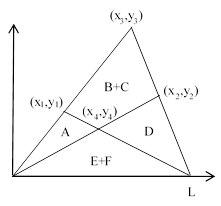
The symbols A, B, …, F denote the areas of the respective regions. Several relationships between these areas can be deduced.  For example, given the values of A, D, and E+F we can compute the values of B and C. This can be depicted in terms of coordinates as shown below.

Obviously by simple proportions we have x₁y₃ = y₁x₃ and x₂y₄ = y₂x₄. Likewise we have

Noting that

and making the substitutions x₃ = y₃(x₁/y₁) and x₄ = y₄(x₂/y₂) in the previous expressions we have

Consequently we have

By inspection we also have the ratios

(As an aside, note that the values of the upper x coordinates are not uniquely determined, since we can slide those vertices horizontally on the base L without affecting the areas.) Inserting these expressions in the previous equation, solving for B+C, and simplifying, we get the result

Similarly we can derive the following expressions for the individual values of B and C:

Solving each of these for E+F we get

where q₁ = A²D² + 4ABD(A+B) and q₂ = A²D² + 4ACD(C+D). Isolating the radicals and successively squaring, we arrive at

The vanishing of the quantity in square brackets gives the relations

Equating the product of the left sides with the product of the right sides, we get the nice relation (ACE)² = (BDF)² and hence

With the plus sign this is essentially equivalent to Ceva’s Theorem, since the ratio of the areas of adjacent regions on the same edge equals the ratio of their bases. Note that another root of the squared quadratic expression is with A=D, in which case it follows that B=C and hence E=F.

Given the areas of any three of the regions, equations (2) enable us to find the areas of the remaining regions. The form of the constraints depends on which three areas are given. For example, if we are given the areas A, B, and C, we can use the first of equations (2) to compute D as

and substitute this into the second and solve for F in terms of A, B, C, and E. We can then substitute this into the third relation in (2) to give a quadratic in E, which has two linear factors, yielding the two possible values

We refer to these two solutions as Menelaus and Ceva for the reason explained later. For either of these E values, the corresponding value of F is given by

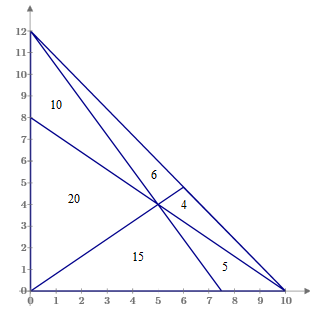
For example, with A=20, B=10, and C=6 we can compute D=4, E=5, F=15 for the Ceva case, and we get D=4, E=10, F=−30 for the Menelaus case. To draw the Ceva case, we have the y coordinates

As noted above, the x coordinates of the vertices are ambiguous, but for convenience we can set x₁ = x₃ = 0 to give

The value of L is also ambiguous, noting that larger L results in smaller y values and larger x values. Choosing L = 10, we get the coordinates

This configuration is depicted in the figure below.

The three ratios of the areas on the same edge can be expressed in terms of three parameters a,b,c as A/B = b/c, C/D = a/b, and E/F = c/a, consistent with the fact that (ACE)/(BDF) = 1. The same ratios apply to other combinations of triangles on the same edges, since they have equal altitudes and the areas are proportional to the bases. Thus we have the simple cyclic ratios

Only two of the three right hand conditions are independent, but when combined with the requirement for the sum of all the areas to be 60, these conditions suffice to uniquely determine the values of the individual areas. Hence we have a three-parameter solution to equations (2):

With a=3, b=2, c=1 this gives (up to a scale factor) the integer solution depicted above. Noting that A+B = a, C+D = c, and E+F = b, we can also easily answer questions such as the one at the beginning of this article, in which the values of E+F, A, and D are specified, which immediately gives us the value of b = E+F and two linear equations in a and c which can be solved to give a = Ab(D+b)/(b² – AD) and c = Db(A+b)/(b² – AD). This yields the same values for B and C as given previously.

There is an interesting ambiguity when the three given areas are for a set of alternating regions, such as A, C, E. In that case we must use all three of the relations (2) to simultaneously solve for B, D, F. The equations are non-linear, and if we eliminate B and F, we get the single polynomial of degree 7 in the unknown D that factors into a cubic and a quartic polynomial, the vanishing of either of which leads to a solution. Thus the solutions are the roots of either of the equations

As an example, suppose we are given A=3, C=18/5, E=7/4. With these values the quartic polynomial has the root D=2, from which we can compute B=21/5 and F=9/4. We can verify that Ceva’s theorem ACE=BDF is satisfied. But there are six other roots of these polynomials. The other six roots of the quartic and cubic lead to one or more of the areas being negative. In those cases we appear to be dealing with Menelaus’ theorem, corresponding to the relation ACE = −BDF. In geometrical terms, it’s tempting to think that the 7 roots correspond to solutions with the “crossing point” located in each of the seven regions of the plane bounded by the extended edges of the triangle as depicted below.

The “Ceva configurations” are those for which the crossing point is in the interior of the triangle denoted as region “1”. An example of a “Menelaus configuration” with the intersection point outside the original triangle is shown below.

In our example, we chose the root D=2, but another root gives D = 0.7740107994…, from which we can compute B = 6.4549894622… and F = −3.7828510965…, which satisfies the Menelaus condition ACE = −BDF.

Return to MathPages Main Menu