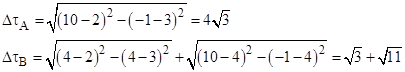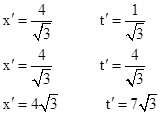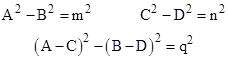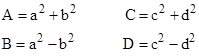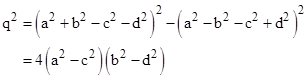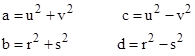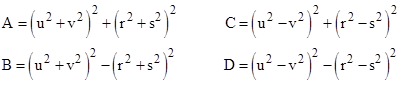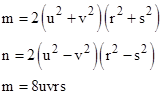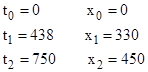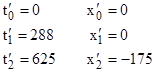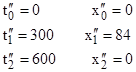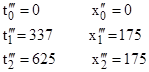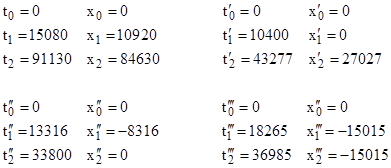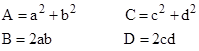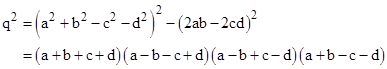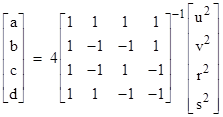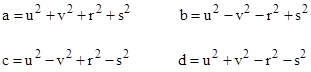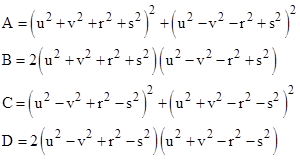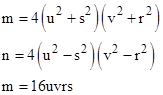Rational Triangles in Space-Time

This story shall the good man teach his son;

And Crispin Crispian shall ne'er go by,

From this day to the ending of the world,

But we in it shall be remember'd…

                                    December 14, 2009

To describe the effect of time dilation and the invariance of elapsed proper time in special relativity, one often sees examples such as this:

In terms of a specified system of inertial coordinates (with units so c=1), two ideal clocks, A and B, coincide at x=3,t=2.  Clock A moves inertially from there to x=–1,t=10, and clock B moves inertially to x=4,t=4, and from there it moves inertially to x=–1,t=10.  How much time has elapsed on A and B between when they separate and when they are reunited?

Obviously the elapsed proper times are

This simple result involves square roots, which may be distracting to students who are not comfortable with irrational numbers. The multiple equivalent ways of expressing the same value, such as √48 = 4√3 = 12/√3 seem to confuse some students. Furthermore, to illustrate the invariance of these elapsed proper times under Lorentz transformations, we may wish to convert the coordinates to a system x′,t′ in which the first leg of clock B is stationary, and this typically introduces more surds. Since the first leg goes from (x=3,t=2) to (x=4,t=4), we know that v=1/2, so we can apply the Lorentz transformation x′=(x–vt)γ, t′=(t–vx)γ with v=1/2 and γ=1/√(1–v²).  The coordinate for the three relevant events are

As expected, the x′ coordinates for the first two events are equal, because that leg is stationary in terms of this system of coordinates. Also, it is easily verified that the elapsed proper times are unchanged. Naturally we can similarly transform to any other system of coordinates we like, and always get the same elapsed times.

However, numerical examples such as this suffer from the square roots, making the expressions look unnecessarily complicated. Can we give examples of this kind that involve only integers for the coordinates and the elapsed proper time?

For convenience, take one of the events at the origin, x₀=0, t₀=0, and consider time-like inertial world lines from the origin to the events t₁=A, x₁=B and t₂=C, x₂=D, which we can choose to be integers. The elapsed proper times for the three intervals from event 0 to event 2 and for the segmented path from event 0 to event 1 and from event 1 to event 2 will all be integers just if

for integers m, n, and q. Using the Euclidean formula for Pythagorean triples, we can ensure the first two conditions by setting

for arbitrary integers a,b,c,d, which will yield the integer values m = 2ab and n = 2cd. The third condition is then satisfied just if

This will be satisfied if each of the quantities in parentheses in the last expression is a square, so we can use the Euclidean formula again to set

for integers u,v,r,s. Hence if we set

then the elapsed proper times represented by m,n q will have the integer values

As an example, suppose we arbitrarily set u=1, v=2, r=1, and s=3. With these values we have A = 125, B = –75, C = 73, D = –55. From this we get m = 100, n = 48, and q = 48. For later convenience we will multiply all these values by 6, and swap the positive and negative x directions, to give the purely integer coordinates for three events

Letting τ_ij denote the elapsed proper time for the inertial path from event i to event j, we have

Thus the elapsed time for the total path from event 0 to event 1 to event 2 is 576, which is less than the elapsed time of 600 for the inertial path directly from event 0 to event 2.

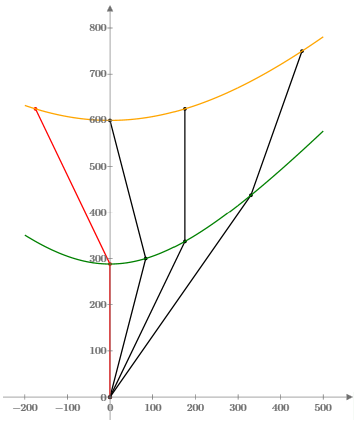
The first leg of the segmented path has speed v = 55/73 in this frame. Applying the Lorentz transformation for this speed, the transformed coordinates are

Similarly we can transform to inertial coordinates x″,t″ in which the world line from event 0 to event is 2 is stationary. Using the relevant velocity v = 75/125 = 3/5, we get

In terms of a system of inertial coordinates x‴,t‴ in which the interval from event 1 to event 2 is stationary, the coordinates of the three events are

The figure below shows these three events in terms of the four different systems of coordinates.

For another example, we can set u=1, v=3, r=4, and s=6. With these values we have A = 2804, B = –2604, C = 464, D = –336. From this we get m = 1040, n = 464, and q = 576. We can clear the fractions that arise later by multiplying by 65/2. Also we again swap the positive and negative x directions, to give the purely integer set of events

with the elapsed proper times

A slightly different approach is to make the alternative identification of the terms of the Euclidean formula for Pythagorean triples by setting

for arbitrary integers a,b,c,d, which will yield the integer values m = a² – b² and n = c² – d². The third condition is then satisfied just if

The right side will be a square if each of the factors is a square, so suitable values of a,b,c,d can be given by the following (where we’ve inserted a factor of 4 to ensure integer values)

for arbitrary integers u,v,r,s. Thus we have

Hence if we set

then the elapsed proper times represented by m,n q will have the integer values

For example, setting u=1, v=3, r=4, and s=6, as in our previous example, we get A=916, B=240, C=500, D=400, and from this we get m = 884, n = 300, and q = 384.

Return to MathPages Main Menu