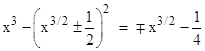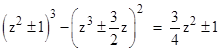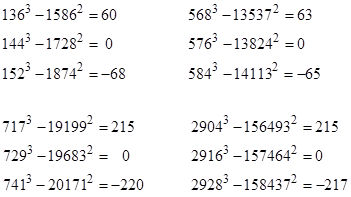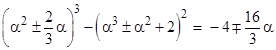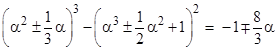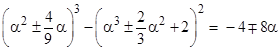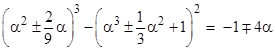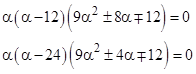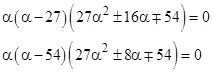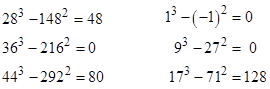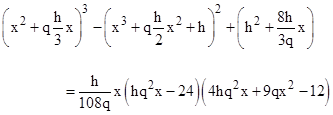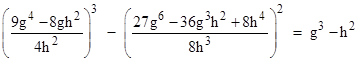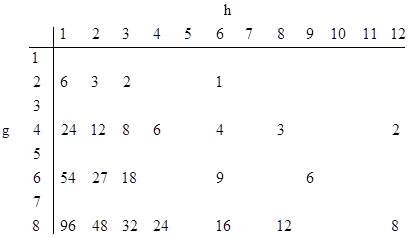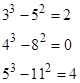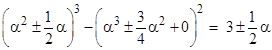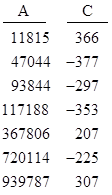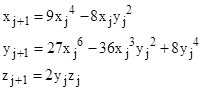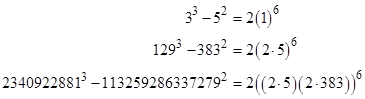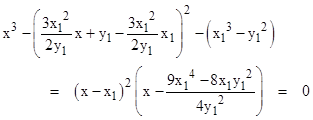Squares Close to Cubes

Any sixth power is both a square and a cube, but there are also squares that are close, but not exactly equal to, cubes. Some familiar examples are

A few examples in slightly larger numbers are

In general we can define the function

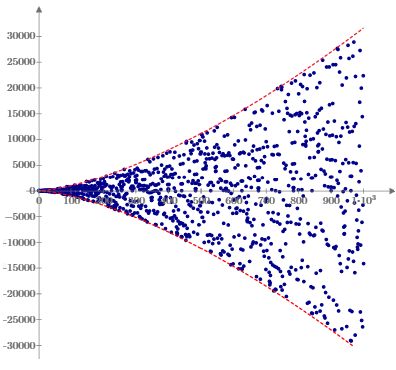
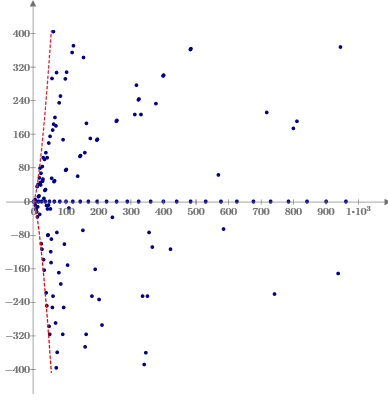
Obviously f(y²) = 0 for every integer y. We seek integer values of x for which f(x) is small but non-zero. The figure below show the values of f(x) for all integers x up to 1000.

The maximum magnitudes occur when x^3/2 is half way between two integers, resulting in a shift of 1/2, so the envelope of values (denoted by the dashed curves) is given by

Even though the envelope increases as the 3/2 power, we can find an infinite family of values that increase only linearly, based on the algebraic identity

This shows that for every even integer z = 2n there are two adjacent integer solutions of A³ – B² = C such that C is approximately equal to (3/4)A.

Among the other solutions, we find some interesting “symmetrical sets” of inter-related solutions. These sets consist of two near-solutions that occur symmetrically on either side of an exact solution. The four most obvious examples are summarized below:

To construct two inter-related examples of the form A³ – B² = C we might begin with numbers A = α² and B = α³, so they satisfy A³ = B², and then try to adjust these in a symmetrical way to give slightly non-zero differences. The first example set is given by putting α = 12 in the signed expressions

The second set is given by setting α = 24 (twice the previous value) in the expressions

This is in a way the most striking example, because we have the additional symmetry

Coincidentally, the two values of “B” are consecutive “star numbers”, given by 6n(n–1)+1 with n = 48 and 49.

The third set corresponds to the two equalities with α = 27 in the signed expressions

Lastly, the fourth set corresponds to the fact that with α = 54 (twice the previous value) we have the two equalities

Of course, the expressions above are not algebraic identities, they are just equalities for the specified values of α. For example, the expressions for α = 12 and α = 24 are algebraically satisfied if and only if

respectively, confirming that in each case the respective value of α gives a solution for both of the alternatively signed expressions, as does α = 0 (trivially). In each case there are also four solutions (allowing for choice of signs) involving radicals based on the roots of the quadratic factor.

Likewise the expressions for α = 27 and α = 54 are algebraically satisfied if and only if

respectively. These factorizations show that the relationship between these two pairs of solutions are very similar. Since the solution pairs seem to occur at half values, we expect that we could extend the family with α = 24 and α = 12, to find solutions for α = 6 and α = 3 of this same form. Extrapolating the pattern of expressions for the equalities and factorizations, we find

These pairs have the same formal symmetry even though it is not as apparent numerically. From this we find that the equalities for all the pairs (except for the self-dual example) can be traced to the algebraic identity

The equalities for the cases α = 24, 12, 6, and 3 correspond to q = ±1 and h = 2ⁿ where n = 0, 1, 2, and 3 respectively.  Likewise the equalities for the cases α = 54 and 27 correspond to q = ±2/3 and h = 2ⁿ where n = 1 and 2 respectively. More generally, if we set x = 24/(hq²) so that the right side of the above identity vanishes, and we define the parameter g = –4/q, we get the two-parameter family of identities

(This is equivalent to Bachet’s duplication formula for the elliptic curve h² – g³ = c.) The family of α = 24, 12, 6, 3 has the parameters g = 4 and h = 1, 2, 4, and 8 respectively. The family α = 54, 27 has the parameters g = 6 and h = 1, 2 respectively. Integer values of α = 3g²/(2h) for various values of g and h are shown in the table below.

Of course, these integer solutions do not in general give small values of C/A, but the formula does enable us to construct solutions with arbitrarily low values of that ratio. For example, if we put g = 2n and h = 1 we get the identity

Thus the values of C/A approach 2/(9n) as n increases.

As an aside, there is a somewhat similar example of a symmetrical set

This example can be expressed by the two equalities with α = 2:

Again, this is not an identity, it is satisfied if and only if

This self-dual solution doesn’t fit into the pattern of the other symmetrical sets.

Focusing on just solutions of A³ – B² = C with |C| less than 400, the plot below shows that there is more regularity in the solutions with positive C than with negative C. For example, the infinite family of pairs adjacent to even square values of A all have positive C.

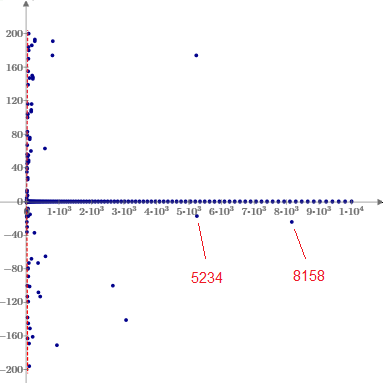
Extending the range of A values of up 10000 and narrowing the focus to C values less than 200, we see that solutions become quite rare, but still occur.

The two unusually low solutions shown here are

Coincidentally, there are three other (much smaller) examples of cubes minus squares are equal to –17, namely

The next smaller value of A below 5234 for which the magnitude of C is less than 25 is just 109, and there are no known values of A greater than these for which C has magnitude less than 200. There are, however, several values of A for which |C| is less than 400, as listed below.

The two-parameter identity derived above can be used to generate infinitely many integer solutions of Diophantine equations of the form x³ – y² = kz⁶ for certain values of k (including 2, 4, 7, 11, 13, … and negative values including –8, –9, –12, –15, –17…). Multiplying through the two-parameter identity by (2h)⁶, we can clear the denominators, which leads to the result that for any initial integer values x₀, y₀ with z₀ = 1 we have

where

For example, beginning with x₀ = 3, y₀ = 5 we have for the Diophantine equation x³ – y² = 2z⁶ the infinite family of solutions

and so on. Incidentally, starting with x₀ = 2, y₀ = 3 we have the initial relation 2³ – 3² = –1(1)⁶, so it might seem as if we can generate counter-examples to the theorem that there are no non-trivial integer solutions of x² + y³ = z⁶. However, these initial values give x₁ = 0, and hence all subsequent values of x_j are zero, yielding just the trivial solutions.

The usual way of deriving the duplication formula for the elliptic curve y² = x³ – c is to consider the intersection between this curve and a line y = ax + b that is tangent to the curve at some rational point x₁,y₁. Taking the derivative of the elliptic curve gives 2ydy = 3x²dx, so we have a = 3x₁²/(2y₁) and hence b = y₁ – ax₁. Substituting the linear expression for y into the equation of the elliptic curve and re-arranging terms (putting c = x₁³ – y₁²) gives

Thus two intersections occur at the tangent point and the third is the rational point given by the duplication formula. Using this same approach, given any two rational points on the curve we can construct a third rational point.

Return to MathPages Main Menu